自变量为定类数据的多元线性回归分析，哑变量转化与分析

线性回归因变量须是定量数据，自变量允许是定量数据或定类数据。定类数据中，如果是二水平的分类变量一般视为定量数据，可直接进行线性回归。而对于多个分类水平的分类自变量，应酌情考虑将其转换为哑变量，以哑变量的形式参与线性回归分析。

1. 哑变量转换

例如A、B、AB、O四种血型数据，依次用数字1、2、3、4表示，如果直接以血型作为自变量，则回归系数表示血型每增加/减少一个单位，因变量随之增加/减少的改变量，这与实际情况不符，因为四种血型是平等的关系，并不存在递增或递减的效应。遇到此类自变量的线性回归分析，应考虑将分类变量转换为数个哑变量，每个哑变量只代表与参考水平相比的差异，这样做所得回归系数才有实际意义。

哑变量，又称为虚拟变量，它是人为虚设的变量，所以有些地方也称之为虚设变量。哑变量最常见的表示方式是“指示符法”，即用用0-1数据进行组织。

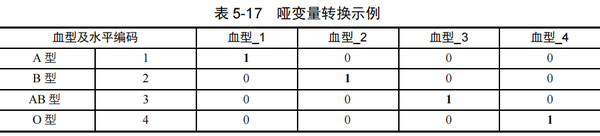
一个有k个水平的多分类变量转换为哑变量时，可生成k个哑变量，每个哑变量均为0-1数据，1表示原分类水平的一个分类，0表述非此类。

如表5-17所示，哑变量“血型_1”的编码1对应的是“A型”，编码0则表述“非A型”，该哑变量代表的就是“A型”血型；哑变量“血型_2”则对应“B型”；哑变量“血型_3”则对应“AB型”；哑变量“血型_4”则对应“O型”。同一个分类变量转换所得的多个哑变量，一般简称为“一组”或“一簇”哑变量。

再SPSSAU平台中，可通过【数据处理】→【生成变量】模块对多分类的自变量进行哑变量处理，相关介绍见本书2.4节的内容。

2. 参照水平

多分类变量转换为哑变量参与线性回归时，应选择一个恰当的分类作为参照水平，即哑变量回归时，纳入回归模型的哑变量为k-1个，减掉的这一个作为参照。例如，我们可选择“O型”作为参照，此时参与回归的仅包括“血型_1”、“血型_2”、“血型_3”这三个哑变量，而哑变量“血型_4”作为参照不纳入回归模型。

哑变量回归时，应注意遵守“同进同出”原则。即任意一个哑变量对因变量Y有显著性，则同组哑变量均一并纳入回归模型；一组哑变量对因变量Y无显著性，则该组哑变量全部踢出模型。

值得注意的是，参照水平的选择不是随意的。主要根据专业和研究目的(冯国双，2018)。怎么理解呢？比如研究目的在于考察“吸烟”对患某疾病的影响研究，则以“不吸烟”作为参照；再比如研究病情严重程度对预后质量的影响，根据专业知识病情严重程度划分为4个等级，则可考虑将等级最低的水平作为参考，有利于临床意义的解释。

3. 实例分析

【例5-7】对“例5-1”案例背景和数据进行重新整理，数据文档为例“例5-7.xls”。某研究收集到757名美国年轻男子的数据，行业经验认为“年龄”、“教育年限”及“智商等级”对“Ln_工资”的对数数据有预测作用，试拟合多重线性回归进行分析。

1) 哑变量转换

本例“智商等级”为有4个分类水平的分类变量，4个等级数字编码依次为1、2、3、4。其作为线性回归自变量时，考虑对其进行哑变量转换生成3个哑变量，以3个哑变量的形式参与线性回归。

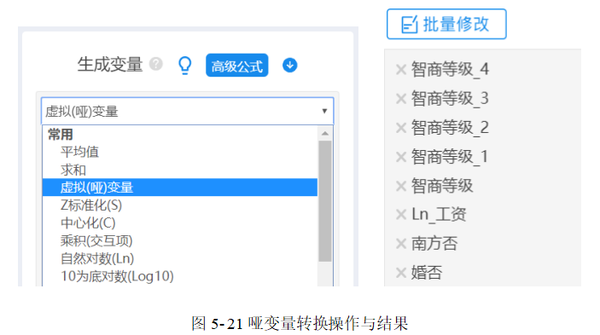
依次选择【数据处理】→【生成变量】模块，先在左侧的变量列表中选中“智商等级”，然后在右侧【生成变量】功能下拉框内选择常用的【虚拟(哑)变量】功能，最后单击底部的【确认处理】，操作设定如图 5-21所示。转换后，原始数据中新增“智商等级_1” ～“智商等级_4”4个哑变量，分别对应的是“智商等级”的四个水平。此处应注意，应选择其中一个水平作为参照，本例选择“智商等级_1”即第一个水平作为参照，其余三个哑变量参与接下来的线性回归。

2) 线性回归

同一组哑变量应同步进入模型或同步退出模型，为此哑变量不适合按照逐步回归的方式进行筛选，本例选择使用【线性回归】模块完成线性回归分析。依次选择【通用方法】→【线性回归】模块，如图 5-22所示，将量“Ln_工资”拖拽至【Y(定量)】，“年龄”与“教育年限”拖拽至【X(定量/定类)】。

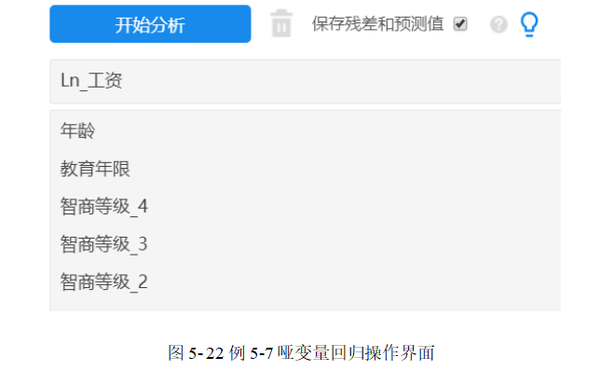
本例以“智商等级_1”为参照，将“智商等级_2” ～“智商等级_4”这三个哑变量拖拽至【X(定量/定类)】。勾选【保存残差和预测值】，最后单击【开始分析】。

3) 结果分析

首先来看线性回归结果，如下表5-18所示。

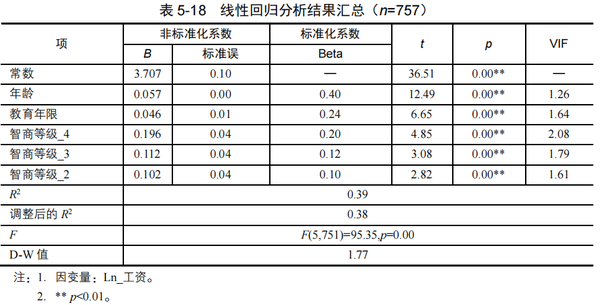
(1) 回归方程总体显著性检验，F(5,751)=95.35，p﹤0.01，按α=0.01水平，认为本次拟合所得的回归方程具有统计学意义。

(2) 偏回归系数检验，“年龄”和“教育年限”2个自变量，以及智商等级的3个哑变量，t检验p值全部小于0.01，说明这5个自变量对“Ln_工资”的影响有统计学意义。相对于“智商等级_1”来说，由智商等级_1变换到等级_2，工资水平增加10%；等级_1变换到等级_3，工资水平增加11%；等级_1变换到等级_4，工资水平增加20%，可见智商对工资的影响。

(3) 最终回归方程为：

Ln_工资=3.707 + 0.057×年龄 + 0.046×教育年限 + 0.196×智商等级_4 + 0.112×智商等级_3 + 0.102×智商等级_2

(4) 模型拟合评价，回归方程调整后R方=0.38，表示“Ln_工资”变异的38%能被上述多重线性回归方程所解释。

以上内容摘自《SPSSAU科研数据分析方法与应用》第5章——相关影响关系研究，书中不仅涵盖了数据清理、统计分析和模型构建等内容，还提供了丰富的案例，以便于读者在实际研究中应用。