通过Julia求解非线性方程和常微分方程

方程求根

二分法

对于方程$f(x)=0$，如果$f(a)\cdot f(b)<0$，则说明$a,b$之间必有根，如果按照某个步长对其进行搜索，那么最终一定能够不断缩小根的取值范围，不断精确化。

二分法就是基于这种思想的一种算法，其实质是对区间进行快速选取。如果已知$f(a)\cdot f(b)<0$，则快速选取$c=\frac{a+b}{2}$，如果$f(a)\cdot f(c)<0$，则说明根在$(a,c)$之间，否则即说明根在$(a,b)$之间，然后不断第迭代下去。

# equations.jl
# 二分法求根，f为函数，err为误差
# 要求f(a)*f(b)<0
function Dichotomy(f,a,b,err)
    c = (a+b)/2
    val = f(c)
    #如果f(c)和f(a)异号，则将c赋值给b，否则将c赋值给a
    val*f(a)<0 ? b=c : a=c
    #如果大于误差，则继续二分，否则输出c
    return abs(val)>err ? Dichotomy(f,a,b,err) : c
end

验证

julia> include("equations.jl");
julia> f(x) = x^5+x^4+x^2+1;
julia> x = Dichotomy(f,-2,1,0.01);
julia> f(x)
0.009531426464285175

Newton法

如果$f(x)$=0可以写成$x=\phi (x)$的形式，则可以将这个方程的根理解为$y=\phi (x)$与$y=x$的交点。现给定一个初值$x_0$，将其代入$\phi (x)$中，则$\phi (x_0)$对应一个新的$x$，记为$x_1$。

如果数列 { x n } \{x_n\} {xn​}收敛，那么必有$x={\lim }_{k\to \infty }{x}_k$即为方程的根。所以，问题的关键在构造合适的$\phi (x)$使得数列能够快速收敛。

其最简单的形式莫过于$x_{k+1}=x_k+f(x_k)$，不过这种迭代公式看起来十分危险，如果$f(x_k)是一个大于0的单调递增函数，那么结果就爆炸了。

所以，最好为$f(x_k)$乘以一个系数，当$f(x_k)$增加时使之变小，当其递减时使之变大。所以一个比较好的形式为

$$x_{k+1}=x_k-\frac{f(x_k)}{f^{\prime }(x_k)}$$

此即Newton公式。

除了迭代形式，Newton公式也可以作为二分法的一个升级版本，$x_k-\frac{f(x_k)}{f^{\prime }(x_k)}$可以表示过$(x_k,f(x_k))$做切线与$x$轴的交点，通过切线选取新的$x$值取代了二分法的盲动性。

其Julia实现为

# Newton法
# f为函数，x为初始值，err为误差
function Newton(f,x,err)
    fx = f(x)
    df = (fx-f(x-err))/err      #近似斜率
    xNew = x-fx/df

    # 如果满足精度要求则返回，否则继续迭代
    return abs(xNew-x) > err ? Newton(f,xNew,err) : xNew
end

验证

julia> include("equations.jl");
julia> f(x) = x^5+x^4+x^2+1;
julia> x = Newton(f,1,0.01);
julia> f(x)
-0.0028617855019934524

常微分方程

Euler方法

一阶常微分方程的一般形式为

$$\{\begin{array}{rl}\frac{\text{d}y}{\text{d}x}=& f(x,y)\to \text{d}y=f(x,y)\text{d}x\\ y(x_0)=& y_0\end{array}$$

如果将$x$划分为一系列子区间，其端点序列为$x_0,x_1,\dots ,x_n$，则上式可写为

$$\begin{array}{rl}\text{d}{y}_n=& f(x_n,y_n)\text{d}{x}_n\\ \to y_{n+1}=& y_n+f(x_n,y_n)\text{d}{x}_n\end{array}$$

此即$\text{Euler公式}$，记$f_n=f(x_n,y_n),h=d{x}_n$，则可更加简洁地写为

$$y_{n+1}=y_n+f_{n}h$$

在已知初值的情况下，可以递推地计算出此后的函数值。

# Euler法
# f为dy/dx=f(x,y), x为输入区间，n为步长
function Euler(f,x,y0,n)
    h = (x[2]-x[1])/n
    x = [x[1]+i*h for i in 1:n]
    y = zeros(n)
    y[1] = y0
    for i in 2:n
        y[i] = y[i-1]+h*f(x[i],y[i-1])
    end
    return y
end

验证

julia> include("equations.jl")        
julia> f(x,y) = y-2*x/y     #导函数
julia> Y(x) = sqrt(1+2*x)   #原函数
julia> x = [0,1]            #区间
julia> y0 = 1
julia> yEuler = Euler(f,x,y0,100);
julia> X = [i for i in 0.01:0.01:1]
julia> yReal = Y.(X)
julia> using Plots
julia> plot(X,[yEuler,yReal],st=[:line :scatter])
julia> savefig("naiveEuler.png")

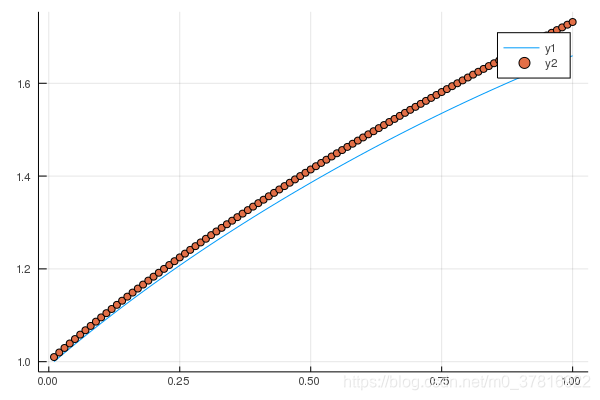
如果对于[0,1]区间，我们给的初值为$y(1)=y_1$，那么其求解过程将变成从后向前的运算，公式$y_{n+1}=y_n+f(x_n,y_n)\text{d}{x}_n$也将从显式变成隐式，因为此时的$y_n$将是一个未知量。

这种隐式的Euler公式即为Euler公式的后退格式，如果想要将其改为从前向后的计算风格，即可写为

$$y_{n+1}=y_n+f(x_{n+1},y_{n+1})\text{d}{x}_n$$

如果同时考虑前向格式和后向格式，那么可以将二者综合为

$$y_{n+1}=y_n+(f_n+f_{n+1})\frac{h}{2}$$

此即Euler公式的梯形格式，这仍然是一个隐式，所以需要对其进行迭代求值，在给定初值的情况下，有

$$\{\begin{array}{rl}{y}_{n+1}^{(0)}=& y_n+hf(x_n,y_n)\\ y_{n+1}^{(k+1)}=& y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_{n+1}^{(k)})]\end{array}$$

这个算法在处理每个点时，都需要进行大量的迭代，开销很大，但实现过程并不复杂，只需对原始的Euler公式稍加改进即可

# Euler法
# f为dy/dx=f(x,y), x为输入区间，n为步长
# nIter 为梯形格式的迭代次数
function Euler(f,x,y0,n,nIter)
    h = (x[2]-x[1])/n
    x = [x[1]+i*h for i in 1:n]
    y = zeros(n)
    y[1] = y0
    for i in 2:n
        y[i] = y[i-1]+h*f(x[i],y[i-1])
        for j in 1:nIter
            y[i] = y[i-1]+h*f(x[i],y[i])
        end
    end
    return y
end

当迭代次数为1时，被特别称为改进的Euler法。

$$\{\begin{array}{rl}{y}_{test}=& y_n+hf(x_n,y_n)\\ y_{n+1}=& y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_{test})]\end{array}$$

Runge-kutta法

Runge-Kutta法是一种高精度的单步法，其根源是$Tylor$公式：

$$y(x_{n+1})=y(x_n)+h{y}^{\prime }(x_n)+\frac{h^2}{2!}{y}^{\prime \prime }(x_n)+\frac{h^3}{3!}{y}^{\prime \prime }(x_n)+\dots$$

其中导数之间存在递推关系

$$\{\begin{array}{rl}{y}^{\prime }=& f,\\ y^{\prime \prime }=& \frac{\partial f}{\partial x}+f\frac{\partial f}{\partial y}\\ y^{\prime \prime \prime }=& \frac{{\partial }^{2}f}{\partial x^2}+2f\frac{{\partial }^{2}f}{\partial x\partial y}+f^2\frac{{\partial }^{2}f}{\partial y^2}+\frac{\partial f}{\partial y}(\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y})\\ ⋮& \end{array}$$

Euler法截取了一阶Taylor公式作为拟合方程，如果提高Taylor格式的阶数，将有助于计算结果精度的提高。

现假设有一点$p\in (x_n,x_{n+1})$，且$x_p=x_n+ph,p⩽1,h=x_{n+1}-x_n$。设$x_n,x_{n+1}$点的斜率分别为$K_1,K_2$，则$\frac{y_{n+1}-y_n}{h}$可以表示为$K_1,K_2$的线性组合，即

$$y_{n+1}=y_n+h({\lambda }_1{K}_1+{\lambda }_2{K}_2)$$

由于$x_n$点是暴露给我们的，我们可以设$K_1=f(x_n,y_n)$，并且通过$K_1$来估测$x_p$处的值，即$x_p$处的函数值为$F(x_p)=y_n+K_{1}ph$，从而可以得到$K_2=f(x_p,y_n+K_{1}ph)$。

对$K_2$进行展开可以得到

$$\begin{array}{rl}{K}_2=& f(x_n+ph,y_n+ph{K}_1)=f(x_n,y_n)+\frac{\partial f}{\partial x}\text{d}x+\frac{\partial f}{\partial y}\text{d}y\\ =& f(x_n,y_n)+f_x(x_n,y_n)ph+f_y(x_n,y_n)ph{K}_1\\ \stackrel{K_1=f(x_n,y_n)}{\Rightarrow }& f(x_n,y_n)+ph(f_x(x_n,y_n)+f_y(x_n,y_n)f(x_n,y_n)\end{array}$$

这正与Taylor展开式有相同的形式，将$K_1,K_2$代入$y_{n+1}=y_n+h({\lambda }_1{K}_1+{\lambda }_2{K}_2)$，则可得到

$$\{\begin{array}{r}{\lambda }_1+{\lambda }_2=1\\ {\lambda }_{2}p=\frac{1}{2}\end{array}$$

在此条件下，可整理得出二阶Runge-Kutta的表达形式

$$\{\begin{array}{rl}{y}_{n+1}=& y_n+h({\lambda }_1{K}_1+{\lambda }_2{K}_2)\\ K_1=& f(x_n,y_n)\\ K_2=& f(x_p,y_n+ph{K}_1)\end{array}$$

通过Julia写为

# Runge-Kutta法，p取1/2
# f为dy/dx=f(x,y), x为输入区间[x1,x2]，n为步长
function RungeKutta(f,x,y0,n)
    h=(x[2]-x[1])/n
    x = [x[1]+i*h for i in 1:n]
    y = zeros(n)
    y[1] = y0
    for i in 2:n
        K1 = f(x[i-1],y[i-1])
        K2 = f(x[i-1]+h/2,y[i-1]+h*K1/2)
        y[i] = y[i-1]+h*K2
    end
    return y
end

验证其验证过程与Euler法完全相同，甚至连保存的图片都几乎一致，只需把Euler函数换为RungeKutta即可。

结合Taylor公式可知，二阶Runge-Kutta法绝非优化的极限，我们可以通过进一步增加参数，来拟合Taylor公式中的高阶项，于是有了更高阶的Runge-Kutta法。

由

$$y^{\prime \prime \prime }=\frac{{\partial }^{2}f}{\partial x^2}+2f\frac{{\partial }^{2}f}{\partial x\partial y}+f^2\frac{{\partial }^{2}f}{\partial y^2}+\frac{\partial f}{\partial y}(\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y})$$

若三阶Runge-Kutta项的形式为

$$\begin{array}{rl}{y}_{n+1}=& y_n+h({\lambda }_1{K}_1+{\lambda }_2{K}_2+{\lambda }_3{K}_3)\\ K_1=& f(x_n,y_n)\\ K_2=& f(x_p,y_n+ph{K}_1)\\ K_3=& f(x_n+qh,y_n+qh(r{K}_1+s{K}_2))\end{array}$$

则可推导出各参数所需要满足的条件

$$\{\begin{array}{r}{\lambda }_{2}p+{\lambda }_{3}p=\frac{1}{2}\\ {\lambda }_2{p}^2+{\lambda }_3{q}^2=\frac{1}{3}\\ {\lambda }_{3}pqs=\frac{1}{6}\end{array}$$

故可选取
$$\begin{array}{rl}{y}_{n+1}=& y_n+\frac{h}{6}(K_1+4K_2+K_3)\\ K_1=& f(x_n,y_n)\\ K_2=& f(x_n+\frac{h}{2},y_n+\frac{h}{2}{K}_1)\\ K_3=& f(x_n+h,y_n-h{K}_1+2h{K}_2)\end{array}$$

四阶Runge-Kutta亦然，其比较常用的形式为

$$\begin{array}{rl}{y}_{n+1}=& y_n+\frac{h}{6}(K_1+2K_2+2K_3+K_4)\\ K_1=& f(x_n,y_n)\\ K_2=& f(x_n+\frac{h}{2},y_n+\frac{h}{2}{K}_1)\\ K_3=& f(x_n+\frac{h}{2},y_n+\frac{h}{2}{K}_2)\\ K_3=& f(x_n+h,y_n+h{K}_2)\end{array}$$

# Runge-Kutta法
# f为dy/dx=f(x,y), x为输入区间[x1,x2]，n为步长
# deg为阶数,支持2，3，4阶
# 二阶需要输入参数p,lmd1,lmd2;三阶需要额外输入q,r,s,lmd3
# 四阶需要另输入a,b,c,d,lmd4
function RungeKutta(f,x,y0,n;deg=2;kwargs...)
    h=(x[2]-x[1])/n
    x = [x[1]+i*h for i in 1:n]
    y = zeros(n)
    y[1] = y0

    
    # 初始化参数
    if deg == 2
        p,lmd1,lmd2 = isempty(kwargs) ? [1/2,1/2,1/2] : [
            kwargs[:p],kwargs[:lmd1],kwargs[:lmd2]]
    elseif deg == 3
        p,q,r,s,lmd1,lmd2,lmd3 = isempty(kwargs) ? [
            1/2,1,-1,2,1/6,2/3,1/6] : [kwargs[:p],
            kwargs[:q],kwargs[:r],kwargs[:s],
            kwargs[:lmd1],kwargs[:lmd2],kwargs[:lmd3]]
    elseif deg == 4
        p,q,r,s,a,b,c,d,lmd1,lmd2,lmd3 = isempty(kwargs) ? [
            1/2,1/2,0,0,1,0,1,0,1/6,1/3,1/3,1/6] : [
            kwargs[:p],kwargs[:q],kwargs[:r],kwargs[:s],
            kwargs[:a],kwargs[:b],kwargs[:c],kwargs[:d],
            kwargs[:lmd1],kwargs[:lmd2],kwargs[:lmd3],kwargs[:lmd4]]
    end

    for i in 2:n
        K1 = f(x[i-1],y[i-1])
        K = K1
        if deg>1
            K2 = f(x[i-1]+p*h,y[i-1]+p*h*K1)        #参数p
            K = lmd1*K1+lmd2*K2
        end
        if  deg>2
            K3 = f(x[i-1]+q*h,y[i-1]+q*h*(r*K1+s*K2))#参数q,r,s
            K += lmd3                   #参数lmd3
        end
        if deg>3
            K4 = f(x[i-1]+a*h,y[i-1]+a*h*(b*K1+c*K2+d*K3))
            K += lmd4
        end
        y[i] = y[i-1]+h*K
    end
    return y
end