Attention比较常见的表示是:
从实现角度来看,Q,K,V都是目标特征的线性转换,并不难。然而其中还有一些技术细节比较模糊,为了加深对于Attention的理解,本文总结了一些优质分析和理解,并尝试回答以下几个问题:
(1)Attention中的Q,K,V要怎么理解?
(2)Attention中的softmax要怎么理解?
(3)Attention中的要怎么理解?
1. Q,K,V 的理解
两个向量a和b同向,a·b=|a||b|;a和b垂直,a·b=0;a和b反向,a·b=-|a||b|。所以两个向量的点乘可以表示两个向量的相似度,越相似方向越趋于一致,a点乘b数值越大。从这个角度出发,Q和K的点乘的结果是一个attention score矩阵,矩阵中的数值衡量不同特征之间的相似度,softmax的引入则将上述结果进行归一化,形成一个所有数值为0-1的归一化attention score 矩阵,从而更直观的反映出不同元素之间的关联性差异。最后,将上述attention score矩阵乘上线性变化后的输入V,实现将向量之间的关系作用到向量本身。
2. 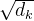 的作用
的作用
softmax的大输入值会导致梯度在反向传播期间消失,为了解决这个问题,可以在softmax内部除以,让梯度回传的时候变得更平稳并且避免梯度消失。
看到这里我们可能会提出以下两个问题:
(1)为啥softmax的大输入值会让梯度在反向传播过程中消失?
(2)为什么除以?
2.1 softmax 的输出结果对于输入数据数量级的敏感性
softmax的函数对于输入的数量级比较敏感,越大的输入越多地支配输出,当目标向量中不同维度的值相差很大时,softmax倾向于将接近1的值分配给最大的输入值,而将0分配给其他所有值。一个比较直观的理解是把向量(1,2,3,1000000)输入到softmax函数中,得到的结果将非常接近(0,0,0,1)。
2.2 梯度在softmax的反向传播受到softmax输出结果的影响
softmax 在形式上是一种向量映射函数,对所有变量的求导结果是一个雅可比矩阵,它由目标函数与所有变量
的一阶偏导数排列构成:
其中,
一个比较关键的特性是,softmax的雅可比矩阵可以由softmax的输出向量所表示,以四维向量为例:
我们可以观察到,对于目标结果向量, 如果第i个特征的值为1,其他特征的值为0,那么该雅可比矩阵将变成0矩阵。也就是说以下四种情况的任何一种都会导致雅可比矩阵变成零矩阵:
,
,
,
值得注意的是,根据我们前面所分析的,对于较大的输入而言,softmax的输出结果正是落在了上述这几种情况之中。带着上述结论,我们可以计算反向传播的梯度了。梯度的计算实际上就是计算Loss函数对于输入变量z的偏导数,这可以通过链式法则计算:
可以看到,当计算目标变量的梯度时,等号右侧的第一项行向量对应着雅可比矩阵中的第j列。在softmax层的梯度反向传播等效于在计算目标梯度的基础上乘以一个softmax函数的雅可比矩阵。因此,对于所有参数的梯度反向传播运算可以表示为:
当输入的值较大时,我们计算的雅可比矩阵已经变成了0矩阵,因此梯度的运算结果就为0,梯度被softmax杀死,这进一步造成了学习速度的减慢甚至完全停止。所以,softmax的大输入值会让梯度在反向传播期间消失。
2.3 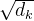
既然是较大输入导致了梯度运算问题,那我们就把较大的输入变小。补救措施是在Q和K的点乘之后除以一个基于特征维度的值
来让点积的结果恢复到之前的分布。为什么是
呢?
假设Q,K中的任意一个元素和
都是服从期望为0,方差为1的独立的随机变量,并且Q和K的特征维度都为
。
为了简化公式,我们让,所以我们能够得到:
为了让点乘之后特征的方差变回到原来的1,我们需要对方差内部的QK进行缩放,此时有:
3. 参考文献
self-attention为什么要除以根号d_k_selfattention为什么要除dk_想念@思恋的博客-CSDN博客
保姆级分析self Attention为何除根号d,看不懂算我的 - 知乎
深度学习attention机制中的Q,K,V分别是从哪来的? - 知乎








 文章详细解释了Attention机制中的Q、K、V的含义,以及softmax在Attention中的作用。Q和K的点乘产生注意力得分,softmax进行归一化,防止大输入值导致的梯度消失问题。除以√d_k是为了保持点乘结果的方差,稳定学习过程。
文章详细解释了Attention机制中的Q、K、V的含义,以及softmax在Attention中的作用。Q和K的点乘产生注意力得分,softmax进行归一化,防止大输入值导致的梯度消失问题。除以√d_k是为了保持点乘结果的方差,稳定学习过程。
















 808
808

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








