EAST（An Efficient and Accurate Scene Text Detector）论文阅读笔记

论文中作者网络（e）与其他网络对比

贡献

1. 只包含两个阶段：全卷积网络（FCN）和非极大值抑制（NMS）。FCN直接产生文本区域，没有冗余和耗时的中间步骤。
2. 可以灵活的生成词级或者行级的预测，它们的几何形状可以是旋转框或者四边形。
3. 采用了Locality-Aware NMS来对生成的几何进行过滤
4. 所提出的算法在精度和速度方面都有所提高

方法

特征提取主干 + 特征合并分支 + 输出层部分

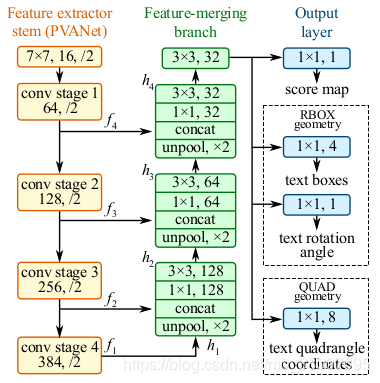
1. Pipeline

该模型是一个全卷积的神经网络，适用于文本检测，输出密集的每个像素预测的单词或文本行。后处理步骤仅包括预测几何形状的阈值和NMS。

其中将图像输入到FCN，并且生成多个像素级文本得分图（Score Map）和几何通道图。预测通道中的一个是得分图，其像素值在[0,1]的范围内。 其余通道表示从每个像素的视图中包围该单词的几何。 分数代表在相同位置预测的几何形状的置信度。

两种几何形状（旋转框RBOX和四边形QUAD），分别设计了不同的损失函数。使用阈值过滤掉一些几何，然后NMS，得到最终输出。

2.Network Design（网络设计）

特征融合（结合不同级别的网络特征）。为了降低计算成本没有采用HyperNet，而是采用了U形网络的思想。

特征提取主干 + 特征合并分支 + 输出层部分

• 特征能提取主干：用于提取特征，采用 PVANet（文末的代码中使用的是ResNet_v1_50）

• 特征合并分支：

  • 在每个合并阶段，使用最后一个阶段的feature map 进行uppooling（上采样将原图像放大2倍）

  • 然后与前一层 feature map 连接 concatenate

  • 接着使用1×1卷积核减少通道数量并减少计算（卷积核的个数128，64，32）

  • 然后使用3×3卷积核产生该合并阶段的输出（卷积核的个数128，64，32）

    在最后一个合并阶段，使用只使用3x3的卷积核产生合并阶段最终的feature map，并给输出层。

• 输出层，有若干1×1卷积操作，将32通道的特征图投影到 1通道的得分图$F_s$ 和 多通道几何图$F_g$中。 几何输出可以是RBOX或QUAD。（文末的代码中只实现了RBOX）

  • RBOX 几何形状由4个通道的轴对齐边界框（AABB）R和1个通道旋转角θ表示。其中4个通道分别表示从像素位置到矩形的顶部，右侧，底部，左部的4个距离。
  • QUAD 使用8个数字来表示从四边形的四个角顶点 { p i ∣ i ∈ { 1 , 4 , 3 , 4 } } \{p_i|i∈\{1,4,3,4\}\} {pi​∣i∈{1,4,3,4}}到像素位置的距离。 每一个距离包含两个数字$(\Delta x_i,\Delta y_i)$，因此几何输出包含8个通道。

3.Label Generation（标签生成）

标签生成流程图

（a）文本四边形（黄色虚线）和压缩四边形（绿色实线）
（b）文本分数图（text score map）
（c）RBOX几何图生成
（d）每个像素到矩形边界的4个通道距离
（e）旋转角度

1. 分数图（Score Map）的生成

   • 分数图上四边形的正面积设计为原始面积的缩小版

   • 对于四边形 Q = { p i ∣ i ∈ 1 , 2 , 3 , 4 } Q = \{p_i|i∈{1,2,3,4}\} Q={pi​∣i∈1,2,3,4}，其中 p i = { x i , y i } p_i = \{x_i, y_i\} pi​={xi​,yi​}是四边形上的顶点，以顺时针顺序排列。 为了缩小Q，我们首先计算每个顶点$p_i$的参考长度$r_i$
     $$r_i=min(D(p_i,p_{(imod4)+1}),D(p_i,p_{((i+2)mod4)+1}))$$
     此处 $D(p_i,p_j)$是 $p_i$ 和 $p_j$ 的 L2 距离

     我们首先缩小四边形的两个较长边，然后缩短两个较短边。对于每对两个相对的边，我们通过比较它们的长度的平均值来确定“更长”的对。 对于每个边$<p_i,p_{(imod4)+1}>$，我们通过将其两个端点沿边缘向内移动$0.3r_i$和$0.3r_{(imod4)+1}$来缩小它。

2. 几何图（Geometry Map）的生成

   对于那些文本区域以QUAD样式注释的数据集（例如，ICDAR 2015），首先生成一个旋转矩形，用最小的面积覆盖区域。然后对于每个具有正分数的像素，我们计算它到文本框的4个边界的距离，并将它们放到RBOX ground truth 的 4 个通道中。 对于QUAD ground truth，8通道几何图中具有正分数的每个像素的值是其从四边形的4个顶点的坐标偏移。

4. Loss Functions（损失函数）

$$L=L_s+{\lambda }_g{L}_g$$

$L_s$代表分数损失，$L_g$代表几何的损失，${\lambda }_g$代表两个损失的重要性​，在论文中，设置为1

1. Loss for Score Map ($L_s$)

​ 类平衡交叉熵（class-balanced cross-entropy）:用于解决类别不平衡训练，避免通过 平衡采样和硬负挖掘 解决目标物体的不平衡分布，简化训练过程

$$L_s=balanced-xent(\hat{Y},Y^{\ast })=-\beta Y^{\ast }log\hat{Y}-(1-\beta )(1-Y^{\ast })log(1-\hat{Y})$$
这里 $\hat{Y}$ 是score map 的预测值，$Y^{\ast }$是Ground Truth。参数 $\beta$ 是正样本和负样本的平衡因子：
$$\beta =1-\frac{{\sum }_{y^{\ast }\in Y^{\ast }}{y}^{\ast }}{|Y^{\ast }|}$$

在文末的代码中实现这部分损失使用的是 dice classification loss ，而不是文中的class-balanced cross-entropy，关于这两个损失哪个好，可以阅读文章 Generalised Dice overlap as a deep learning loss function for highly unbalanced segmentations，或者自己尝试一下。

2. Loss for Geometries ($L_g$)

​ 文本在自然场景中的尺寸变化极大。直接使用L1或者L2损失去回归文本区域将导致损失偏差朝更大更长．因此论文中采用IoU损失在 RBOX 回归的 AABB 部分，尺度归一化的 smoothed-L1 损失在 QUAD 回归，来保证几何形状的回归损失是尺度不变的

• RBOX

  交并比损失
  $$L_{AABB}=-logIoU(\hat{R},R^{\ast })=-log\frac{|\hat{R}\cap R^{\ast }|}{|\hat{R}\cup R^{\ast }|}$$
  $\hat{R}$ 代表AABB四边形的预测，$R^{\ast }$是对应的Ground Truth，$|\hat{R}\cap R^{\ast }|$的宽和高是：
  $$\begin{gathered} w_i=min(\widehat{d_2},d_2^{\ast })+min(\widehat{d_4},d_4^{\ast }) \\ {h}_i=min(\widehat{d_1},d_1^{\ast })+min(\widehat{d_3},d_3^{\ast }) \end{gathered}$$
  $d_1$, $d_2$, $d_3$, $d_4$代表从一个像素到它对应矩形的顶部，右边，底部，左边的距离，相交的面积为：
  $$|\hat{R}\cup R^{\ast }|=|\hat{R}|+|R^{\ast }|-|\hat{R}\cap R^{\ast }|$$
  接下来，旋转角的损失计算：
  $$L_{\theta }(\hat{\theta },{\theta }^{\ast })=1-cos(\hat{\theta }-{\theta }^{\ast })$$
  $\hat{\theta }$是预测的旋转角，${\theta }^{\ast }$是Ground Truth。最后，总体损失为AABB损失和旋转角损失的加权和：
  $$L_g=L_{AABB}+{\lambda }_{\theta }{L}_{\theta }$$
  论文中${\lambda }_{\theta }$设置为10。

• QUAD

  添加归一化的 Smoothed-L1
  C Q = { x 1 , y 1 , x 2 , y 2 , . . . , x 4 , y 4 } C_Q = \{x_1, y_1, x_2, y_2, ..., x_4, y_4\} CQ​={x1​,y1​,x2​,y2​,...,x4​,y4​}
  损失值：
  $$L_g=L_{QUAD}(\hat{Q},Q^{\ast })=\underset{\tilde{Q}\in P_{Q^{\ast }}}{\min }\sum _{c_i\in C_Q\widetilde{c_i}\in C_{\tilde{Q}}}\frac{smoothe{d}_{L1}(c_i-\widetilde{c_i})}{8\times N_{Q^{\ast }}}$$
  其中归一化项$N_{Q^{\ast }}$是四边形的短边长度，由下式给出
  $$N_{Q^{\ast }}=\underset{i=1}{\overset{4}{\min }}D(p_i,p_{(imod4)+1})$$
  $P_Q$是具有不同顶点排序的$Q^{\ast }$的所有等效四边形的集合。 由于公共训练数据集中的四边形标注不一致，因此需要这种排序排列。

5. Locality-Aware NMS（局部感知NMS）

由于本文产生的几何体数量加大，使用普通的NMS时间复杂度太高（$O(n^2)$），针对这个，提出了基于行合并几何体的方法（加权平均）。

假设来自邻近像素的几何形状倾向于高度相关，就逐行合并几何，并且在同一行中合并几何形状时，我们将迭代地合并相邻两个四边形。 这种改进的技术在最佳场景（只有一个文本行出现在图像中的情况。 在这种情况下，如果网络足够强大，所有几何形状将高度重叠）中以$O(n)$运行。 即使最坏的情况也与普通NMS情况相同，只要假设成立，算法就会在实践中运行得足够快。

首先按照 $y$ 轴坐标对四边形进行排序，进行逐行遍历，相邻的两个四边形 $p$ 和 $q$ 达到设定的阈值便进行合并，否则不进行合并。 $S$ 中存储的是合并之后的四边形。合并之后再进行标准的NMS。

合并： 在 $WEGHTMERGE(g,p)$ 中，合并四边形的坐标通过两个给定四边形的分数进行加权平均。若 $a=WEGHTMERGE(g,p)$ ，则 $a_i=V(g)g_i+V(p)p_i$ 且 $V(a)=V(g)+V(p)$ ，$a_i$ 是 $a$ 在 $i$ 处的坐标，$V(a)$ 是四边形 $a$ 的得分。

论文中给出的检测效果图：

总结

EAST由于感受野不够大，所以对较长文本行检测效果不是太好，比较适合短文本行检测。

CTPN由于LSTM的存在，对长文字的检测效果比EAST好，但是对于倾斜的文本行检测效果不太好。

参考文章及代码

EAST论文：https://arxiv.org/abs/1704.03155

EAST代码：https://github.com/argman/EAST