[超简单] 临床决策曲线 Decision curve analysis (DCA) 快速入门概要

欣欣影像科研速递

已于 2024-11-12 16:53:45 修改

阅读量1.9k

点赞数

文章标签：机器学习 python 算法生存分析临床决策曲线医学

于 2024-10-17 10:18:44 首次发布

原文链接：https://cran.r-project.org/web/packages/dcurves/vignettes/dca.html

版权

介绍

Decision curve analysis (DCA) 是一种评估和比较预测模型的方法，它考虑了临床后果，只需要在模型测试的数据集上进行，并且可以应用于连续或二分类结果的模型。

DCA 的核心思想是比较不同预测模型的净获益，即在不同阈值下，模型预测与实际发生事件之间的一致性所带来的获益与不一致性所带来的损失之间的差异。

在进行 DCA 时，通常会比较两种默认策略：

假设所有患者都是阳性，因此对所有人进行治疗（“治疗所有”策略）。
假设所有患者都是阴性，因此不对任何人进行治疗（“不治疗所有”策略）。

“治疗”在这里被理解为最广泛的含义，不仅包括药物、放疗或手术，还包括建议、进一步的诊断程序或更密集的监测。

进行 DCA 的步骤通常包括：

确定模型预测的概率阈值。
计算在不同阈值下，模型预测为阳性的患者比例。
计算在不同阈值下，模型预测与实际发生事件之间的一致性比例。
计算净获益，即一致性比例与不一致性比例之间的差异。
绘制决策曲线，横轴为模型预测的概率阈值，纵轴为净获益。
比较不同模型的决策曲线，曲线越靠上，表示模型的预测能力越强。

对于二分类结果，DCA 的过程相对简单，因为结果只有两种可能：阳性或阴性。而对于时间至事件（time-to-event）结果，可能需要更复杂的统计方法来处理生存时间数据。

二分类结果Binary Outcomes

单变量临床决策曲线分析 Univariate Decision Curve Analysis

我们将使用随包附带的示例数据集 df_binary。该数据集包含了750名最近发现他们携带一种基因突变的患者的信息，这种基因突变使他们有更高的患癌症风险。每位患者都进行了活检，我们知道他们的癌症状况。已知年龄较大的患者如果有癌症家族史，患癌症的概率更高。一位临床化学家最近发现了一个标记物，她认为这个标记物可以区分患有和没有癌症的患者。我们希望评估这个新标记物是否真的能够识别患有和没有癌症的患者。如果这个标记物确实预测得很好，许多患者将不需要经历痛苦的活检。

首先，我们想要确认癌症家族史确实与活检结果相关联。

mod <- glm(cancer ~ famhistory, df_binary, family = binomial)
tbl <- tbl_regression(mod, exponentiate = TRUE)
tbl

通过进行以癌症为结果变量的逻辑回归分析，我们可以看到家族史与活检结果相关，比值比（OR）为1.80（95%置信区间1.07, 2.96；p=0.022）。这意味着有癌症家族史的患者活检结果呈阳性的可能性是没有家族史患者的1.80倍。这个p值小于0.05，表明这种关联在统计上是显著的。

dca(cancer ~ famhistory, df_binary) %>%
  plot(smooth = TRUE)

首先，请注意这里展示的许多阈值概率并不是我们感兴趣的。例如，不太可能有患者要求他们至少有50%的癌症风险才愿意接受活检。让我们再次进行DCA，这次将输出限制在一个更符合临床实际的阈值概率范围内，即0%到35%之间。

dca(cancer ~ famhistory, df_binary, thresholds = seq(0, 0.35, by = 0.01)) %>%
  plot(smooth = TRUE)

现在图表显示了一个更合理的阈值概率范围，让我们来评估单独使用家族史的临床效用。我们可以看到，尽管家族史与活检结果显著相关，但它只在接近13%到20%的一小部分阈值概率范围内增加价值。如果你的个人阈值概率是15%（即如果癌症的概率大于15%，你将接受活检），那么单独使用家族史在决定是否进行活检时可能是有益的。然而，如果你的阈值概率低于13%或高于20%，那么家族史并没有比“全部活检”或“不活检”的方案带来更多的好处。

多变量临床决策曲线分析 Multivariable Decision Curve Analysis

新模型评估

我们想要检验一个包含家族史、年龄和标记物的统计模型的价值。首先，我们将构建一个包含所有三个变量的逻辑回归模型，其次我们将保存基于该模型预测的患癌症的概率。请注意，在我们示例数据集中，这个变量实际上已经存在，因此不需要再次创建预测概率。

glm(cancer ~ marker + age + famhistory, df_binary, family = binomial) %>%
  broom::augment(newdata = df_binary, type.predict = "response")
#> # A tibble: 750 × 9
#>    patientid cancer  dead risk_group     age famhistory marker cancerpredmarker
#>        <dbl> <lgl>  <dbl> <chr>        <dbl>      <dbl>  <dbl>            <dbl>
#>  1         1 FALSE      0 low           64.0          0 0.776           0.0372 
#>  2         2 FALSE      0 high          78.5          0 0.267           0.579  
#>  3         3 FALSE      0 low           64.1          0 0.170           0.0216 
#>  4         4 FALSE      0 low           58.5          0 0.0240          0.00391
#>  5         5 FALSE      0 low           64.0          0 0.0709          0.0188 
#>  6         6 FALSE      0 intermediate  65.7          0 0.428           0.0426 
#>  7         7 FALSE      1 intermediate  71.9          0 0.942           0.296  
#>  8         8 TRUE       0 intermediate  66.6          0 2.91            0.387  
#>  9         9 FALSE      0 low           64.3          0 0.715           0.0373 
#> 10        10 FALSE      0 intermediate  65.7          0 0.129           0.0320 
#> # ℹ 740 more rows
#> # ℹ 1 more variable: .fitted <dbl>

我们现在想要比较不同的癌症检测方法：对所有人进行活检、不对任何人进行活检、基于家族史进行活检，或者基于包括标记物、年龄和癌症家族史的多变量统计模型进行活检。

dca(cancer ~ famhistory + cancerpredmarker, 
    data = df_binary, 
    thresholds = seq(0, 0.35, by = 0.01)) %>%
  plot(smooth = TRUE)

决策曲线分析的关键方面是观察哪种策略能带来最大的净获益（即“最高”的线），在这个例子中，这将对应于包括年龄、癌症家族史和标记物的模型。很明显，在合理的阈值概率范围内，基于这个多变量模型做决策是不会错的：它是优越的，与任何其他策略不同，它永远不会更糟。

有几个要点值得注意。首先，看看绿色线，即“治疗所有”的净获益，也就是对所有人进行活检。这条线在y轴上的截距是患病率。想象一下，如果一个人的风险阈值是14%，他询问在“活检所有人”策略下的风险，他会得知他的风险是患病率（14%）。当患者的风险阈值与预测风险相同时，活检和不活检的净获益是相同的。

其次，二元变量（癌症家族史，青绿色线）的决策曲线在1 - 阴性预测值处与“活检所有男性”线相交，这很容易解释：阴性预测值是87%，所以没有癌症家族史的患者患病概率是13%；阈值概率低于这个值的患者——例如，即使风险是10%也会选择活检的患者——因此即使他/她没有癌症家族史，也应该进行活检。

二元变量的决策曲线在阳性预测值处等同于不对任何人进行活检。这是因为对于二元变量，具有该特征的患者被赋予了阳性预测值的风险。

已发布模型评估

假设 Brown 等人发表了一个关于我们的癌症活检数据集的模型。作者报告了一个统计模型，其中癌症家族史阳性的系数为 0.75；每增加一岁年龄的系数为 0.26，截距为 -17.5。为了在我们的数据集上测试这个公式：

df_binary_updated <-
  df_binary %>%
  mutate(
    # Use the coefficients from the Brown model
    logodds_Brown = 0.75 * (famhistory) + 0.26 * (age) - 17.5,
    # Convert to predicted probability
    phat_Brown = exp(logodds_Brown) / (1 + exp(logodds_Brown))
  )

# Run the decision curve
dca(cancer ~ phat_Brown, 
    data = df_binary_updated, 
    thresholds = seq(0, 0.35, by = 0.01),
    label = list(phat_Brown = "Brown Model")) %>%
  plot(smooth = TRUE)

这条决策曲线表明，尽管该模型可能对风险厌恶型患者有用，但实际上对具有更适度阈值概率的患者是有害的。因此，Brown 等人的模型不应在临床实践中使用。这种模型有害的效果，是由于校准不当造成的，即当给患者的风险过高或过低时。请注意，当模型在相同的数据集上创建和测试时，校准不当很少发生，例如在我们创建了包含家族史和标记物的模型的例子中。

联合或条件测试

在医学中，许多决策都是基于联合或条件测试结果的。一个经典的例子是，根据测试结果将患者归类为高风险、低风险或中等风险。高风险患者会立即被推荐进行治疗（在我们的例子中是进行活检）；低风险患者会被安抚并告知无需进一步行动；中等风险患者会被送去进行额外的测试，随后根据测试结果做出相应的治疗决策。

想象一下，对于我们的例子，之前有一个测试将我们的患者归类为高、低和中等癌症风险，我们想要结合我们的标记物。有五种临床选项：

对所有人进行活检
不对任何人进行活检
对被确定为高癌症风险的患者进行活检；不使用标记物
对所有人测量标记物，然后对那些被确定为高癌症风险或根据标记物确定的癌症概率超过一定水平的人进行活检（即联合方法）
对所有高风险患者进行活检；对中等风险患者测量标记物，并根据标记物确定的癌症概率超过一定水平的人进行活检（即条件方法）

决策曲线分析可以结合联合或条件测试。所需的只是从数据集中计算适当的变量；然后像平常一样计算决策曲线。首先，我们会创建代表我们联合和条件方法的变量。对于我们的例子，让我们使用0.15作为对那些进行了标记物测量并且应该进行活检的患者的概率截止水平。

df_binary_updated <-
  df_binary_updated %>%
  mutate(
    # Create a variable for the strategy of treating only high risk patients
    # This will be 1 for treat and 0 for don't treat
    high_risk = ifelse(risk_group == "high", 1, 0),
    # Treat based on Joint Approach
    joint = ifelse(risk_group == "high" | cancerpredmarker > 0.15, 1, 0),
    # Treat based on Conditional Approach
    conditional = ifelse(risk_group == "high" | 
                           (risk_group == "intermediate" & cancerpredmarker > 0.15), 1, 0)
  )

现在我们已经计算出了变量，我们可以运行决策曲线分析。

dca(cancer ~ high_risk + joint + conditional, 
    data = df_binary_updated, 
    thresholds = seq(0, 0.35, by = 0.01)) %>%
  plot(smooth = TRUE)

这似乎表明，在5%到24%的阈值概率范围内，联合测试是更好的选择，因为它在这个范围内具有最高的净获益。在低于5%的情况下，对所有人进行治疗的临床选择将优于其他任何选择，尽管治疗阈值很少会这么低。从28%到35%，条件测试会是稍微更好的选择，而在这两个范围之间，联合测试和条件测试是可比的。联合测试的明显缺点是，需要为每个人测量标记物，这样的测试可能既昂贵又耗时。

在模型评估中纳入危害（Harms）

为了将测试和测量标记物的危害纳入考量，我们咨询了一位临床医生，他告诉我们，即使标记物完全准确，也很少有临床医生会进行超过30次测试来预测一次癌症诊断。这可能是因为测试成本高昂，或者需要某种侵入性程序来获取样本。测量标记物的“危害”是30的倒数，即0.0333。

为了构建每种策略的决策曲线，我们现在需要纳入危害。我们必须特别为条件测试计算危害，因为只有中等风险的患者才会被测量标记物。然后将危害纳入我们的决策曲线。对于条件测试纳入危害的策略是通过将被扫描的比例乘以扫描的危害来实现的。

# the harm of measuring the marker is stored in a scalar
harm_marker <- 0.0333

# in the conditional test, only patients at intermediate risk have their marker measured
intermediate_risk <- df_binary_updated$risk_group == "intermediate"

# harm of the conditional approach is proportion of patients who have the marker measured multiplied by the harm
harm_conditional <- mean(intermediate_risk) * harm_marker

# Run the decision curve 
dca_with_harms <-
  dca(cancer ~ high_risk + joint + conditional, 
    data = df_binary_updated, 
    harm = list(joint = harm_marker, conditional = harm_conditional),
    thresholds = seq(0, 0.35, by = 0.01))
plot(dca_with_harms, smooth = TRUE)

在这里，条件测试显然是最佳选择（在8%的治疗阈值以上），实际上，一旦考虑到测量标记物的危害，对每个人进行标记物测量显然是不值得的：仅仅治疗高风险患者的净获益通常高于联合测试的净获益。

输出净获益值Saving out Net Benefit Values

对于通过决策曲线分析评估的任何模型，如果我们还想在表格中显示净获益，我们可以将它们输出。对于特定范围的值，我们只需要指定开始的阈值、结束的阈值以及我们想要使用的增量。

假设我们想要查看仅使用标记物来预测患者是否患有癌症的净获益，与在5%、10%、15%……35%的阈值下对所有患者进行活检的净获益进行比较。对于模型本身，我们实际上需要首先指明标记物变量——与之前任何模型的变量不同——不是一个概率。根据我们的阈值，我们希望从0.05开始，以0.05的增量，到0.35结束。

dca_with_harms %>%
  as_tibble() %>%
  filter(threshold %in% seq(0.05, 0.35, by = 0.05)) %>%
  select(variable, threshold, net_benefit) %>%
  pivot_wider(id_cols = threshold, 
              names_from = variable,
              values_from = net_benefit)
#> # A tibble: 6 × 6
#>   threshold     all  none high_risk    joint conditional
#>       <dbl>   <dbl> <dbl>     <dbl>    <dbl>       <dbl>
#> 1      0.05  0.0947     0    0.0168  0.0671      0.0740 
#> 2      0.1   0.0444     0    0.0161  0.0571      0.0662 
#> 3      0.2  -0.075      0    0.0147  0.0334      0.0475 
#> 4      0.25 -0.147      0    0.0138  0.0191      0.0362 
#> 5      0.3  -0.229      0    0.0128  0.00289     0.0234 
#> 6      0.35 -0.323      0    0.0116 -0.0159      0.00861

净获益具有直接的临床解释。在20%的阈值概率下，0.03的值可以这样解释：“与不进行任何活检相比，基于标记物进行活检相当于一种策略，该策略在不进行任何不必要的活检的情况下，每百名患者中发现了3例癌症。”

避免干预 Interventions Avoided

作为评估标记物实用性的一部分，我们感兴趣的是，使用这个标记物来识别患有和没有癌症的患者是否有助于减少不必要的活检。这个值是保存输出表格中的“避免干预”列。要图形化地查看它，我们只需要在我们的命令中指定它。

dca(cancer ~ marker, 
    data = df_binary, 
    as_probability = "marker") %>%
  net_intervention_avoided() %>%
  plot(smooth = TRUE)

在15%的概率阈值下，干预措施的净减少大约是0.33。换句话说，在这一概率阈值下，基于标记物对患者进行活检相当于一种策略，该策略在不漏诊任何癌症的情况下，将活检率降低了33%。

生存分析结果 Survival Outcomes

在这种情况下，患者已经测量了一种标记物，并且对他们进行了随访，以确定他们是否最终被诊断出癌症。我们希望使用年龄、家族史和标记物来构建一个模型，并评估这个模型在1.5年内预测癌症的效果如何。在本教程的这一部分中，我们将使用以下变量从示例数据集中进行分析：

年龄（Age）：通常，年龄是预测多种健康问题风险的重要因素，包括癌症。
家族史（Family History）：有癌症家族史的人可能面临更高的癌症风险。
标记物（Marker）：这是一种生物标志物，可能与癌症风险相关。

library(survival)
df_surv %>% head()
#> # A tibble: 6 × 9
#>   patientid cancer ttcancer risk_group    age famhistory marker cancerpredmarker
#>       <dbl> <lgl>     <dbl> <chr>       <dbl>      <dbl>  <dbl>            <dbl>
#> 1         1 FALSE    3.01   low          64.0          0 0.776           0.0372 
#> 2         2 FALSE    0.249  high         78.5          0 0.267           0.579  
#> 3         3 FALSE    1.59   low          64.1          0 0.170           0.0216 
#> 4         4 FALSE    3.46   low          58.5          0 0.0240          0.00391
#> 5         5 FALSE    3.33   low          64.0          0 0.0709          0.0188 
#> 6         6 FALSE    0.0488 intermedia…  65.7          0 0.428           0.0426 
#> # ℹ 1 more variable: cancer_cr <fct>

基本数据

任何时间点的生存概率都可以从任何类型的生存模型中得出；这里我们使用 Cox，因为这是统计实践中最常见的模型。 Cox 模型的生存概率公式由下式给出

在Cox模型中，X 是协变量矩阵，β 是包含Cox模型参数估计值的向量，S0(t) 是到时间 t 的基线生存概率。为了在我们的代码中获得这些值，我们将使用年龄、家族史和标记物作为预测因子运行Cox模型，保存基线生存函数到一个新的变量中，并为每个受试者获得模型的线性预测。

然后我们获得我们感兴趣的时间点的基线生存概率。如果没有患者在确切的感兴趣时间被观察到，我们可以使用基线生存概率到最接近但不在时间点之后的观察时间。然后我们可以计算在指定时间点的失败概率。对于我们的例子，我们将使用1.5年作为一个时间点。

# build Cox model
cox_model <- coxph(Surv(ttcancer, cancer) ~ age + famhistory + marker, data = df_surv)

# show summary of model results
tbl_regression(cox_model, exponentiate = TRUE)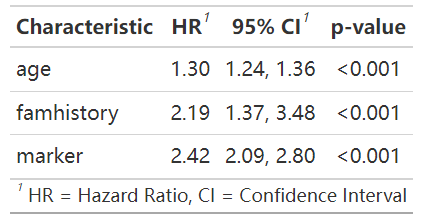

# add model prediction to our data frame
df_surv_updated <-
  broom::augment(
    cox_model, 
    newdata = df_surv %>% mutate(ttcancer =  1.5),
    type.predict = "expected"
  ) %>%
    mutate(
      pr_failure18 = 1 - exp(-.fitted)
    ) %>%
    select(-.fitted, -.se.fit)

在计算出失败概率之后，运行决策曲线分析的代码就很简单了。我们所要做的就是指定我们感兴趣的时间点。对于我们的例子，让我们不仅将阈值从0%设置到50%，还要添加平滑处理。平滑曲线的结果应该总是与未平滑的曲线进行比较，以确保准确性。

dca(Surv(ttcancer, cancer) ~ pr_failure18, 
    data = df_surv_updated,
    time = 1.5,
    thresholds = 1:50 / 100) %>%
  plot(smooth = TRUE)

这表明，使用该模型为临床决策提供信息将为任何与阈值概率高于 2% 左右相关的决策带来更好的结果。

竞争风险Competing Risks

竞争风险终点的处理方式与生存终点类似。结果必须被定义为一个因素，最低级别称为“审查”，其他级别定义感兴趣的事件。 dca() 函数会将列出的第一个结果视为感兴趣的结果。

dca(Surv(ttcancer, cancer_cr) ~ pr_failure18, 
    data = df_surv_updated,
    time = 1.5,
    thresholds = 1:50 / 100) %>%
  plot(smooth = TRUE)

病例对照数据Case-Control Data

病例对照数据的处理方式类似于二分类数据，不同之处在于必须指定结果的发生率，因为无法从数据中估计出该发生率。,

dca(casecontrol ~ cancerpredmarker, 
    data = df_case_control,
    prevalence = 0.15) %>%
  plot(smooth = TRUE)
#> Assuming '1' is [Event] and '0' is [non-Event]