概率论复习笔记(二)随机变量及其分布
基本概念
随机变量及其分布函数
随机变量 : 设随机试验 E E E的样本空间为 Ω \Omega Ω, 如果对于 Ω \Omega Ω内的每一个样本点 e e e都有一个实数x 与之对应, 则称 X X X为随机变量, 记为 X = X ( e ) . X= X(e). X=X(e).
简言之, 随机变量就是定义在样本空间 Ω \Omega Ω上的样本点 e 的实值单值函数 X ( e ) . X(e). X(e).我们一般用大写字母如 X , Y , Z , … X,Y,Z,\dots X,Y,Z,…表示随机变量 。
随机变量的分类 :
随
机
变
量
{
离
散
型
非
离
散
型
{
连
续
型
其
他
随机变量 \begin{cases} 离散型 \\ 非离散型 \begin{cases} 连续型 \\ 其他 \end{cases} \end{cases}
随机变量⎩⎪⎨⎪⎧离散型非离散型{连续型其他
不要误以为 , 一个随机变量如果不是离散型就是连续型的.实际上还存在非离散非连续型的 。
随机变量的取值是有概率规律的, 这种概率规律叫做随机变量的概率分布.在概率分布的描述上,离散型随机变量和连续型随机变量所采用的方法是不同的.前者主要采用列举法, 后者主要采用积分法.
分布函数
设
X
X
X 是一个随机变量
,
x
,x
,x是任意实数, 函数
F
(
x
)
=
P
{
X
≤
x
}
,
−
∞
<
x
<
∞
F(x)=P\{X\leq x\},-\infty<x<\infty
F(x)=P{X≤x},−∞<x<∞
称为 X X X的分布函数.
分布函数的性质
-
单调性: F ( x ) F(x) F(x)是一个单调不减的函数, 即当 x 1 < x 2 x_1<x_2 x1<x2时 , F ( x 1 ) ≤ F ( x 2 ) ; ,F(x_1)\leq F(x_2); ,F(x1)≤F(x2);
-
有界性 :
0 ≤ F ( x 1 ) ≤ 1 , 且 F ( + ∞ ) = lim x → + ∞ F ( x ) = 1 ; F ( − ∞ ) = lim x → − ∞ F ( x ) = 0 ; 0\leq F(x_1)\leq 1,且\\ F(+\infty)=\lim_{x\to+\infty}F(x)=1;\\ F(-\infty)=\lim_{x\to-\infty}F(x)=0; 0≤F(x1)≤1,且F(+∞)=x→+∞limF(x)=1;F(−∞)=x→−∞limF(x)=0; -
连续性: F ( x + 0 ) = F ( x ) , F(x+0)=F(x), F(x+0)=F(x),即 F ( x ) F(x) F(x)是右连续函数.
用分布函数表示概率:
P { X = a } = P { X ≤ a } − P { X < a } = F ( a ) − F ( a − 0 ) P { X > a } = 1 − P { X ≤ a } = 1 − F ( a ) P { a < X ≤ b } = P { X ≤ b } − P { X ≤ a } = F ( b ) − F ( a ) P { a < X < b } = P { X < b } − P { X ≤ a } = F ( b − 0 ) − F ( a ) P { a ≤ X ≤ b } = P { X ≤ b } − P { X < a } = F ( b ) − F ( a − 0 ) P { a ≤ X < b } = P { X < b } − P { X < a } = F ( b − 0 ) − F ( a − 0 ) P\{X=a\}=P\{X\leq a\}-P\{X<a\}=F(a)-F(a-0)\\ P\{X>a\}=1-P\{X\leq a\}=1-F(a)\\ P\{a<X\leq b\}=P\{X\leq b\}-P\{X\leq a\}=F(b)-F(a)\\ P\{a<X<b\}=P\{X<b\}-P\{X\leq a\}=F(b-0)-F(a)\\ P\{a\leq X\leq b\}=P\{X\leq b\}-P\{X<a\}=F(b)-F(a-0)\\ P\{a\leq X<b\}=P\{X<b\}-P\{X<a\}=F(b-0)-F(a-0)\\ P{X=a}=P{X≤a}−P{X<a}=F(a)−F(a−0)P{X>a}=1−P{X≤a}=1−F(a)P{a<X≤b}=P{X≤b}−P{X≤a}=F(b)−F(a)P{a<X<b}=P{X<b}−P{X≤a}=F(b−0)−F(a)P{a≤X≤b}=P{X≤b}−P{X<a}=F(b)−F(a−0)P{a≤X<b}=P{X<b}−P{X<a}=F(b−0)−F(a−0)
离散型随机变量及其概率分布
离散型随机变量
若随机变量 X X X的全部可能取值是有限个或可列个, 则称 X X X为离散型随机变量.
分布律
离散型随机变量 X X X所有可能取值为 x k ( k = 1 , 2 , ⋯ ) , x_k(k=1,2,\cdots), xk(k=1,2,⋯), 事件 { X = x k } \{X=x_k\} {X=xk}的概率为 P { X = x k } = p k ( k = 1 , 2 , ⋯ ) , P\{X=x_k\}=p_k(k=1,2,\cdots), P{X=xk}=pk(k=1,2,⋯),这里有 0 ≤ p k ≤ 1 , 0\leq p_k\leq 1, 0≤pk≤1,并且 ∑ k p k = 1 \sum_kp_k=1 k∑pk=1则 称 P { X = x k } = p k ( k = 1 , 2 , ⋯ ) P\{X=x_k\}=p_k(k=1,2,\cdots) P{X=xk}=pk(k=1,2,⋯)为 X X X的分布律或分布列。
分布律也可以写成表格形式:
| X X X | x 1 x_1 x1 | x 2 x_2 x2 | ⋯ \cdots ⋯ | x k x_k xk | ⋯ \cdots ⋯ |
|---|---|---|---|---|---|
| P P P | p 1 p_1 p1 | p 2 p_2 p2 | ⋯ \cdots ⋯ | p k p_k pk | ⋯ \cdots ⋯ |
性质
离散型随机变量 x的分布律的性质:
- P { X = x k } = p k ≥ 0 ( k = 1 , 2 , ⋯ ) P\{X=x_k\}=p_k\geq0(k=1,2,\cdots) P{X=xk}=pk≥0(k=1,2,⋯)
- ∑ k P { X = x k } = ∑ k p k = 1 \sum_kP\{X=x_k\}=\sum_kp_k=1 k∑P{X=xk}=k∑pk=1
离散型随机变量 X X X的分布律与分布函数和事件概率的关系
- 如果已知 X X X的分布律为 P { X = x k } = p k ( k = 1 , 2 , ⋯ ) , P\{X=x_k\}=p_k(k=1,2,\cdots), P{X=xk}=pk(k=1,2,⋯),则 X X X的分布函数
F ( x ) = P { X ≤ x } = ∑ x k ≤ x p k ; F(x)=P\{X\leq x\}=\sum_{x_k\leq x}p_k; F(x)=P{X≤x}=xk≤x∑pk;
而事件的概率为
P
{
a
<
X
≤
b
}
=
∑
a
<
x
k
≤
b
p
k
.
P\{a<X\leq b\}=\sum_{a<x_k\leq b}p_k.
P{a<X≤b}=a<xk≤b∑pk.
- 如果已知
X
X
X的分布函数
F
(
x
)
,
F(x),
F(x),则
X
X
X的分布律为
P { X = x k } = F ( x k ) — F ( x k — 0 ) , k = 1 , 2 , ⋯ , P\{X=x_k \}=F( x_ k ) — F ( x_ k — 0),k=1,2,\cdots, P{X=xk}=F(xk)—F(xk—0),k=1,2,⋯,
F ( x ) F(x) F(x) 的值是 X = x X=x X=x点的左边(含 x x x点)全部所有点概率值的累加和.
F ( x ) F(x) F(x)的图形是右升的台阶形, 每个台阶处的跃度等于 X X X取该值的概率.基于这点 , 由 X X X的分布函数的图形可以求出 X X X的分布律
几个重要的离散型随机变量
(0—1) 分布
设随机变量 X只可能取 0 与1 两个值, 它的分布律是 P { X = k } = p k ( 1 − p ) 1 − k , k = 0 , 1 , 0 < p < 1 P\{X=k\}=p^k(1-p)^{1-k},k=0,1,0<p<1 P{X=k}=pk(1−p)1−k,k=0,1,0<p<1
| X X X | 0 | 1 |
|---|---|---|
| p k p_k pk | 1 − p 1-p 1−p | p p p |
(0 — 1) 分布是经常遇到的一种分布, 用来描述只有两种对应结果的伯努利试验( 如成功与失败, 合格与不合格, 出现与不出现等).这些时候我们可以定义一个服从(0 — 1) 分布的随机变量:
X = { 0 , A 不 发 生 1 , A 发 生 X= \begin{cases} 0,A不发生\\ 1,A发生 \end{cases} X={0,A不发生1,A发生
二项分布
伯努利试验
设试验 E E E只有两种可能结果,A 及 A ‾ \overline{A} A, 则 E E E称为伯努利试验.若将试验 E E E独立地重复进行 n n n次, 则称这个试验为 n n n重伯努利试验.
伯努利试验是一个很重要的数学模型.
二项分布
在
n
n
n重伯努利试验中,若
P
(
A
)
=
p
,
P
(
A
‾
)
=
1
—
p
.
P(A)= p,P(\overline{A})= 1—p.
P(A)=p,P(A)=1—p.记X为
n
n
n次试验中事件A 发生的次数,显然
X
X
X是一个随机变量, 它的取值为$ 0,1,2,\dots,n.$它的分布律为
P
{
X
=
k
}
=
C
n
k
p
k
(
1
—
p
)
n
−
k
,
k
=
0
,
1
,
2
,
…
,
n
,
P\{X = k\}= C^k_np^k(1 —p)^{n-k} ,k = 0,1, 2, \dots,n,
P{X=k}=Cnkpk(1—p)n−k,k=0,1,2,…,n,
称 X服从参数为
n
,
p
n,p
n,p的二项分布,记为
X
∼
B
(
n
,
p
)
X\sim B(n,p)
X∼B(n,p)
二项分布与(0 — 1)分布有着密切关系
-
在二项分布中, 若 n = 1 , n=1, n=1, 二项分布就变成 (0 — 1) 分布;
-
在 n n n次伯努利试验中, 若只考虑某一次试验,比如第 i i i次试验, 可定义随机变量 X i X_i Xi如下:
X i = { 1 , 当 A i 发 生 时 0 , 当 A i ‾ 发 生 时 , i = 1 , 2 , ⋯ , n , X_i= \begin{cases} 1,当A_i发生时\\ 0,当\overline{A_i}发生时 \end{cases},i=1,2,\cdots,n, Xi={1,当Ai发生时0,当Ai发生时,i=1,2,⋯,n,X i X_i Xi服从( 0 — 1) 分 布. 对前面的 X X X,显然有 X = ∑ i = 1 n X i . X=\sum_{i=1}^{n}X_i. X=∑i=1nXi.而 X X X服从二项分布.所以说: n n n个服从(0-1)分布的且相互独立的随机变量 X i X_i Xi的和服从二项分布.
二项分布分布律中概率的最大值问题
1.取
k
0
=
[
(
n
+
1
)
p
]
,
P
{
X
=
k
0
}
k_0=[(n+1)p],P\{X=k_0\}
k0=[(n+1)p],P{X=k0}为分布律中的最大值([ ]为取整记号).
2.若
(
n
+
1
)
p
=
k
0
( n+ 1)p=k_0
(n+1)p=k0为 整 数, 则
P
{
X
=
k
0
}
=
P
{
X
=
k
0
−
1
}
P\{X = k0\}=P\{X=k_0-1\}
P{X=k0}=P{X=k0−1}同为分布律中的最大值.
泊松分布
泊松分布的定义
对于常数
λ
>
0
\lambda>0
λ>0,如果随机变量
X
X
X的分布律为
P
{
X
=
k
}
=
λ
k
e
k
k
!
,
k
=
0
,
1
,
2
,
⋯
,
P\{X=k\}=\frac {\lambda^ke^k}{k!},k=0,1,2,\cdots,
P{X=k}=k!λkek,k=0,1,2,⋯,
则称
X
X
X服从参数为 A 的泊松分布, 记为
X
∼
B
(
λ
)
X\sim B(\lambda)
X∼B(λ).
泊松定理
设有
X
∼
B
(
n
,
p
n
)
X\sim B(n,p_n)
X∼B(n,pn)和常数
λ
>
0
,
\lambda> 0,
λ>0,如果
n
p
n
=
λ
,
np_n=\lambda,
npn=λ,则
lim
n
→
∞
C
n
k
p
n
k
(
1
−
p
n
)
n
−
k
=
λ
k
e
−
λ
k
!
,
k
=
0
,
1
,
2
,
⋯
.
\lim_{n\to \infty} C^k_np^k_n(1-p_n)^{n-k}=\frac {\lambda^ke^{-\lambda}}{k!},k=0,1,2,\cdots.
n→∞limCnkpnk(1−pn)n−k=k!λke−λ,k=0,1,2,⋯.
①泊松定理说明,当 n → ∞ n\to \infty n→∞时,二项分布的极限分布为泊松分布.这从理论上说明了泊松分布的来源.
另一方面也表明 , 当 n n n很大很大时,二项分布可以用泊松分布近似代替.
实践中, 对 X ∼ B ( n , p ) X\sim B(n,p) X∼B(n,p)的情况, 当 n ≥ 50 , n p ≤ 10 n\geq50,np\leq10 n≥50,np≤10时,记 λ = n p . \lambda=np. λ=np.则有
C n k p k ( 1 − p ) n − k ≈ λ k e − λ k ! . C^k_np^k(1-p)^{n-k}\approx\frac {\lambda^ke^{-\lambda}}{k!}. Cnkpk(1−p)n−k≈k!λke−λ.② 具有泊松分布的随机变量在实际应用中是很多的, 如一本书一页中的印刷错误字数、 一段时间内电话用户对电话站的呼唤次数 、 电影院的观众数 , 等等. 泊松分布也是概率论中的一种重要分布.
超几何分布
超几何分布定义
KaTeX parse error: No such environment: align at position 57: …{N}^{n}} \begin{̲a̲l̲i̲g̲n̲}̲ ,k=0,1,2,\cdot…
随机变量 X 服从参数为$n, N,M 的 超 几 何 分 布 , 记 为 的超几何分布, 记为 的超几何分布,记为X\sim H( n,N,M)$
超几何分布的含义
有 N N N个球, 其中有 M M M个白球, N — M N—M N—M个黑球.从中取出 n n n个球, 取到 k k k个白球的概率.
几何分布
几何分布定义
P { X = k } = q k − 1 p , k = 1 , 2 , 3 , ⋯ , P \{ X = k \} = q^{k-1}p,k = 1,2,3,\cdots, P{X=k}=qk−1p,k=1,2,3,⋯, 其中 p ≥ 0 , q = 1 − p . p\geq0,q=1-p. p≥0,q=1−p.随机变量 X X X服从参数为 p p p的几何分布, 记为 X ∼ G ( p ) . X\sim G(p). X∼G(p).
几何分布的背景
每次 A 发生的概率为 p , p, p,而直到第 k k k次才出现A.
连续型随机变量及其概率分布
连续型随机变量
如果对于随机变量
X
X
X的分布函数
F
(
x
)
,
F(x),
F(x),存在非负函数
f
(
x
)
,
f(x),
f(x),使对于任意实数
x
x
x有
F
(
x
)
=
∫
−
∞
x
f
(
t
)
d
t
,
F(x)=\int_{-\infty}^{x}{f(t)dt},
F(x)=∫−∞xf(t)dt,
则称
X
X
X为连续型随机变量, 其中函数
f
(
x
)
f(x)
f(x)称为
X
X
X的概率密度函数, 简称概率密度.
概率密度的性质
-
f ( x ) ≥ 0 ; f(x)\geq 0; f(x)≥0;
-
∫ − ∞ + ∞ f ( x ) d x = 1 ; \int _{-\infty}^{+\infty}f(x)dx=1; ∫−∞+∞f(x)dx=1;
-
对于任意实数 x 1 , x 2 ( x 1 ≤ x 2 ) , x_1,x_2(x_1\leq x_2), x1,x2(x1≤x2),
KaTeX parse error: No such environment: equation at position 23: …<X<x_2\} \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ =F(x_2)-F(x_1)… -
f ( x ) f(x) f(x)若在点 x x x处连续,则有 F ′ ( x ) = f ( x ) . F'(x)=f(x). F′(x)=f(x).
常见连续型随机变量
均匀分布
均匀分布定义
若连续型随机变量
X
X
X具有概率密度
f
(
x
)
=
{
1
b
−
a
,
a<x< b
0
,
其他,
f(x)= \begin{cases} \frac{1}{b-a}, \text{a<x< b} \\ 0, \text{其他,} \end{cases}
f(x)={b−a1,a<x< b0,其他,
则称 X 在区间
(
a
,
b
)
(a,b)
(a,b)上服从均匀分布. 记为
X
∼
U
(
a
,
b
)
.
X\sim U(a,b).
X∼U(a,b).
X
X
X的分布函数为
F
(
x
)
=
{
0
,
x
<
a
,
1
b
−
a
,
a
≤
x
<
b
,
1
,
x
≥
b
F(x)= \begin{cases} 0, x<a,\\ \frac{1}{b-a},a\leq x< b,\\ 1, x\geq b \end{cases}
F(x)=⎩⎪⎨⎪⎧0,x<a,b−a1,a≤x<b,1,x≥b
均匀分布的性质
若
(
c
,
d
)
⊂
(
a
,
b
)
,
(c,d)\subset(a,b),
(c,d)⊂(a,b),则有
P
{
c
≤
X
≤
d
}
=
d
−
c
b
−
a
(
几
何
概
率
)
.
P\{c\leq X\leq d\}=\frac{d-c}{b-a}(几何概率).
P{c≤X≤d}=b−ad−c(几何概率).
指数分布
指数分布定义
若连续型随机变量
X
X
X 的概率密度为
f
(
x
)
=
{
λ
e
−
λ
x
,
x
>
0
,
0
,
x
≤
0.
f(x)= \begin{cases} \lambda e^{-\lambda x}, x>0,\\ 0,x\leq 0.\\ \end{cases}
f(x)={λe−λx,x>0,0,x≤0.
其中
λ
>
0
\lambda>0
λ>0为常数,则称
X
X
X服从参数为
λ
\lambda
λ的指数分布.
X X X的分布函数为 F ( x ) = { 0 , x > 0 , 1 − e − λ x , x ≤ 0. F(x)= \begin{cases} 0, x>0,\\ 1-e^{-\lambda x},x\leq 0.\\ \end{cases} F(x)={0,x>0,1−e−λx,x≤0.
指数分布的性质(无记忆性)
若
X
∼
E
(
λ
)
,
X\sim E(\lambda),
X∼E(λ),则对任何正数
x
,
x
0
,
x,x_0,
x,x0,必有
P
{
X
>
x
+
x
0
∣
X
>
x
0
}
=
P
{
X
>
x
}
.
P\{X>x+x_0\mid X>x_0\}=P\{X>x\}.
P{X>x+x0∣X>x0}=P{X>x}.
指数分布常用作描述一些电子元件的使用寿命,当 x > 0 x>0 x>0时 , P { X > x } = e − λ x ,P\{X>x\}=e^{-\lambda x} ,P{X>x}=e−λx
记住积分公式 ∫ 0 + ∞ x n e − x d x = n ! \int_{0}^{+\infty}{x^ne^{-x}dx}=n! ∫0+∞xne−xdx=n!对指数分布的计算很有帮助, 可能减少许多积分过程.
正态分布
正态分布定义
若连续型随机变量
X
X
X的概率密度函数为
f
(
x
)
=
1
2
π
σ
e
−
(
x
−
μ
)
2
2
σ
2
(
−
∞
<
x
<
+
∞
)
,
f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}(-\infty<x<+\infty),
f(x)=2πσ1e−2σ2(x−μ)2(−∞<x<+∞),
其中的正态分布
μ
\mu
μ与
σ
>
0
\sigma>0
σ>0都是常数,则称服从参数为
μ
\mu
μ与
σ
\sigma
σ的正态分布.简记为$X\sim N(\mu,\sigma^2). $
正态分布的性质
-
f ( x ) f(x) f(x)的图形关于 x = μ x =\mu x=μ对称;
-
当 x = μ x =\mu x=μ时, f ( μ ) = 1 2 π σ f(\mu)=\frac{1}{\sqrt{2\pi}\sigma} f(μ)=2πσ1为最大值.
X X X的分布函数为
F ( x ) = 1 2 π σ ∫ − ∞ x e − ( t − μ ) 2 2 σ 2 d t . F(x)=\frac{1}{\sqrt{2\pi}\sigma}\int _{-\infty}^{x}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt. F(x)=2πσ1∫−∞xe−2σ2(t−μ)2dt.
标准正态分布
当
μ
=
0
,
σ
=
1
\mu=0,\sigma=1
μ=0,σ=1时称随机变量
X
X
X服从标准正态分布.其概率密度和分布函数分别用
φ
(
x
)
,
Φ
(
x
)
\varphi(x),\Phi(x)
φ(x),Φ(x)表示,即有
φ
(
x
)
=
1
2
π
σ
e
−
t
2
2
,
Φ
(
x
)
=
1
2
π
σ
∫
−
∞
x
e
−
t
2
2
d
t
.
\varphi(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{t^2}{2}},\\ \Phi(x)=\frac{1}{\sqrt{2\pi}\sigma}\int _{-\infty}^{x}e^{-\frac{t^2}{2}}dt.
φ(x)=2πσ1e−2t2,Φ(x)=2πσ1∫−∞xe−2t2dt.
标准正态分布的性质
-
Φ ( − x ) = 1 − Φ ( x ) \Phi(-x)=1-\Phi(x) Φ(−x)=1−Φ(x)且 Φ ( 0 ) = 1 2 \Phi(0)=\frac {1}{2} Φ(0)=21此性质在计算和查表时都是很有用的.
-
若 X ∼ N ( μ , σ 2 ) , X\sim N(\mu,\sigma^2), X∼N(μ,σ2),则 Z = X − μ σ ∼ N ( 0 , 1 ) . Z=\frac{X-\mu}{\sigma}\sim N(0,1). Z=σX−μ∼N(0,1).
X X X得到 Z Z Z这种做法叫正态分布的标准化步骤.解决正态分布的计算问题最重要的, 首先要考虑的就是对 X X X进行标准化.
-
X ∼ N ( μ , σ 2 ) , X\sim N(\mu,\sigma^2), X∼N(μ,σ2), 则
P { a ≤ X ≤ b } = Φ ( b − μ σ ) − Φ ( a − μ σ ) . P\{a\leq X\leq b\}=\Phi(\frac{b-\mu}{\sigma})-\Phi(\frac{a-\mu}{\sigma}). P{a≤X≤b}=Φ(σb−μ)−Φ(σa−μ).
特例:
P
{
μ
−
k
σ
≤
X
≤
μ
+
k
σ
}
=
Φ
(
μ
+
k
σ
−
μ
σ
)
−
Φ
(
μ
−
k
σ
−
μ
σ
)
=
Φ
(
k
)
−
Φ
(
−
k
)
=
2
Φ
(
k
)
−
1
P\{\mu-k\sigma\leq X\leq \mu+k\sigma\}\\ =\Phi(\frac{\mu+k\sigma-\mu}{\sigma})-\Phi(\frac{\mu-k\sigma-\mu}{\sigma})\\ =\Phi(k)-\Phi(-k)\\ =2\Phi(k)-1
P{μ−kσ≤X≤μ+kσ}=Φ(σμ+kσ−μ)−Φ(σμ−kσ−μ)=Φ(k)−Φ(−k)=2Φ(k)−1
它的等价形式为
P
{
∣
X
−
μ
∣
≤
k
σ
}
=
2
Φ
(
k
)
−
1
P\{\mid X-\mu\mid\leq k\sigma\}=2\Phi(k)-1
P{∣X−μ∣≤kσ}=2Φ(k)−1
此概率值与
μ
,
σ
\mu,\sigma
μ,σ大小无关,只与
k
k
k的数值有关.
| k k k | P { ∣ X − μ ∣ ≤ k σ } P\{\mid X-\mu\mid\leq k\sigma\} P{∣X−μ∣≤kσ} |
|---|---|
| 1 | 0.6826 |
| 2 | 0.9544 |
| 3 | 0.9974 |
随机向量及其分布
二维随机变量
设 E E E是随机试验,样本空间为 Ω = { e } , \Omega=\{e\}, Ω={e},由 X = X ( e ) X=X(e) X=X(e)和 Y = Y ( e ) Y=Y(e) Y=Y(e)构成的一个向量$(X , Y) $叫做二维随机变量。
联合分布
二维随机变量的联合分布函数
设
(
X
,
Y
)
(X,Y)
(X,Y) 是二维随机变量
,
x
,
y
,x,y
,x,y是两个任意实数,则称定义在平面上的二元函数
P
{
X
≤
x
,
Y
≤
y
}
P\{X\leq x,Y\leq y\}
P{X≤x,Y≤y}为
(
X
,
Y
)
(X,Y)
(X,Y)的分布函数,或称为
X
X
X和
Y
Y
Y的联合分布函数,记作
F
(
x
,
y
)
,
F(x,y),
F(x,y),即
F
(
x
,
y
)
=
P
{
X
≤
x
,
Y
≤
y
}
.
F(x,y)=P\{X\leq x,Y\leq y\}.
F(x,y)=P{X≤x,Y≤y}.
F ( x , y ) F(x,y) F(x,y)的性质
-
0 ≤ F ( x , y ) ≤ 1 , 0\leq F(x,y)\leq 1, 0≤F(x,y)≤1,且 F ( − ∞ , y ) = F ( x , − ∞ ) = F ( − ∞ , − ∞ ) = 0 , F ( + ∞ , + ∞ ) = 1 F(-\infty,y)=F(x,-\infty)=F(-\infty,-\infty)=0,F(+\infty,+\infty)=1 F(−∞,y)=F(x,−∞)=F(−∞,−∞)=0,F(+∞,+∞)=1
-
F ( x , y ) F(x,y) F(x,y)是变量 x x x和 y y y的单调不减函数.
-
) F ( x , y ) = F ( x + 0 , y ) , F ( x , y ) = F ( x , y + 0 ) , F(x,y)=F(x+0,y),F(x,y)=F(x,y+0), F(x,y)=F(x+0,y),F(x,y)=F(x,y+0), 即 F ( x , y ) F(x,y) F(x,y)关于 x x x和 y y y都是右连续的.
-
对任意 ( x 1 , y 1 ) , ( x 2 , y 2 ) , (x_1,y_1),(x_2,y_2), (x1,y1),(x2,y2), 当 x 1 < x 2 , y 1 < y 2 x_1<x_2,y_1<y_2 x1<x2,y1<y2时有
P { x 1 < X ≤ x 2 , y 1 < Y ≤ y 2 } = F ( x 2 , y 2 ) − F ( x 1 , y 2 ) − F ( x 2 , y 1 ) + F ( x 1 , y 1 ) ≥ 0. P\{x_1<X\leq x_2,y_1<Y\leq y_2\}=F(x_2,y_2)-F(x_1,y_2)-F(x_2,y_1)+F(x_1,y_1)\geq0. P{x1<X≤x2,y1<Y≤y2}=F(x2,y2)−F(x1,y2)−F(x2,y1)+F(x1,y1)≥0.
联合分布律
若 ( X , Y ) (X,Y) (X,Y)所有可能取值为 ( x i , y j ) , i , j = 1 , 2 , ⋯ . (x_i,y_j),i,j=1,2,\cdots. (xi,yj),i,j=1,2,⋯.则称 ( X , Y ) (X,Y) (X,Y) 是离散型的随机变量.
称
P
{
X
=
x
i
,
Y
=
y
j
}
=
p
i
j
,
i
,
j
=
1
,
2
,
⋯
P\{X=x_i,Y=y_j\}=p_{ij},i,j=1,2,\cdots
P{X=xi,Y=yj}=pij,i,j=1,2,⋯为二维离散型随机变量
(
X
,
Y
)
(X,Y)
(X,Y) 的分布律,或随机变量
X
X
X和
Y
Y
Y的联合分布律.
也能用表格来表示
X
X
X和
Y
Y
Y的联合分布律, 如下表所示.
| Y / X Y/ X Y/X | x 1 x_1 x1 | x 2 x_2 x2 | ⋯ \cdots ⋯ | x i x_i xi | ⋯ \cdots ⋯ |
|---|---|---|---|---|---|
| y 1 y_1 y1 | p 11 p_{11} p11 | p 21 p_{21} p21 | ⋯ \cdots ⋯ | p i 1 p_{i1} pi1 | ⋯ \cdots ⋯ |
| y 2 y_2 y2 | p 12 p_{12} p12 | p 22 p_{22} p22 | ⋯ \cdots ⋯ | p i 2 p_{i2} pi2 | ⋯ \cdots ⋯ |
| ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ||
| y j y_j yj | p 1 j p_{1j} p1j | p 2 j p_{2j} p2j | ⋯ \cdots ⋯ | p i j p_{ij} pij | ⋯ \cdots ⋯ |
| ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ |
这里 p i j p_{ij} pij具有下列性质:
-
p i j ≥ 0 ( i , j = 1 , 2 , ⋯ ) ; p_{ij}\geq 0(i,j=1,2,\cdots); pij≥0(i,j=1,2,⋯);
-
∑ i ∑ j p i j = 1. \sum_i\sum_jp_{ij}=1. i∑j∑pij=1.
( X , Y ) (X,Y) (X,Y)的联合分布函数为
F ( x , y ) = ∑ x i ≤ x , y j ≤ y P { X = x i , Y = y j } . F(x,y)=\sum_{x_i\leq x,y_j\leq y}P\{X=x_i,Y=y_j\}. F(x,y)=xi≤x,yj≤y∑P{X=xi,Y=yj}.
联合概率密度
若存在非负的函数 f ( x , y ) f(x,y) f(x,y)使对任意有分布函数 F ( x , y ) = ∫ − ∞ x ∫ − ∞ y f ( u , v ) d u d v , F(x,y)=\int_{-\infty}^{x}\int_{-\infty}^{y}f(u,v)dudv, F(x,y)=∫−∞x∫−∞yf(u,v)dudv,则称 ( X , Y ) (X,Y) (X,Y)是连续型随机变量. f ( x , y ) f(x,y) f(x,y)称为 ( X , Y ) (X,Y) (X,Y)的联合概率密度.
联合密度的性质
-
f ( x , y ) ≥ 0. f(x,y)\geq0. f(x,y)≥0.
-
∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d y d x = F ( + ∞ , + ∞ ) = 1. \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)dydx=F(+\infty,+\infty)=1. ∫−∞+∞∫−∞+∞f(x,y)dydx=F(+∞,+∞)=1.
-
若 f ( x , y ) f(x,y) f(x,y)在点 ( x , y ) (x,y) (x,y)处连续, 则 ∂ 2 F ( x , y ) ∂ x ∂ y = f ( x , y ) . \frac{\partial^2F(x,y)}{\partial x\partial y}=f(x,y). ∂x∂y∂2F(x,y)=f(x,y).
-
设 G G G是 x O y xOy xOy平面上一个区域,则
P { ( X , Y ) ∈ G } = ∬ G f ( x , y ) d x d y P\{(X,Y)\in G\}=\iint_Gf(x,y)dxdy P{(X,Y)∈G}=∬Gf(x,y)dxdy
常见的二维随机变量的分布
二维均匀分布
如果二维随机变量
(
X
,
Y
)
(X,Y)
(X,Y)有概率密度
f
(
x
,
y
)
=
{
1
A
,
(
x
,
y
)
∈
G
,
0
,
其
他
.
f(x,y)= \begin{cases} \frac{1}{A},(x,y)\in G,\\ 0,其他. \end{cases}
f(x,y)={A1,(x,y)∈G,0,其他.
其中
G
G
G为平面有界区域
,
A
,A
,A为其面积,则称
(
X
,
Y
)
(X,Y)
(X,Y)在
G
G
G上服从二维均匀分布.
二维均匀分布的性质
在正矩形(矩形边与坐标轴平行)上,二维均匀分布的边缘分布是均匀分布,并且 X X X与 Y Y Y相互独立.
二维正态分布
如果二维随机变量
(
X
,
Y
)
(X,Y)
(X,Y)的概率密度为
f
(
x
,
y
)
=
1
2
π
σ
1
σ
2
1
−
ρ
2
e
x
p
{
−
1
2
(
1
−
ρ
2
)
[
(
x
−
μ
1
)
2
σ
1
2
−
2
ρ
(
x
−
μ
1
)
(
y
−
μ
2
)
σ
1
σ
2
+
(
y
−
μ
2
)
2
σ
2
2
]
}
(
−
∞
<
x
,
y
<
+
∞
)
,
f(x,y)=\frac{1}{2\pi\sigma_1\sigma_2 \sqrt{1-\rho^2}}exp\{-\frac{1}{2(1-\rho^2)}[\frac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}]\}(-\infty<x,y<+\infty),
f(x,y)=2πσ1σ21−ρ21exp{−2(1−ρ2)1[σ12(x−μ1)2−2ρσ1σ2(x−μ1)(y−μ2)+σ22(y−μ2)2]}(−∞<x,y<+∞),
其中
μ
1
,
μ
2
,
σ
1
,
σ
2
,
ρ
\mu_1,\mu_2,\sigma_1,\sigma_2,\rho
μ1,μ2,σ1,σ2,ρ均为常数,且
σ
1
>
0
,
σ
2
>
0
,
−
1
<
ρ
<
1
,
\sigma_1>0,\sigma_2>0,-1<\rho<1,
σ1>0,σ2>0,−1<ρ<1,则称
(
X
,
Y
)
(X,Y)
(X,Y)服从参数为
μ
1
,
μ
2
,
σ
1
,
σ
2
,
ρ
\mu_1,\mu_2,\sigma_1,\sigma_2,\rho
μ1,μ2,σ1,σ2,ρ的二维正态分布,记作
(
X
,
Y
)
∼
N
(
μ
1
,
σ
1
2
;
μ
2
,
σ
2
2
;
ρ
)
.
(X,Y)\sim N(\mu_1,\sigma_1^2;\mu_2,\sigma_2^2;\rho).
(X,Y)∼N(μ1,σ12;μ2,σ22;ρ).
特别,当
μ
1
=
μ
2
=
0
,
σ
1
=
σ
2
=
1
\mu_1=\mu_2=0,\sigma_1=\sigma_2=1
μ1=μ2=0,σ1=σ2=1时,则称
(
X
,
Y
)
(X,Y)
(X,Y)服从标准正态分布.
二维正态分布的性质
( X , Y ) ∼ N ( μ 1 , σ 1 2 ; μ 2 , σ 2 2 ; ρ ) ⇒ X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) (X,Y)\sim N(\mu_1,\sigma_1^2;\mu_2,\sigma_2^2;\rho)\Rightarrow X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2) (X,Y)∼N(μ1,σ12;μ2,σ22;ρ)⇒X∼N(μ1,σ12),Y∼N(μ2,σ22)
逆命题不成立.
边缘分布
边缘分布函数:
关于 X X X有:
F X ( x ) = P { X ≤ x } = P { X ≤ x , Y < + ∞ } ; F_X(x)=P\{X\leq x\}=P\{X\leq x,Y<+\infty\}; FX(x)=P{X≤x}=P{X≤x,Y<+∞};
关于 Y Y Y有
F Y ( y ) = P { Y ≤ y } = P { X < + ∞ , Y ≤ y } ; F_Y(y)=P\{Y\leq y\}=P\{X<+\infty,Y\leq y\}; FY(y)=P{Y≤y}=P{X<+∞,Y≤y};
由联合分布函数
F
(
x
,
y
)
F(x,y)
F(x,y)求边缘分布函数,有
F
X
(
x
)
=
F
(
x
,
+
∞
)
=
lim
y
→
+
∞
F
(
x
,
y
)
,
F
Y
(
y
)
=
F
(
+
∞
,
y
)
=
lim
x
→
+
∞
F
(
x
,
y
)
.
F_X(x)=F(x,+\infty)=\lim _{y\to+\infty}F(x,y),F_Y(y)=F(+\infty,y)=\lim _{x\to+\infty}F(x,y).
FX(x)=F(x,+∞)=y→+∞limF(x,y),FY(y)=F(+∞,y)=x→+∞limF(x,y).
离散型随机变量的边缘分布
边缘分布律
关于
X
X
X有:
P
{
X
=
x
i
}
=
∑
j
P
{
X
=
x
i
,
Y
=
y
j
}
=
∑
j
p
i
j
=
p
i
}
P\{X=x_i\}=\sum_jP\{X= x_i,Y=y_j\}=\sum_jp_ij=p_i\}
P{X=xi}=j∑P{X=xi,Y=yj}=j∑pij=pi}
关于
Y
Y
Y有
P
{
Y
=
y
j
}
=
∑
i
P
{
X
=
x
i
,
Y
=
y
j
}
=
∑
i
p
i
j
=
p
j
}
P\{Y= y_j\}=\sum_iP\{X= x_i,Y=y_j\}=\sum_ip_ij=p_j\}
P{Y=yj}=i∑P{X=xi,Y=yj}=i∑pij=pj}
边缘分布函数
关于
X
X
X有:
F
X
(
x
)
=
∑
x
i
≤
x
p
i
.
F_X(x)=\sum_{x_i\leq x}p_i.
FX(x)=xi≤x∑pi.
关于
Y
Y
Y有:
F
Y
(
y
)
=
∑
y
i
≤
y
p
j
.
F_Y(y)=\sum_{y_i\leq y}p_j.
FY(y)=yi≤y∑pj.
连续型随机变量的边缘分布
设 f ( x , y ) f(x,y) f(x,y)为联合密度函数 .
边缘密度函数
关于
X
X
X有:
f
X
(
x
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
y
,
f_X(x)=\int_{-\infty}^{+\infty}f(x,y)dy,
fX(x)=∫−∞+∞f(x,y)dy,
关于
Y
Y
Y有:
f
Y
(
y
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
x
.
f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)dx.
fY(y)=∫−∞+∞f(x,y)dx.
边缘分布函数
关于
X
X
X有:
F
X
(
x
)
=
∫
−
∞
x
f
X
(
x
)
d
x
=
∫
−
∞
x
∫
−
∞
+
∞
f
(
x
,
y
)
d
y
d
x
,
F_X(x)=\int_{-\infty}^{x}f_X(x)dx=\int_{-\infty}^{x}\int_{-\infty}^{+\infty}f(x,y)dydx,
FX(x)=∫−∞xfX(x)dx=∫−∞x∫−∞+∞f(x,y)dydx,
关于
Y
Y
Y有:
F
Y
(
y
)
=
∫
−
∞
y
f
Y
(
y
)
d
x
=
∫
−
∞
y
∫
−
∞
+
∞
f
(
x
,
y
)
d
x
d
y
.
F_Y(y)=\int_{-\infty}^{y}f_Y(y)dx=\int_{-\infty}^{y}\int_{-\infty}^{+\infty}f(x,y)dxdy.
FY(y)=∫−∞yfY(y)dx=∫−∞y∫−∞+∞f(x,y)dxdy.
条件分布
离散型随机变量的条件分布律
设
(
X
,
Y
)
(X,Y)
(X,Y)是二维离散型随机变量, 对于固定的
j
,
j,
j,若
P
{
Y
=
y
j
}
>
0
,
P\{Y=y_j\}>0,
P{Y=yj}>0,则称
p
X
∣
Y
(
i
∣
j
)
=
P
{
X
=
x
i
∣
Y
=
y
j
}
=
p
i
j
p
j
(
i
=
1
,
2
,
⋯
)
p_{X\mid Y}(i\mid j)=P\{X=x_i\mid Y=y_j\}=\frac {p_{ij}}{p_j}(i=1,2,\cdots)
pX∣Y(i∣j)=P{X=xi∣Y=yj}=pjpij(i=1,2,⋯)
为在
{
Y
=
y
j
}
\{Y=y_j\}
{Y=yj}条件下随机变量
X
X
X的条件分布律.
同样, 对于固定的
i
,
i,
i, 若
P
{
X
=
x
i
}
>
0
,
P\{X=x_i\}>0,
P{X=xi}>0,则称
p
Y
∣
X
(
j
∣
i
)
=
P
{
Y
=
y
j
∣
X
=
x
i
}
=
p
i
j
p
i
(
j
=
1
,
2
,
⋯
)
p_{Y\mid X}(j\mid i)=P\{Y=y_j\mid X=x_i \}=\frac {p_{ij}}{p_i}(j=1,2,\cdots)
pY∣X(j∣i)=P{Y=yj∣X=xi}=pipij(j=1,2,⋯)
为在
{
X
=
x
i
}
\{X=x_i\}
{X=xi}条件下随机变量
Y
Y
Y的条件分布律.
连续型随机变量的条件概率密度
设
(
X
,
Y
)
(X,Y)
(X,Y)是二维连续型随机变量,若
f
Y
(
y
)
>
0
,
f_Y(y)>0,
fY(y)>0,则称
p
X
∣
Y
(
x
∣
y
)
=
f
(
x
,
y
)
f
Y
(
y
)
(
−
∞
<
x
<
+
∞
)
p_{X\mid Y}(x\mid y)=\frac {f(x,y)}{f_Y(y)}(-\infty<x<+\infty)
pX∣Y(x∣y)=fY(y)f(x,y)(−∞<x<+∞)
为在
{
Y
=
y
}
\{Y=y\}
{Y=y}条件下随机变量
X
X
X的条件概率密度.
若
f
X
(
x
)
>
0
,
f_X(x)>0,
fX(x)>0,则称
p
Y
∣
X
(
y
∣
x
)
=
f
(
x
,
y
)
f
X
(
x
)
(
−
∞
<
y
<
+
∞
)
p_{Y\mid X}(y\mid x)=\frac {f(x,y)}{f_X(x)}(-\infty<y<+\infty)
pY∣X(y∣x)=fX(x)f(x,y)(−∞<y<+∞)
为在
{
X
=
x
}
\{X=x\}
{X=x}条件下随机变量
Y
Y
Y的条件概率密度.
随机变量的独立性
二维随机变量的独立性
若对任何都有 P { X ≤ x , Y ≤ y } = P { X ≤ x } P { Y ≤ y } , P\{X\leq x,Y\leq y\} = P\{X\leq x\}P\{Y\leq y\}, P{X≤x,Y≤y}=P{X≤x}P{Y≤y},即 F ( x , y ) = F X ( x ) F Y ( y ) , F( x , y ) = F_X( x )F_Y ( y ) , F(x,y)=FX(x)FY(y),则称随机变量 X X X和 Y Y Y是相互独立的.
独立性的判断方法 :
(1) 用分布函数:
X
,
Y
X,Y
X,Y相互独立的充分必要条件是在任何点
(
x
,
y
)
(x,y )
(x,y)都有
F
(
x
,
y
)
=
F
X
(
x
)
F
Y
(
y
)
;
F( x , y ) = F_X( x )F_Y ( y ) ;
F(x,y)=FX(x)FY(y);
(2) 对离散型随机变量:
X
,
Y
X,Y
X,Y相互独立的充分必要条件是对所有的
i
,
j
,
i,j,
i,j,都有
P
{
X
=
x
i
,
Y
=
y
j
}
=
P
{
X
=
x
i
}
P
{
Y
=
y
j
}
;
P\{X=x_i,Y=y_j\}=P\{X=x_i\}P\{Y=y_j\};
P{X=xi,Y=yj}=P{X=xi}P{Y=yj};
(3) 对连续型随机变量:
X , Y X,Y X,Y 相互独立的充分必要条件是对任何点 ( x , y ) (x,y) (x,y)都有 f ( x , y ) = f X ( x ) f Y ( y ) . f ( x , y ) = f_X( x ) f_Y ( y ) . f(x,y)=fX(x)fY(y).
多维随机变量的分布
联合分布函数为
F
(
x
1
,
x
2
,
⋯
,
x
n
)
=
P
{
X
1
≤
x
1
,
X
2
≤
x
2
,
⋯
,
X
n
≤
x
n
}
.
F(x_1,x_2,\cdots,x_n)=P\{X_1\leq x_1,X_2\leq x_2,\cdots,X_n\leq x_n\}.
F(x1,x2,⋯,xn)=P{X1≤x1,X2≤x2,⋯,Xn≤xn}.
边缘分布函数为
F
X
i
(
x
i
)
=
P
{
X
i
≤
x
i
}
=
F
(
+
∞
,
+
∞
,
⋯
,
x
i
,
⋯
,
+
∞
,
+
∞
)
,
(
i
=
1
,
2
,
⋯
,
n
)
.
F_{X_i}(x_i)=P\{X_i\leq x_i\}=F(+\infty,+\infty,\cdots,x_i,\cdots,+\infty,+\infty),(i=1,2,\cdots,n).
FXi(xi)=P{Xi≤xi}=F(+∞,+∞,⋯,xi,⋯,+∞,+∞),(i=1,2,⋯,n).
多维随机变量的独立性
若对所有
x
1
,
x
2
,
⋯
,
x
n
x_1,x_2,\cdots,x_n
x1,x2,⋯,xn都有
P
{
X
1
≤
x
1
,
X
2
≤
x
2
,
⋯
,
X
n
≤
x
n
}
=
P
{
X
1
≤
x
1
}
⋯
P
{
X
n
≤
x
n
}
,
P\{X_1\leq x_1,X_2\leq x_2,\cdots,X_n\leq x_n\}=P\{X_1\leq x_1\}\cdots P\{X_n\leq x_n\},
P{X1≤x1,X2≤x2,⋯,Xn≤xn}=P{X1≤x1}⋯P{Xn≤xn},
则称
X
1
,
X
2
,
⋯
,
X
n
X_1,X_2,\cdots,X_n
X1,X2,⋯,Xn是相互独立的.
X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn相互独立的判断条件:
-
X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn相互独立的充分必要条件是
F ( x 1 , x 2 , ⋯ , x n ) = F ( x 1 ) F ( x 2 ) ⋯ F ( x n ) . F(x_1,x_2,\cdots,x_n)=F(x_1)F(x_2)\cdots F(x_n). F(x1,x2,⋯,xn)=F(x1)F(x2)⋯F(xn).
-
对离散型随机变量: X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn相互独立的充分必要条件是
P { X 1 = x 1 , X 2 = x 2 , ⋯ , X n = x n } = P { X 1 = x 1 } ⋯ P { X n = x n } P\{X_1=x_1,X_2=x_2,\cdots,X_n=x_n\}=P\{X_1=x_1\}\cdots P\{X_n=x_n\} P{X1=x1,X2=x2,⋯,Xn=xn}=P{X1=x1}⋯P{Xn=xn}
-
对连续型随机变量: X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn相互独立的充分必要条件是
f ( x 1 , x 2 , ⋯ , x n ) = f X 1 ( x 1 ) f X 2 ( x 2 ) ⋅ f X n ( x n ) . f(x_1,x_2,\cdots,x_n)=f_{X_1}(x_1)f_{X_2}(x_2)\cdot f_{X_n}(x_n). f(x1,x2,⋯,xn)=fX1(x1)fX2(x2)⋅fXn(xn).
随机变量的函数的分布
这里要解决的问题是: 已知随机变量 X X X的分布 , Y = g ( X ) , g ,Y=g(X),g ,Y=g(X),g是连续函数,求随机变量 Y Y Y的分布.
离散型随机变量函数的分布
设随机变量 X 的 分布律为
P
{
X
=
x
k
}
=
p
k
,
k
=
1
,
2
,
⋯
,
P\{X=x_k\}=p_k,k=1,2,\cdots,
P{X=xk}=pk,k=1,2,⋯, 则当
Y
=
g
(
X
)
Y=g(X)
Y=g(X)的所有取值为:
y
j
(
j
=
1
,
2
,
⋯
)
y_j(j=1,2,\cdots)
yj(j=1,2,⋯)时, 随机变量
Y
Y
Y有分布律
P
{
Y
=
y
j
}
=
∑
g
(
x
i
)
=
y
j
P
{
X
=
x
i
}
.
P\{Y=y_j\}=\sum_{g(x_i)=y_j}P\{X=x_i\}.
P{Y=yj}=g(xi)=yj∑P{X=xi}.
连续型随机变量函数的分布
分布函数法
设随机
X
X
X的慨率密度函数为
f
X
(
x
)
(
−
∞
<
x
<
+
∞
)
,
f_X(x)(-\infty<x<+\infty),
fX(x)(−∞<x<+∞),那么
Y
=
g
(
X
)
Y=g(X)
Y=g(X)的分布函数为
F
Y
(
y
)
=
P
{
Y
≤
y
}
=
P
{
g
(
X
)
≤
y
}
=
∫
g
(
x
)
≤
y
f
X
(
x
)
d
x
,
F_Y(y)=P\{Y\leq y\}=P\{g(X)\leq y\}=\int_{g(x)\leq y}{f_X(x)dx},
FY(y)=P{Y≤y}=P{g(X)≤y}=∫g(x)≤yfX(x)dx,
其概率密度为
f
Y
(
y
)
=
F
Y
′
(
y
)
.
f_Y(y)=F'_Y(y).
fY(y)=FY′(y).
公式法
设随机变量
X
X
X具有概率密度函数
f
X
(
x
)
(
−
∞
<
x
<
+
∞
)
,
g
(
x
)
f_X(x)(-\infty<x<+\infty),g(x)
fX(x)(−∞<x<+∞),g(x)为
(
−
∞
<
x
<
+
∞
)
(-\infty<x<+\infty)
(−∞<x<+∞)内的严格单调的可导函数,则随机变量
Y
=
g
(
X
)
Y=g(X)
Y=g(X)的概率密度为
f
Y
(
y
)
=
{
f
X
[
h
(
y
)
]
∣
h
′
(
y
)
∣
,
α
<
y
<
β
0
,
其
他
.
f_Y(y)= \begin{cases} f_X[h(y)]\mid h'(y)\mid,\alpha<y<\beta\\ 0,其他.\\ \end{cases}
fY(y)={fX[h(y)]∣h′(y)∣,α<y<β0,其他.
其中
h
(
y
)
h(y)
h(y)是
g
(
x
)
g(x)
g(x)的反函数,
α
=
m
i
n
{
g
(
−
∞
)
,
g
(
+
∞
)
}
,
β
=
m
a
x
{
g
(
−
∞
)
,
g
(
+
∞
)
}
\alpha=min\{g(-\infty),g(+\infty)\},\\ \beta=max\{g(-\infty),g(+\infty)\}
α=min{g(−∞),g(+∞)},β=max{g(−∞),g(+∞)}
其分布函数为
F
Y
(
y
)
=
∫
−
∞
y
f
Y
(
t
)
d
t
.
F_Y(y)=\int^{y}_{-\infty}{f_Y(t)dt}.
FY(y)=∫−∞yfY(t)dt.
两个随机变量的函数的分布
设 ( X , Y ) (X,Y) (X,Y)为二维随机变量, z = g ( x , y ) z=g(x,y) z=g(x,y)为连续函数,则称 Z = g ( X , Y ) Z=g(X,Y) Z=g(X,Y)为二维随机变量 ( X , Y ) (X,Y) (X,Y)的函数.
显然
Z
Z
Z为一维随机变量,其分布函数为
F
Z
(
z
)
=
P
{
Z
≤
z
}
=
P
{
g
(
X
,
Y
)
≤
z
}
F_{Z}(z)=P\{Z\leq z\}=P\{g(X,Y)\leq z\}
FZ(z)=P{Z≤z}=P{g(X,Y)≤z}
若
(
X
,
Y
)
(X,Y)
(X,Y)为二维连续型随机变量,设其分布密度为
f
(
x
,
y
)
f(x,y)
f(x,y)则
Z
Z
Z的分布函数可表示为
F
Z
(
z
)
=
P
{
Z
≤
z
}
=
∬
g
(
x
,
y
)
≤
z
f
(
x
,
y
)
d
x
d
y
,
F_{Z}(z)=P\{Z\leq z\}=\iint_{g(x,y)\leq z}f(x,y)dxdy,
FZ(z)=P{Z≤z}=∬g(x,y)≤zf(x,y)dxdy,
由此得
Z
Z
Z的分布密度为
f
Z
(
z
)
=
d
F
Z
(
z
)
d
z
=
d
d
z
∬
g
(
x
,
y
)
≤
z
f
(
x
,
y
)
d
x
d
y
.
f_Z(z)=\frac{dF_Z(z)}{dz}=\frac{d}{dz}\iint_{g(x,y)\leq z}f(x,y)dxdy.
fZ(z)=dzdFZ(z)=dzd∬g(x,y)≤zf(x,y)dxdy.
Z = X + Y Z=X+Y Z=X+Y的分布
根据定义计算
F Z ( z ) = P { Z ≤ z } = P { X + Y ≤ z } F_{Z}(z)=P\{Z\leq z\}=P\{X+Y\leq z\} FZ(z)=P{Z≤z}=P{X+Y≤z}
分三种情况计算
-
X , Y X,Y X,Y是离散型:直接计算 Z 的分布律;
-
X , Y X,Y X,Y是连续型:利用定义计算 Z 的分布函数和分布密度,或根据 f Z ( z ) f_Z(z) fZ(z)作一重积分计算:
f Z ( z ) = ∫ − ∞ + ∞ f ( x , z − x ) d x . f_Z(z)=\int_{-\infty}^{+\infty}{f(x,z-x)dx}. fZ(z)=∫−∞+∞f(x,z−x)dx.
特别, 当 X X X 与 Y Y Y相互独立时,
f Z ( z ) = f X ∗ f Y = ∫ − ∞ + ∞ f X ( x ) ⋅ f Y ( z − x ) d x = ∫ − ∞ + ∞ f X ( z − y ) ⋅ f Y ( y ) d x ( 卷 积 公 式 ) . f_Z(z)=f_X*f_Y=\int_{-\infty}^{+\infty}{f_X(x)·f_Y(z-x)dx}=\int_{-\infty}^{+\infty}{f_X(z-y)·f_Y(y)dx}(卷积公式). fZ(z)=fX∗fY=∫−∞+∞fX(x)⋅fY(z−x)dx=∫−∞+∞fX(z−y)⋅fY(y)dx(卷积公式). -
X 是离散型, Y 是连续型:使用全概率公式.
关于正态分布的结论
两个独立的正态分布的仍为正态分布,即若 X ∼ N ( μ 1 , σ 1 2 ) , Y ∼ N ( μ 2 , σ 2 2 ) X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2) X∼N(μ1,σ12),Y∼N(μ2,σ22)则 Z = X + Y ∼ N ( μ 1 + μ 2 , σ 1 2 + σ 2 2 ) . Z=X+Y\sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2). Z=X+Y∼N(μ1+μ2,σ12+σ22).
典型例题
一维随机变量的分布函数


一维离散型随机变量的计算
二项分布与超几何分布
袋中装有6个大小相同的球,4个红色,2个白色.现从中连取5次,每次取一球,求取得红球的个数X的分布律:
(1)每次取出球观察颜色后,即放回袋中,拌匀后再取下一个球;
(2)每次取出球观察颜色后,不放回袋中,再取下一个球.
解:
(1) 随机变量X服从二项分布,则
X
∼
(
5
,
2
3
)
X\sim (5,\frac{2}{3})
X∼(5,32)故
P
{
X
=
k
}
=
C
5
k
(
2
3
)
k
(
1
3
)
5
−
k
,
k
=
0
,
1
,
2
,
3
,
4
,
5
,
P\{X = k\}= C^k_5(\frac{2}{3})^k(\frac{1}{3})^{5-k} ,k = 0,1, 2,3,4,5,
P{X=k}=C5k(32)k(31)5−k,k=0,1,2,3,4,5,
因此X的分布律为
| X X X | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| p k p_k pk | 1 243 \frac{1}{243} 2431 | 10 243 \frac{10}{243} 24310 | 40 243 \frac{40}{243} 24340 | 80 243 \frac{80}{243} 24380 | 80 243 \frac{80}{243} 24380 | 32 243 \frac{32}{243} 24332 |
(2)随机变量
X
X
X服从超几何分布,故
P
{
X
=
k
}
=
C
4
k
⋅
C
6
−
4
5
−
k
C
6
5
,
k
=
3
,
4
P\{X=k\}=\frac {C_4^k·C_{6-4}^{5-k}}{C _{6}^{5}},k=3,4
P{X=k}=C65C4k⋅C6−45−k,k=3,4
因此
X
X
X的分布律为
| X X X | 3 | 4 |
|---|---|---|
| p k p_k pk | 2 3 \frac{2}{3} 32 | 1 3 \frac{1}{3} 31 |
几何分布
一房间有3扇同样大小的窗子,其中只有一扇是打开的,有一只鸟自开着的窗子飞入房间,它只能从开着的窗子飞出去。鸟在房子里飞来飞去,试图飞出房间。鸟飞向各扇窗子都是随机的。
(1)假定鸟是没有记忆的,以X表示鸟为了飞出房间试飞的次数,求X的分布律;
(2)户主称,他养的鸟是有记忆的,它飞向任一窗子的尝试不多于一次,以Y表示这只聪明的鸟为了飞出房间试飞的次数,如户主所说是确实的,试求Y的分布律.
解:
(1) X服从几何分布,每次只能从开着的窗子飞出去,飞出去的概率为
1
3
,
\frac{1}{3},
31,因此
X
X
X的分布律为
P
{
X
=
k
}
=
(
2
3
)
k
−
1
1
3
(
k
=
1
,
2
,
⋯
)
.
P \{ X = k \} = (\frac{2}{3})^{k-1}\frac{1}{3}(k = 1,2,\cdots).
P{X=k}=(32)k−131(k=1,2,⋯).
(2)当鸟是有记忆的时,由题意,Y的可能取值为1,2.3.
Y=1,表明鸟从3扇窗子中选对了1扇,因对鸟面言.3扇窗是等可能的
,
P
{
Y
=
1
}
=
1
3
,P\{Y=1\}=\frac{1}{3}
,P{Y=1}=31
Y=2,表明鸟第1次试飞失败概率为
2
3
,
\frac{2}{3},
32,第二次,鸟舍弃已飞过的那扇窗,而从余下的一开一关两扇窗中选一,成功机会为
1
2
\frac{1}{2}
21,故
P
{
Y
=
2
}
=
2
3
×
1
2
=
1
3
P\{Y=2\}=\frac{2}{3}\times\frac{1}{2}=\frac{1}{3}
P{Y=2}=32×21=31
Y=3,表明鸟第1次试飞失败概率为
2
3
,
\frac{2}{3},
32,第二次,鸟舍弃已飞过的那扇窗,而从余下的一开一关两扇窗中选一,失败机会为
1
2
\frac{1}{2}
21,第三次从剩下的唯开着的窗子飞出,成功的概率为1.故
P
{
Y
=
3
}
=
2
3
×
1
2
×
1
=
1
3
P\{Y=3\}=\frac{2}{3}\times\frac{1}{2}\times1=\frac{1}{3}
P{Y=3}=32×21×1=31
因此Y的分布律为
| Y | 1 | 2 | 3 |
|---|---|---|---|
| p k p_k pk | 1 3 \frac{1}{3} 31 | 1 3 \frac{1}{3} 31 | 1 3 \frac{1}{3} 31 |
泊松分布
由商店过去的销售记录知道,某商品每月的销售数可以用参数λ=10的泊松分布来描述,为了以95%以上的把握保证不脱销,问商店在上一个月底至少应进某种商品多少件?
解:
设该商店每月销售某种商品X件,X服从参数λ= 10的泊松分布,故
P
{
X
=
k
}
=
1
0
k
e
k
k
!
,
k
=
0
,
1
,
2
,
⋯
,
P\{X=k\}=\frac {10 ^ke^k}{k!},k=0,1,2,\cdots,
P{X=k}=k!10kek,k=0,1,2,⋯,
设月底的进货为a件,则当
X
≤
a
X\leq a
X≤a时就不会脱销,因而按题意要求为
P
{
X
≤
a
}
≥
0.95
,
P\{X\leq a\}\geq 0.95,
P{X≤a}≥0.95,
即
∑
k
=
0
a
1
0
k
e
−
10
k
!
>
0.95
,
\sum_{k=0}^{a}\frac {10 ^ke^{-10}}{k!}>0.95,
k=0∑ak!10ke−10>0.95,
由泊松分布表可得
∑
k
=
0
14
1
0
k
e
−
10
k
!
≈
0.9166
<
0.95
,
∑
k
=
0
15
1
0
k
e
−
10
k
!
≈
0.9513
>
0.95.
\sum_{k=0}^{14}\frac {10 ^ke^{-10}}{k!}\approx 0.9166<0.95,\\ \sum_{k=0}^{15}\frac {10 ^ke^{-10}}{k!}\approx 0.9513>0.95.
k=0∑14k!10ke−10≈0.9166<0.95,k=0∑15k!10ke−10≈0.9513>0.95.
于是,这家商店只要在月底进货某种商品15件(假定上个月没存货),就可以95%以上的把握保证这种商品在下个月内不脱销.
一维连续型随机变量的计算
均匀分布
设X在[2,5]上服从均匀分布,求X的取值小于3的概率。
总长度:3
小于3的长度:1
P ( X 的 取 值 小 于 3 ) P_{(X的取值小于3)} P(X的取值小于3)= 1 3 \frac{1}{3} 31
指数分布
某种电子元件的使用寿命X (单位:小时)服从
λ
=
1
/
2000
\lambda=1/2000
λ=1/2000的指数分布。
求:(1)一个元件能正常使用1000小时以上的概率;
(2)一个元件能正常使用1000小时到2000小时之间的概率。
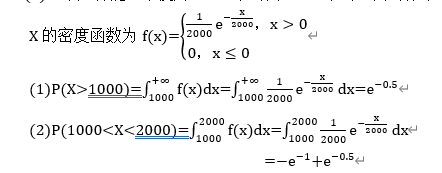
正态分布

一维随机变量函数的分布
公式法

分布函数法


























 277
277











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








