
1.参数假设检验
在总体分布已知的情况下,对分布中未知参数的检验。
(1)相关基本概念
零假设/原假设与对立假设/备择假设:


任务:根据样本作出是否接受H0
复合假设与简单假设:

否定域/拒绝域与接受域:



假设原假设成立,即a=a0,那么其与样本均值应该差的不太多,如果差的太多,那么就与原先的共有与样本均值应该差的不太多的常识矛盾,那么应该拒绝这个假设(是一种概率意义上的反证法)
对于H0:a=a0 H1:a>a0
如何确定其拒绝域:
即为
从到
从n维判断变换到了一维判断,当判断区间为一个时,称为单侧检验,当判断区间为两个时,称为双侧检验。
检验函数和检验统计量:

检验函数也即为示性函数,
在上述例子中即为,
在有时,并不是单纯的取0/1,由于样本的随机性,在拒绝域和接受域之间的一小部分值会有较大的争议,此时即为随机化检验


两类错误和功效函数:
由于样本的随机性,总会犯错误

第一类错误:P(落在拒绝域|为真) =
弃真错误
第二类错误:P(落在接受域|为真)/P(落在接受域|
为假) 取伪错误
例:


在某一具体场合下,两种错误只会犯一个
我们希望两个错误都尽可能小 ,但事实上是做不到的。
为了将两个错误统一起来,引入功效函数:

对于两个概率的理解:


对于功效函数曲线的理解:
当未知参数落在拒绝域时,此时可能犯第一类错误,且概率等于,应使其值尽可能低,当未知参数落在接受域时,且概率等于
此时可能犯第二类错误,应使其值尽可能大。
例:

功效函数就是拒绝域的概率
黄色区域为第二类错误的概率,非黄色区域为第一类错误的概率
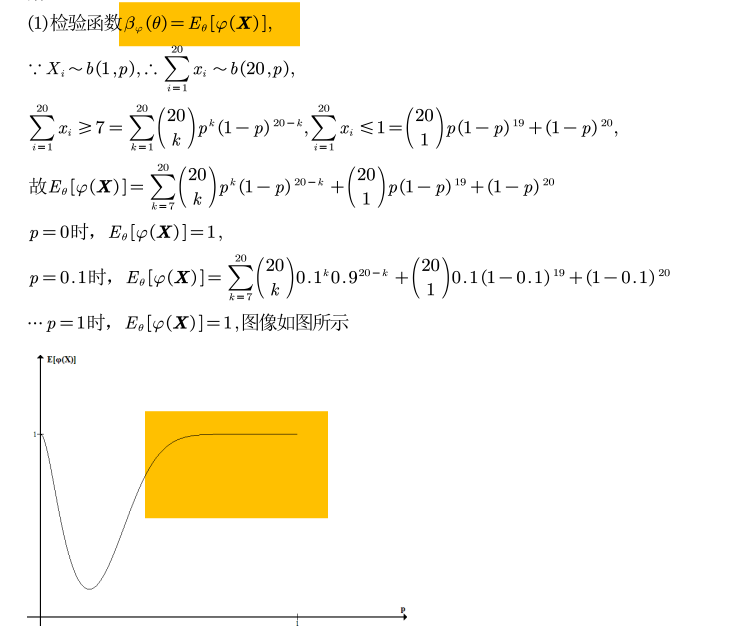
检验的水平就是第一类错误发生的概率,即为p=0.2时的取值

例:


例:

未知参数的值需要讨论
例:


未知参数是自变量
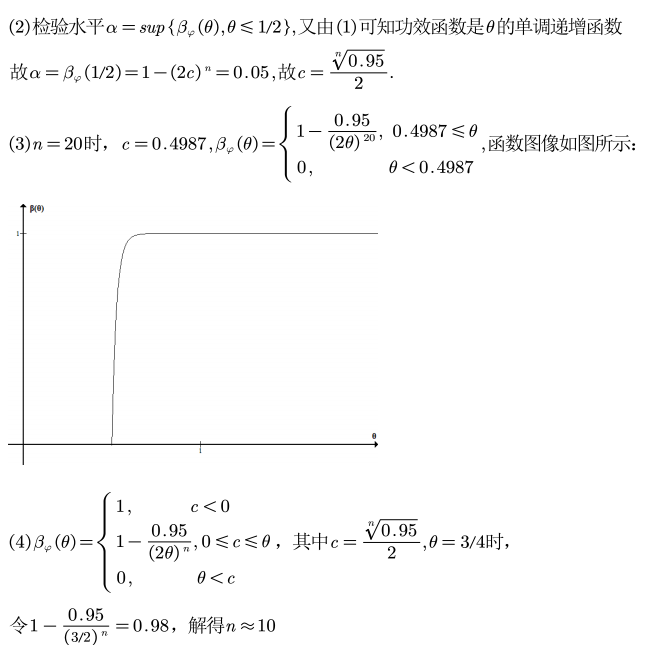
基于我们希望两个错误都尽可能小 ,但事实上是做不到的现实,提出:
Neyman-Pearson原则


类比于区间估计:在保证选取的区间能够套住未知参数的前提下保证区间的长度尽可能短
保护原假设:



一些说明:
(1)检验函数:拒绝域时取值为1,接受域时取值为0
(2)功效函数:检验函数的期望,即为拒绝域的概率,此时未知参数属于全体未知参数空间
(3)功效曲线:由此有关于未知参数的功效曲线,理想的形状是在接受域时尽可能大,在拒绝域时尽可能小
2.求解假设检验问题的一般步骤

对于(1)H0与H1的选择:(很重要,具有实际意义)
a.把久经考验的事实放在H0(保护原假设)
b.把你希望得到的结论放在H1,希望通过拒绝H0得到你的结论(由于是保护原假设,那么否定原假设需要充足的证据,也就是说接受H1有充足的证据)
c.等号放在H0
否定原假设比较靠谱因为一般会有95%或90%的把握,因而否定原假设需要更多的证据,而由于保护原假设的存在,当没有充足证据拒绝原假设时就认为接受原假设。


例:


对于(2)检验统计量的建立:
a.有枢轴变量转换成的统计量(即先找未知参数的比较好的点估计,然后构造枢轴量,然后将未知参数赋予已知值)
b.似然比统计量
例:

3.正态总体的假设检验
——基于枢轴变量转化的统计量
包括两个流程:
a.假设检验流程(概率意义上的反证法)
b.假设检验方法的评价(Neyman-Pearson原则)
对于a:
假设H0为真,那么就可以使用H0的条件,由此构造统计量(将枢轴变量中的未知参数已知化),判断样本统计值是否落在拒绝域上(由于的值通常很小,小概率事件不会发生),做出判断。
对于b:
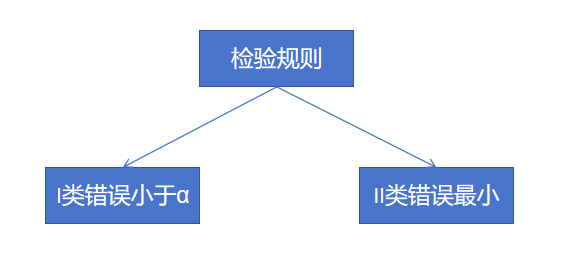
具体步骤为由I类错误条件得到d值,由II类错误判断是否最小
下面的具体例子:
对于a过程分别为:
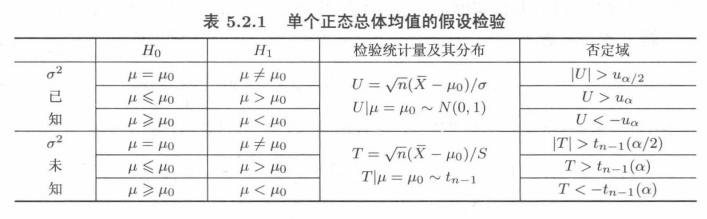
(1)单个正态总体的均值检验
和区间估计一模一样
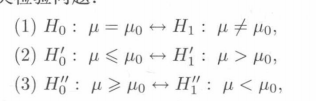
对于第一个是
计算的值,判断是否在区间中
对于后两个是:
,其中d根据情况不同
对于置信限:只需要将改为
即可,
即为:
上限:
下限:
此时总体不必正态。
双正态总体是同样的。
对于b过程:
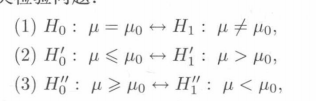
第一个:

对于第二个:


显著性水平的全覆盖
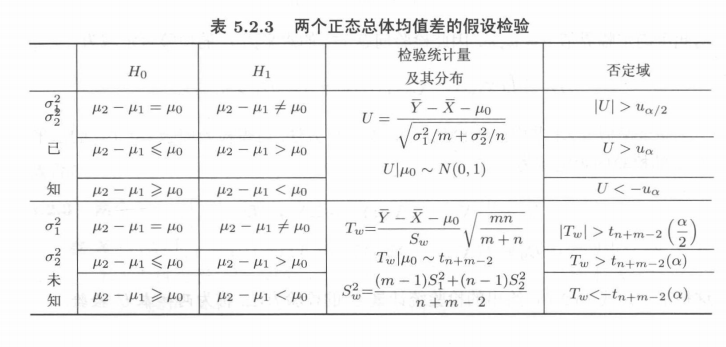
(2)双正态总体的均值差检验

(1)均值差的区间估计
最后一种情况总体不必正态。
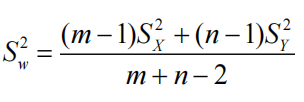
成组检验和成对检验:
成组检验指随机选取两组均值比较
成对检验:令,x与y之间只有某项指标不同,其余条件相同
例:
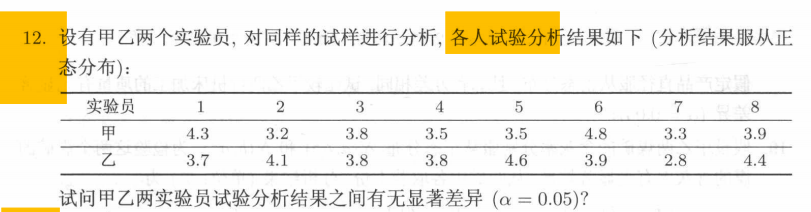

例:

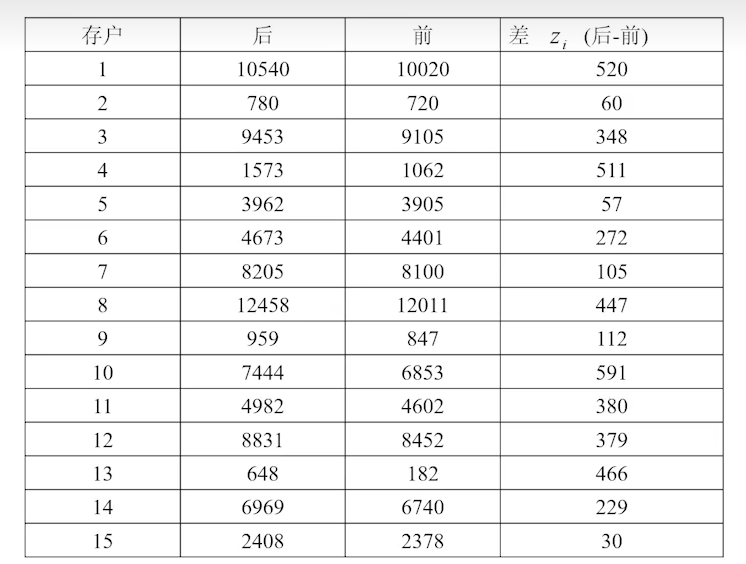


合理选择成对/成组,对于结论有重要的意义
(3)单正态总体的方差检验
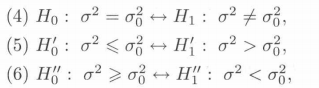
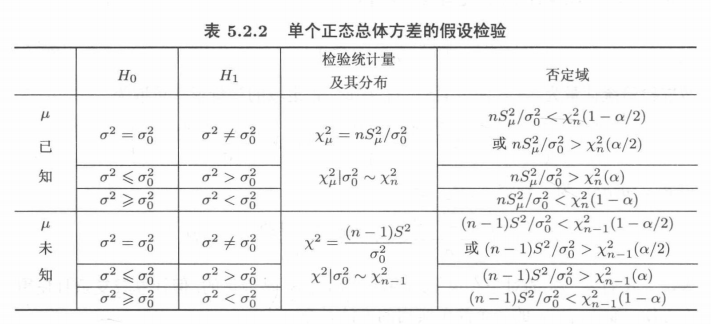
(4)双正态总体的方差比检验
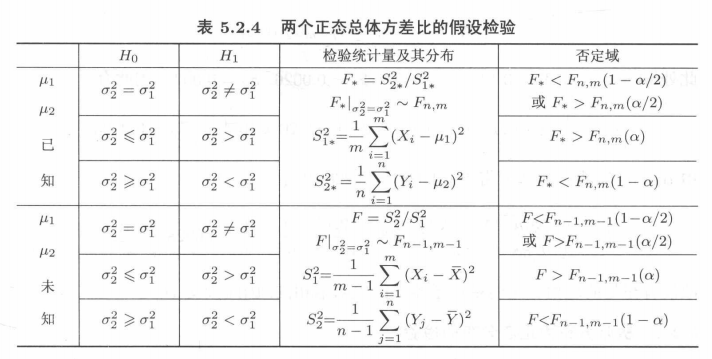
(5)大样本检验







例:

possion分布——>中心极限定理
不知道分布——>Behrens-Fisher方法
例:


先检验方差再在检验的基础上判断是否有差异
补充:Behrens-Fisher方法:
大样本方法就是将方差换成样本方差
小样本方法:

例:



例:

大样本:
例:
![]()


例:
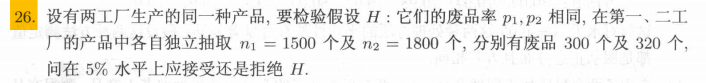

4.似然比检验


定义:


步骤:

单调函数:
,将T(X)看作一个整体
例1:



一类错误/ 显著性水平:

关于单调性的解释:注意是统计量,此时的
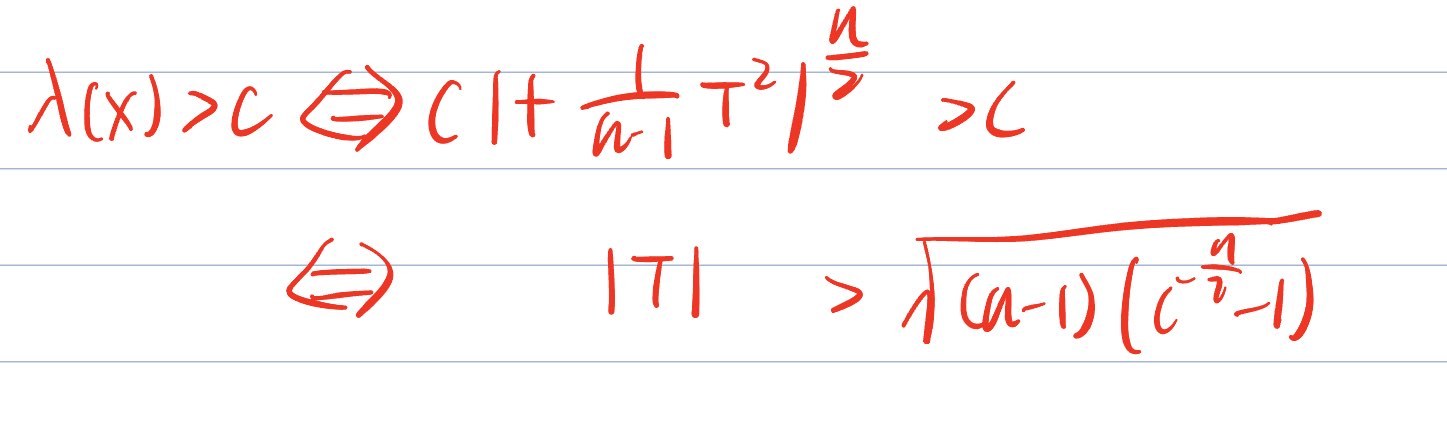
例2:



例3:

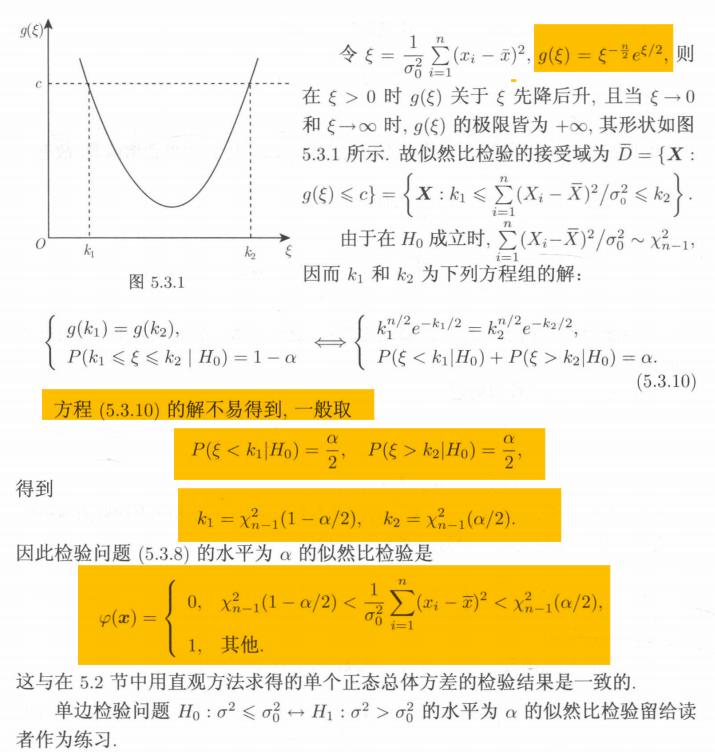
说明:
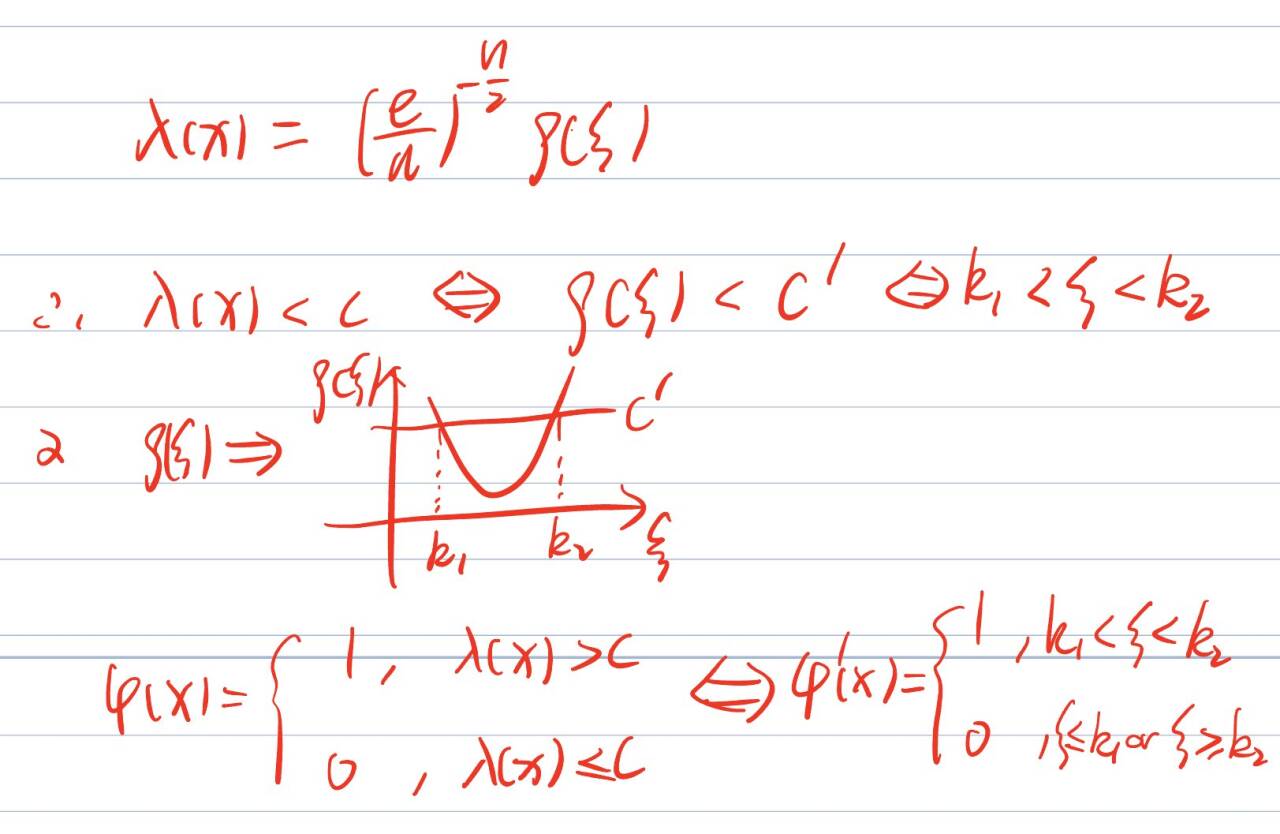
例4:均匀分布



例5:指数分布
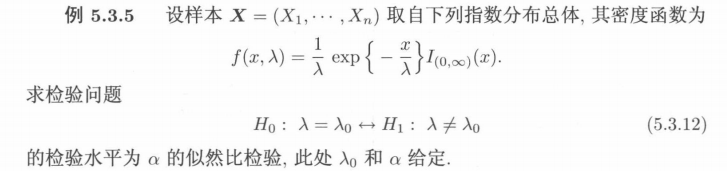

例:





说明在整个定义域内是单调不减的
大样本:(Wilks定理)



5.一致最优检验(UMPT)
定义:


即若为功效函数为凸函数,则在一个点取得最大值,即若当对立假设为一个点时,此时第二类错误最小,而当对立假设不为一个点时,就不是对于所有点取得最小,当与对立假设参数无关时可以。
这个定义的关键是对于对立参数空间的所有参数都要成立
由此,Neyman-Pearson引理:

例1:


也就是说既然与对立假设参数无关,那么我取任意一个都可以,他们的全体就可以组成一个不等式。
例2:


例3:


例:


6.由NP引理求一致最优检验(UMPT)
将H0和H1都变成复合检验:


证明基本思想:
对于对立假设,功效函数与对立假设参数无关
对于原假设,证明功效函数是关于假设参数的一个增函数,由此可以实现显著水平的全覆盖


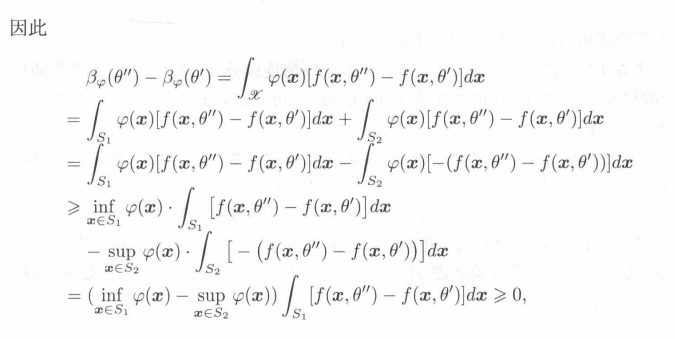



例1:


例2:



例:

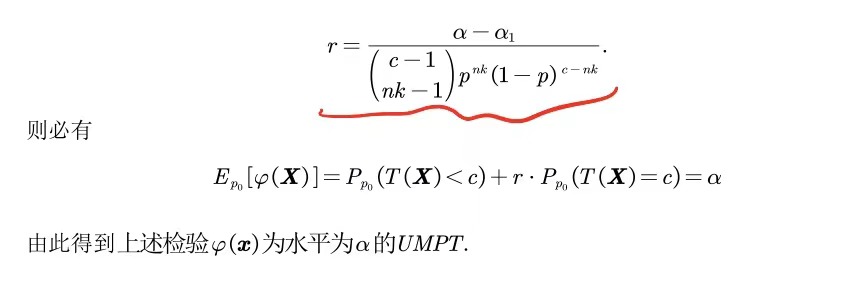
例:两个正态总体
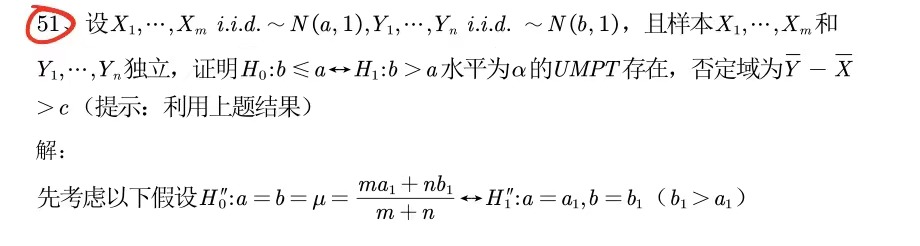

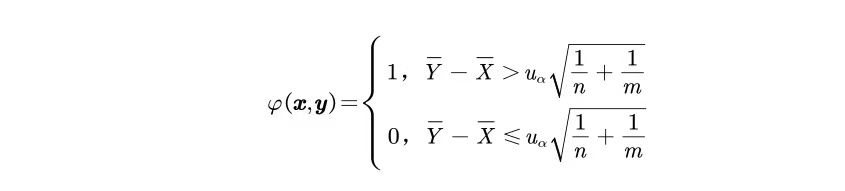
例:
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








