统计是一门艺术（点估计）

m00—

已于 2024-06-23 16:07:28 修改

阅读量1k

点赞数 31

文章标签：学习笔记

于 2024-06-23 10:27:19 首次发布

本文链接：https://blog.csdn.net/m0_46240166/article/details/139631250

版权

1 点估计

1.1 点估计理解（point estimate）

总体 $\sim f(x,\theta_{1},...,\theta_{k})$ ，样本 $X=(X_{1},...,X_{n}),\theta=(\theta_{1},...,\theta_{k})$ 属于参数空间

一般 $\theta$ 未知，要由样本对 $\theta$ 作一个估计，或对 $g(\theta )$ 作一个估计，这种估计称为点估计

通常用 $\hat{g}(X)$ 记为 $g(\theta )$ 的一个点估计。

1.2 点估计的方法

（1）矩估计：

就是用样本矩来代替总体矩，当然有好有坏

设 $X=(X_{1},...,X_{n})$ 为总体的一个简单随机样本， $k\in N$ ，

分别称 $a_{nk} = \frac{1}{n}\sum_{i=1}^{n}X_{i}^{k}$ ， $m_{nk} = \frac{1}{n}\sum_{i=1}^{n}(X_{i}-\bar{X})^{k}$

为k阶样本原点矩和k阶样本中心矩.

记 $\alpha_{k} = EX^{k},\mu_{k} = E(X-\alpha_{1})^{k}$

为什么能用矩估计？原理？

根据大数定理，当 $n\rightarrow\infty$ （ $n\geq 30$ ）时，

$a_{nk}\overset{P}{\rightarrow}\alpha_{k}$ ， $m_{nk}\overset{P}{\rightarrow}\mu_{k}$ ,所以当样本数据量到达一定数目时，就可以用样本的矩来估计总体的矩，从而估计一系列矩的函数。

定义：在应用中用样本矩来代替总体矩，得到的估计称为矩估计,

前提：未知参数可以使用总体矩来表示

核心：样本矩来代替总体矩

区别：不同的样本矩表达的效果不同

设 $g(\theta ) = G(\alpha_{1},...,\alpha_{k},\mu_{1},...,\mu_{l})$ ,则 $\hat{g}(X) = G(a_{n1},...,a_{nk},m_{n1},...,m_{nl})$ ，称为 $g(\theta )$ 的一个矩估计

例1. 总体均值a，总体方差为 $\sigma^{2}$ ,则 $\hat{a}_{M} = EX = \bar{X}$ ， $\hat{\sigma}^{2}_{M} = m_{nl}$ ， $\tilde{\sigma}^{2}_{M} = S^{2}$

故未知参数的矩估计不唯一，那么那种估计是最好的？

低阶矩比高阶矩好

例2.总体 $\sim P(\lambda )$ ， $EX = \lambda ,Var(X)=\lambda$

则 $\hat{\lambda }_{M1}=\bar{X},\hat{\lambda }_{M2}=S^{2}$ ,故未知参数的矩估计不唯一

例3.总体 $\sim U(\theta_{1},\theta_{2})$ ,求 $\hat{\theta }_{M1},\hat{\theta }_{M2}$

因为 $EX=\frac{1}{2}(\theta _{1}+\theta _{2})$ ，

$Var(X) = \frac{1}{12}(\theta_{1}-\theta_{2})^{2}$

用 $\bar{X}$ 代替EX， $S^{2}$ 代替 $Var(X)$ 可以反解出结果。

例4.总体 $\sim f(x,\theta ) = \frac{1}{\pi(1+(x-\theta)^2)}$ ,EX不存在，所以未知参数的矩估计不存在

统计量与统计值（由样本表示具有样本的性质）

偏度系数/峰度系数/变异系数，对于一个总体是否服从正态分布，可以先计算其系数，若与正态分布的值相差不大，则可认为是正态分布

例5.(X,Y)协方差及相关系数的矩估计

$Cov(X,Y) = E(X-EX)(Y-EY)$

$\rho_{xy} = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}$

用样本数据取估计总体的协方差和相关系数

广义矩估计

总而言之：矩估计即使用样本矩代替总体矩，至于准不准，需要后面的判断

$\sqrt{DX}=\sqrt{DX_{1}}$

(2)极大似然估计（MLE）

概率密度函数的两种形态：

a.当未知参数固定，就是概率函数

b.当随机变量取值固定，此时就是似然函数

原理：既然随机变量取值固定，那么这些变量取这些值的概率就应该为1，那么变化未知参数，使得概率密度取值最大，这个未知参数就是我们想要的。似然函数表达了在给定样本下，概率结构的变化

例1.标志重捕法

定义：

那么接下来就是求极值的问题了，此时的变量只有未知参数，所以一般而言是对未知参数求导

对于简单随机样本 $X=(X_{1},...,X_{n})$ ,若总体 $\sim f(x,\theta )$ ,则 $X=(X_{1},...,X_{n})\sim \prod_{i=1}^{n}f(x_{i},\theta )$ ,

记 $L(x_{1},...,x_{n},\theta )=L(x,\theta )$ ,

$lnL(x,\theta )=\prod_{i=1}^{n}lnf(x_{i},\theta )$

定理： $\prod_{i=1}^{n}f(x_{i},\theta )$ 有指数族的自然形式， $lnL(x,\theta )$ 的驻点在参数空间内部，则该驻点唯一，且为极大似然估计（这里需要继续看）

例1：

例2：

如果矩估计和极大似然都不可以做，那么用什么估计？

例3：

对于定数截尾，可以使用次序统计量的概率密度函数来进行判断，次序统计量是实际观察到的量

对于定时结尾如何判断？什么是实际观察到的量？

设 $y_{i}$ 为第i个产品的寿命，所以服从指数分布 $\sim exp(\lambda )$

则 $X_{i}=\left\{\begin{matrix} Y_{i}, &Y_{i}<T & \\ T,& Y_{i}\geq T& \end{matrix}\right.$ ,故 $X_{i}$ 为观测到的量

即为 $X_{i} = Y_{i}I_{(Y_{i}<T)}+TI_{(Y_{i}\geq T)}$

则 $f(t,\lambda ) = f_{y}(t,\lambda )I_{(t<T)}+e^{\lambda T}I_{(t=T)}$ $=\lambda e^{-\lambda t}I_{(t<T)}+e^{\lambda T}I_{(t=T)}$

设有r个T之前失效，n-r个T之后失效，则似然函数为

$L(t,\lambda ) = \lambda^{r}e^{(t_{1}+...+t_{r})\lambda }e^{-(n-r)\lambda T }$

求解即可，同时这也是既非离散也非连续的情况

例4：

总而言之，MLE就是在样本取值固定的情况下，使得取这些值的概率最大，因为此时只有未知参数是不确定的，所以就成了对未知参数求导，求得未知参数的极值。

1.3 点估计的评价标准

（1）无偏性

对未知参数的估计是由统计量来表示的，统计量是随机变量，故存在均值和方差

含义：没有系统偏差

尽管某一次可能会吃亏，但长远来看是相当的

总体的均值为a，总体方差为 $\sigma^{2}$ ， $a=\bar{X},\hat{\sigma^{2}}=m_{n2},\hat{\sigma^{2}_{1}}=S^{2}$

$E\bar{X}=a,Em_{n2}=\frac{n-1}{n}\sigma^{2}$ ——>修正为 $S^{2}$

$a_{nk}=\frac{1}{n}\sum_{i=1}^{n}X_{i}^{k}\rightarrow Ea_{nk}=\alpha_{k}$

$m_{nk}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\bar{X})^{k}$ ， $Em_{nk}\neq \mu_{k}$

样本n阶原点矩是总体n阶原点矩的无偏估计，如果未知参数等于总体n阶原点矩，那么就是未知参数的无偏估计

样本n阶中点矩通常不是总体n阶中点矩的无偏估计

在独立同分布的条件下，k阶原点矩是易求的，如何求k阶中心矩？

以三阶中心距为例：

$m_{n3}=\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\bar{X})^{3}$ ， $Em_{n3}=E\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\bar{X})^{3}$ ,标准化：

$Em_{n3}=E\frac{1}{n}\sum_{i=1}^{n}((X_{i}-a)-(\bar{X}-a))^{3}$

令 $Y_{i}=X_{i}-a$

则化简为： $Em_{n3}=E\frac{1}{n}\sum_{i=1}^{n}(Y_{i}-\bar{Y})^{3}$

$Em_{n3}=E\frac{1}{n}\sum_{i=1}^{n}(Y_{i}^{3}-3Y_{i}^{2}\bar{Y}+3Y_{i}\bar{Y}^{2}-\bar{Y}^{3})$ $=\frac{1}{n}(n\mu_{3}-3\mu_{3}+3nE\bar{Y}^{3}-En\bar{Y}^{3})$

PS: $\mu_{3} = E\frac{1}{n}\sum_{i=1}^{n}Y_{i}^{2}\bar{Y}=E\frac{1}{n}\sum_{i=1}^{n}Y_{1}^{2}\bar{Y}=EY_{1}^{2}\bar{Y}=EY_{1}^{3}=\mu_{3}$

最终： $Em_{n3}=\mu_{3}(1-\frac{3}{n})+2nE\bar{Y}^{3}=\frac{(n-1)(n-2)}{n^{2}}\mu_{3}$

$E\bar{Y}^{3}=\frac{1}{n^{3}}n\mu_{3}$ 可以展开，单阶项可以通过刚才的标准化归为0

可以修正为： $\hat{\mu_{3}}=\frac{n^{2}}{(n-1)(n-2)}m_{n3}$

X i.i.d ,EX=0, $E(X_{1}+...+X_{n})^{k}\sim n^{\frac{k}{2}}$ （需要看看）

例1：总体 $\sim P(\lambda )$

$\hat{\lambda_{1}}=\bar{X},\hat{\lambda_{2}}=S^{2}$

$E\bar{X}=ES^{2}=\lambda$

两个都是无偏估计，那么谁最好？这时比方差，一般低阶矩的方差小

例2：gamma分布的可加性

例3 总体 $X\sim B(1,\theta )$ ,求 $\hat{\theta }_{M}$ 和 $\hat{\theta(1-\theta)}_{M}$

对于两点分布：

$EX=\theta$ ， $\hat{\theta }_{M}=\bar{X}$ ，由于 $E\bar{X}=\theta$ ,所以无偏

$\hat{\theta(1-\theta)}_{M}=\bar{X}(1-\bar{X})$ ，由于 $E\bar{X}(1-\bar{X})= \frac{n-1}{n}\theta (1-\theta )$ ，系统偏小

和的期望是无条件的

注意n3服从二项分布

（2）有效性

如果的波动程度小，那么一次取样就越接近均值

一般低阶矩更加有效

（3）大样本性质

小样本性质：n固定

大样本性质：n在变化，（ $n\rightarrow \infty$ ）

a.渐进无偏估计

b.相合性

正态分布正交变换的性质

弱大数定律的连续函数形式

柯尔莫哥洛夫强大数定律：

均方相合估计：

c.相合渐进正态估计

如何证明？

若n个独立同分布变量的和，则使用弱大数定律，如辛钦大数定律

若不是n个独立同分布变量的和，则使用切比雪夫不等式，概率计算公式

1.4 一致最小方差无偏估计（UMVUE）

是无偏估计就是可估的，不是无偏估计就是不可估的

无偏估计不是总是存在的

均方误差： $E_{\theta }(\hat{g}(X)-g(\theta ))^{2}$ ，兼顾方差和均值的一种衡量标准

$E_{\theta }(\hat{g}(X)-g(\theta ))^{2}=E[(\hat{g}(X)-E\hat{g}(X))+(E\hat{g}(X)-g(\theta ))]^{2}$

$=Var\hat{g}(X)+(E\hat{g}(X)-g(\theta ))^{2}+2E[(\hat{g}(X)-E\hat{g}(X)(E\hat{g}(X)-g(\theta))]$

$=Var\hat{g}(X)+(E\hat{g}(X)-g(\theta ))^{2}$

TIPS： $E\hat{g}(X)-g(\theta)$ 为一个常数，故 $E[(\hat{g}(X)-E\hat{g}(X)]=0$

使这两部分都小的情况很难找到，那么退而求其次，使得后一项达到0，即为在无偏估计的情况下

一致最小均方误差估计通常很难找到，那么退而求其次，使得后一项达到0，即为在无偏估计的情况下，此时比较的标准只有方差：

因为后一项为0，所以只需要比较前一项即D

引理：

从引理中可以得到：

对于任意的 $g(\theta )$ 的无偏估计 $\hat{g}(X)$ ,若T为充分统计量，则

1） $E(\hat{g}|T)=h(T)$ 仍为 $g(\theta )$ 的无偏估计

2）若 $\hat{g}(X)$ 不是T的函数，则可以找到T的函数h(T)，使h(T)为 $g(\theta )$ 的无偏估计，且方差不超过 $Var\hat{g}(X)$

综上UMVUE只需要在T的函数中寻找。

如何寻找一致最小方差无偏估计：

$\theta$ 可估: $\exists \hat{g}(X),E\hat{g}(X)=\theta$

$g(\theta)$ 可估： $\exists \hat{g}_{1}(X),E\hat{g}_{1}(X) = g(\theta)$

（1）Lehmann-Scheffe定理

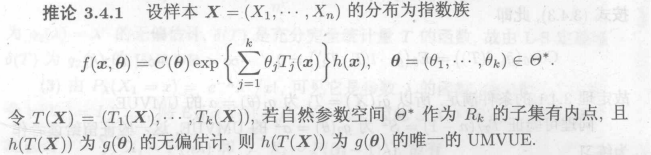
指数族的自然形式——>完全充分统计量

步骤：

先找充分完全统计量T

再找 $g(\theta )$ 的无偏估计，设为 $\varphi (X)$ :

$\varphi (X)$ 可以表达为T的函数，则直接使用

$\varphi (X)$ 不是T的函数，则将其修正为T的函数，修正后函数直接使用， $h(T)=E(\varphi (X)|T)$

那么怎么去找 $\varphi (X)$ 是 $g(\theta )$ 的无偏估计？

a.先求充分完全统计量的期望，方差，二阶原点矩，然后凑出待求变量

b.生成函数

c.直接用定义

例如：

如果充分完全统计量包括两个以上，那么 $\varphi (X)$ 只需是其中一个，那么就是T的函数

例1 :是T的函数

例2 ：是T的函数

另一种解法：

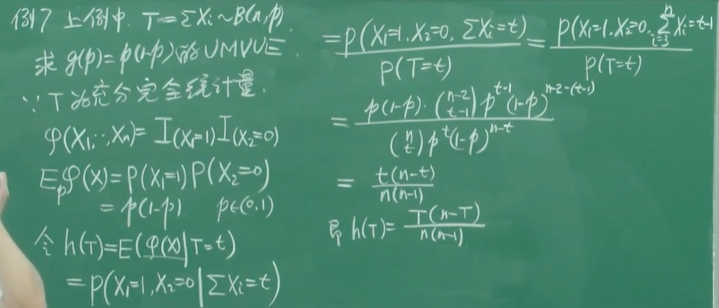
例3：找完全充分统计量的无偏估计

对于r.v. X,生成函数为：

$p(X=k) = p_{k}$

$h(t) = Et^{X} = \sum t^{k}p_{k}$

$h^{'}(t)|_{t=1} = EXt^{X-1} = EX$

$h^{''}(t)|_{t=1} = EX(X-1)t^{X-2} = EX(X-1)$

$h^{r}(t)|_{t=1} = EX(X-1)...(X-r+1)$

对于泊松分布：

$h(t) = \sum t^{k}\frac{e^{-\lambda}\lambda^{k}}{k!}=e^{\lambda(t-1)}$

$h^{''}(t)|_{t=1} = \lambda^{2}$

$h^{r}(t)|_{t=1} = \lambda^{r}$

$T=\sum X$ 为完全充分统计量

因为 $E_{\lambda }T(T-1)(T-2)...(T-r+1)=(n\lambda )^{r}$

所以 $\frac{T(T-1)...(T-r+1)}{n^{r}}$ 是 $\lambda^{r}$ 的无偏估计

例4：

另加：求 $g_{1}(\lambda ) = 1-e^{-x_{0}\lambda }$ 的UMVUE

$E\hat{g}(X) = 1-e^{-\lambda x_{0}}$

$h(T)=E(\hat{g}(X)|T=t)=P(X_{1}\leq x_{0}|T=t)I_{x_{0}\leq t}$ $=\int_{0}^{\infty }f_{X_{1}|T}(x_{1}|t)dx$

$f_{X_{1}|t}(x_{1}|t) = \frac{f(X_{1} = x_{1},\sum X_{i}=t)}{f(\sum X_{i}=t)}$

例5：

另外：求 $g_{1}(\theta )=\frac{a}{\sigma ^{2}}$ 的UMVUE

T1与T2是独立的

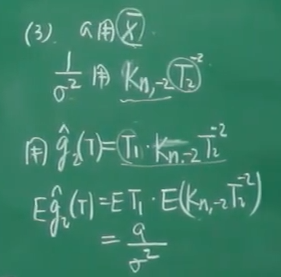
（2）零无偏估计法

为什么要选用充分统计量？因为包含了全部信息

1.5 Cramer-Rao不等式

达到C-R下界的一定是最小方差无偏估计，但满足C-R不等式的通常很少，一般来说C-R下界会偏小。

$I(\theta )$ 从总体中计算

（1）单参数C-R不等式

有了上面的正则条件才能证明，统计学的函数空间的投影理论？

指数族：未知参数*exp{未知参数与样本组合}*不含未知参数

Fisher信息函数：

（2）多参数的C-R不等式

效率和有效估计：

拉格朗日乘数法：（条件极值）

怎么求UMVUE：

a.L-S定理

b.零无偏估计

c.拉格朗日乘数法（约束条件是期望无偏）

2.多元函数求极值

极值：

最值：

无条件极值：

注：极值点存在于驻点和不可导的点

条件极值：

几种题目：有界区域：分为无条件极值和条件极值，所有极值比较大小即为最值

无条件极值求区域内部不包含边界，条件极值求边界，综合起来就是最值

矩阵的正定性：(二阶连续可导就是为了保证对称)

hassen矩阵求解极值：

3.期望和方差的性质

和的期望可以无条件拆开，乘积的期望需要独立才能拆开

4.线性空间

5.数理统计的线性空间描述

投影？

6.Be分布与Γ分布

指数分布和卡方分布是特殊形式的Γ分布

0-1区间的均匀分布是特殊的Be分布

https://zhuanlan.zhihu.com/p/69606875https://zhuanlan.zhihu.com/p/69606875