[深度学习]激活函数(Sigmoid等)、前向传播、反向传播和梯度优化；optimizer.zero_grad(), loss.backward(), optimizer.step()的作用及原理

用Matt Mazur的例子，来简单告诉读者推导过程吧（其实就是链式）！

先初始化权重和偏置量，得到如下效果：

一、激活函数

1.1 什么是激活函数？

激活函数可以分为线性激活函数（线性方程控制输入到输出的映射，如f(x)=x等）以及非线性激活函数（非线性方程控制输入到输出的映射，比如Sigmoid、Tanh、ReLU、LReLU、PReLU、Swish 等）

激活函数是向神经网络中引入非线性因素，通过激活函数神经网络就可以拟合各种曲线。激活函数又可以分为饱和激活函数（Saturated Neurons）和非饱和函数（One-sided Saturations）。Sigmoid和Tanh是饱和激活函数，而ReLU以及其变种为非饱和激活函数。非饱和激活函数主要有如下优势：

1. 非饱和激活函数可以解决梯度消失问题。
2. 非饱和激活函数可以加速收敛。

1.2 常见的激活函数

1.2.1 Sigmoid函数

$Sigmoid函数也叫Logistic函数$，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。sigmoid是一个十分常见的激活函数，函数的表达式如下：

图像类似一个S形曲线：

• Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到1，因此它对每个神经元的输出进行了归一化；
• 函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率；
• 但是Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦，也就是说，Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时，输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此，这些神经元的权重不会更新。此外，与此类神经元相连的神经元的权重也更新得很慢。该问题叫作$梯度消失$。

1.2.2 ReLU激活函数

ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题，在目前的深度神经网络中被广泛使用。ReLU函数本质上是一个斜坡（ramp）函数，公式及函数图像如下：

图像：

• 当输入为正时，导数为1，一定程度上改善了梯度消失问题，加速梯度下降的收敛速度；
• 计算速度快得多。ReLU 函数中只存在线性关系，因此它的计算速度比 sigmoid 和 tanh 更快。
  被认为具有生物学合理性（Biological Plausibility）,比如单侧抑制、宽兴奋边界（即兴奋程度可以非常高）

1.2.3 Softmax激活函数

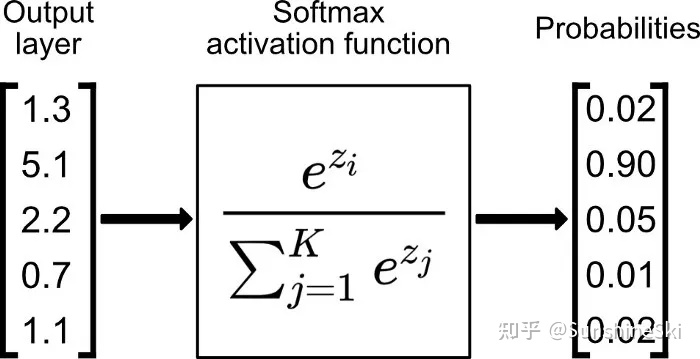
Softmax 是用于多类分类问题的激活函数，在多类分类问题中，超过两个类标签则需要类成员关系。对于长度为 K 的任意实向量，Softmax 可以将其压缩为长度为 K，值在（0，1）范围内，并且向量中元素的总和为 1 的实向量。函数表达式如下：

图像：

作用示例：$一般用来放在网络最后输出各类别概率值$

Softmax 激活函数的不足：

• 在零点不可微；
• 负输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。

1.2.4 其他激活函数参考深度学习笔记：如何理解激活函数？（附常用激活函数）

二、前向传播推理inference计算示例

• 计算neth1=w*i+b
• 通过激活函数计算outh1
• 计算下一层的neth2、通过下一层的激活函数
• 计算误差Etotal

三、反向传播backward计算示例

• 链式法则：计算Etotal关于w5的偏导，其实=计算Etotal关于outh1的偏导 * outh1关于neth1的偏导 * neth1关于w5的偏导
• 分别对应三个函数：误差函数、激活函数、y=w*i+b

通过相同的步骤就可以更新所有的w：

参考：

• 深度学习—反向传播的具体案例
• Matt Mazur
• 【深度学习理论】纯公式手推+代码撸——神经网络的反向传播+梯度下降

四、梯度优化

4.1 如何最小化一个任意函数？

仔细观察成本函数，其形式为Y=X²。在笛卡尔坐标系中，这是一个抛物线方程，用图形表示如下：

为了最小化上面的函数，需要找到一个x，函数在该点能产生小值Y，即图中的红点。

由于这是一个二维图像，因此很容易找到其最小值，但是在$维度比较大$的情况下，情况会更加复杂。对于这种情况，需要设计一种算法来定位最小值，该算法称为梯度下降算法(Gradient Descent)。

梯度下降是优化模型的方法中最流行的算法之一，也是迄今为止优化神经网络的最常用方法。它本质上是一种迭代优化算法，用于查找函数的最小值。

4.2 表示

假设你是沿着下面的图表走，目前位于曲线’绿’点处，而目标是到达最小值，即红点位置，但你是无法看到该最低点。

可能采取的行动：

• 可能向上或向下；
• 如果决定走哪条路，可能会采取更大的步伐或小的步伐来到达目的地；

在下图中，在绿点处绘制切线，如果向上移动，就将远离最小值，反之亦然。此外，切线也能让我们感觉到斜坡的陡峭程度：

蓝点处的斜率比绿点处的斜率低，这意味着从蓝点到绿点所需的步长要小得多。
参考：图解梯度下降背后的数学原理

4.3 深度学习中的梯度优化

在机器学习的核心内容就是把数据喂给一个人工设计的模型，然后让模型自动的“学习”，从而优化模型自身的各种参数，最终使得在某一组参数下该模型能够最佳的匹配该学习任务。那么这个“学习”的过程就是机器学习算法的关键。梯度下降法就是实现该“学习”过程的一种最常见的方式，尤其是在深度学习(神经网络)模型中，BP反向传播方法的核心就是对每层的权重参数不断使用梯度下降来进行优化。

参考：梯度下降法 —— 经典的优化方法

4.4 不同的优化器Optimization（从SGD到Adam至Lookahead…）

4.4.1 随机梯度下降法SGD

批梯度下降法（stochastic gradient descent）是指使用每一条数据来计算梯度值更新参数：

通常，随机梯度下降法相比于批梯度下降法具有更快的速度，可用于在线学习，SGD以高方差频繁地更新，因此容易出现下列剧烈波动的情况。

4.4.2 其他优化器详解参考史上最详细的梯度下降优化算法介绍（从SGD到Adam至Lookahead）

五、理解optimizer.zero_grad(), loss.backward(), optimizer.step()的作用及原理

在用pytorch训练模型时，通常会在遍历epochs的过程中依次用到optimizer.zero_grad(),loss.backward()和optimizer.step()三个函数，如下所示：

model = MyModel()
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.001, momentum=0.9, weight_decay=1e-4)
 
for epoch in range(1, epochs):
    for i, (inputs, labels) in enumerate(train_loader):
        output= model(inputs)
        loss = criterion(output, labels)
        
        # compute gradient and do SGD step
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

总得来说，在学习pytorch的时候注意到，对于每个batch大都执行了这三种操作。这三个函数的作用是

• 先将每一个batsize的梯度归零（optimizer.zero_grad()），
• 然后反向传播计算得到$loss关于每个参数的梯度值$（loss.backward()）【此处和具体的loss值无关，和其梯度有关】，
• 最后通过梯度下降执行一步参数更新（optimizer.step()）

参考：理解optimizer.zero_grad(), loss.backward(), optimizer.step()的作用及原理
参考：[pytorch] torch代码解析 为什么要使用optimizer.zero_grad()