随笔——基尔霍夫热辐射定律中灰体发射率和吸收率相等的推导逻辑

m0_46416432

已于 2023-11-29 15:02:17 修改

阅读量5.9k

点赞数 5

分类专栏：想写就写文章标签：热力学

于 2023-03-10 11:48:01 首次发布

本文链接：https://blog.csdn.net/m0_46416432/article/details/127185270

版权

想写就写专栏收录该内容

6 篇文章

订阅专栏

本文灵感来源于最近我在重新学传热学的课程时，对灰体的发射率和吸收率相等的推导过程阅读时觉得书上有些语焉不详，于是用自己的语言解释了下。

首先，让我们来看课本上关于基尔霍夫（Kirchhoff）定律的定义和推导过程。

两块无限靠近的无限大平行平板之间的辐射换热（系统处于热平衡），如图所示：

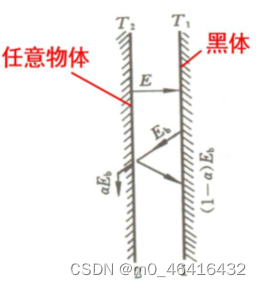
板1为黑体表面，其辐射力、吸收比和表面温度分别为 $E_b,\alpha_b,T_1$ ，其中 $\alpha_b=1$

板2为任意物体的表面，其辐射力、吸收比和表面温度分别为 $E ,\alpha ,T_2$

板2的能量收支差额：板2自身单位面积在单位时间内发射出的能量 $E$ ，这份能量投射在黑体表面1上被全部吸收。同时，黑体表面1辐射出的能量为 $E_b$ ，这份能量落到板2上时，只被吸收 $\alpha E_b$ ，其余部分 $(1-\alpha)E_b$ 被反射回板1，被黑体表面1全部吸收。

板2的能量收支差额即两板间传热的热流密度：

$q=E-\alpha E_b$

当处于热平衡状态时，有 $q=0$ ，即可得

$\alpha =\frac{E}{E_b}=\varepsilon$

其中， $\varepsilon$ 为物体的发射率。回顾推导过程，发射率 $\varepsilon$ 的定义需要两个严格的条件才能推导出：

①这个物体接收到的辐射必须是来自黑体的；

②物体处于热平衡状态。

这样得到的 $\varepsilon$ 值在实际应用过程中非常受限，为了使发射率 $\varepsilon$ 的定义式还能应用于非热平衡状态，投入辐射不是来自黑体的常规工程应用，就需要人为地来创造条件了。这一部分就很刻意：

①吸收比 $\alpha (\lambda )$ 是和波长有关的数，所以将研究的对象假设为灰体来解除这种限制，实际过程中的物体也大多可以视作灰体。进一步地，可以假设为漫射灰体，也解除了角度对吸收比的限制。即存在 $\alpha (\lambda )=Constant$ ;

②发射率 $\varepsilon (T)$ 是一个物性参数，这里的T是物体自己的温度。物性参数也就是只与自身有关而与外界条件无关；

③在某一温度 $T_0$ 下，先假设温度 $T_0$ 的物体接收到了来自温度 $T_0$ 的黑体的投入辐射，因此有 $\alpha(T_{0 black})=\varepsilon(T_{0 object})$ ,当改变温度 $T_0$ 的大小时，该式仍成立。因为 $\varepsilon (T)$ 是物性参数，所以有 $\alpha(T_{0 black})=\varepsilon(T_{0 object})=\alpha(T_{0 object})$ ，这样， $\alpha$ 也变成了一个只和自身温度条件有关的物性参数了。