顺序高斯消元法、列主元高斯消元法、追赶法、Jacobi迭代法、Gauss-Seidel迭代法解方程组与比较（Matlab编程版）

对于给定方程组

想要解出x，可以使用顺序高斯消元法、列主元高斯消元法、追赶法、Jacobi迭代法、Gauss-Seidel迭代法等求解出。同时，为了比较各种方法的差异性，选用误差（知道准确解的前提下）、计算时间，迭代次数这三个指标来评价不同方法的优劣。

为了使所有方法能解同一系数矩阵，这里举例选用三对角矩阵，实际除追赶法外其他计算方法使用于所有矩阵。

1.预处理系数矩阵A

给定的系数矩阵A，是三对角矩阵且是稀疏矩阵，有三种不同的阶数。先计算出系数矩阵的条件数cond(A)，判断是否为病态方程。

当cond(A)>>1时可以认定A为病态方程，本文取1000为判断为病态方程的标准。当A为病态方程时，说明解方程过程中的扰动与舍入的误差会被放大到十分影响解的准确性的程度。

2.顺序高斯消元法

顺序高斯消元法主要通过逐次消去未知数的方法把原来方程组Ax=b化为与其等价的三角方程组。主要方法如下：进行第k次消元，设第k-1次步计算已经完成，即此时方程组已变为A(k)x=b(k)，设a(k)kk≠0，计算乘数mik有

用-mik乘以A(k)x=b(k)中的第k个方程在加上第i个方程，消去第k+1个方程直到第n个方程的未知数xk，进一步得到A(k +1)x=b(k+1)。其中，A(k +1)元素的计算公式为

继续这一过程，直到完成第n-1次消元，得到A(n)x=b(n)，完成消元步骤。

为了求解出x，还需对消元后的矩阵A(n)进行回代过程。求解公式为

function [x,t] = gauss_elimination(A, b)

% A: 系数矩阵
% b: 增广矩阵最后一列
% x: 方程组的解
tic%计算程序运行时间开始
n = length(b);
    for k = 1:n-1
        for i = k+1:n
            factor = A(i,k) / A(k,k);
            A(i,k:n) = A(i,k:n) - factor * A(k,k:n);
            b(i) = b(i) - factor * b(k);
        end
    end

    x = zeros(n,1);
    x(n)=b(n)/A(n,n);
    for i = n-1:-1:1
        x(i) = (b(i) - A(i,i+1:n) * x(i+1:n)) / A(i,i);
    end
t=toc%计算程序运行时间终止




end

3.列主元高斯消元法

列主元高斯消元法是对顺序高斯消元法的优化，主要考虑到在消元过程中可能会出现a(k)kk=0的情况，或者a(k)kk≠0但很小，作为除数会放大传递误差，最后使得计算的解不可靠。因此在每次消元前，增加按列选主元素的步骤。第k步选主元素，即确定ik，使

消元后回代解出x，步骤与顺序高斯消元法一致。

function  [x,t]=lie_gauss_elimination(A,b)


%准备工作：获取方程组的信息；
tic
    n=length(b);                 %获取矩阵的行和列；
    x=zeros(n,1);

    %按列选主元；
    for k=1:n-1               
     max=abs(A(k,k));      
        r=k;                  
        for i=k+1:n          
            if max<abs(A(i,k))
                max=abs(A(i,k));
                r=i;          
            end
        end
    
    
        %换行；要将主对角元的行的元素全部与列主元最大元素所在行的元素交换；
        if r~=k                
            for c=k:n            
                a(c)=A(k,c);      
                A(k,c)=A(r,c);    
                A(r,c)=a(c);     
            end                  
            d=b(k);               
            b(k)=b(r);            
            b(r)=d;               
        end
    
        %消元；就是把主对角元下面的元素全部划为0---目的是要系数矩阵A化为一个上三角的系数矩阵；
        for i=k+1:n
            factor = A(i,k) / A(k,k);
            A(i,k:n) = A(i,k:n) - factor * A(k,k:n);
            b(i) = b(i) - factor * b(k);
            A(i,k)=0;
        end

        %回代求解；此时已经化为上三角型的系数矩阵了；主要从下往上代入求解即可；
        x(n)=b(n)/A(n,n);
        for i=n-1:(-1):1
            sum=0;
            for j=i+1:n
                sum=sum+A(i,j)*x(j);
            end
            x(i)=(b(i)-sum)/A(i,i);
        end

    end
t=toc
end

4.追赶法

追赶法只用于解三对角方程组，且系数矩阵为对角占优矩阵。可以直接利用矩阵的直接三角分解法进行计算。其关键量α、β的计算公式如下

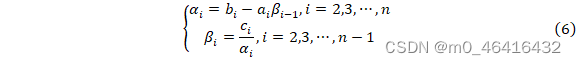
此外，α1=b1，β1=c1/α1，γi=ai。最后，将α作为L的主对角元素，γ作为L的次对角元素，β作为U的次对角元素，即可得到LU分解中的变量值。在编程中，计算x的程序命令为

x=invbc(U)*invbc(L)*b;

这里直接根据计算的，值得注意的是，Matlab中求矩阵逆的默认运算函数为inv()，但在高阶系数矩阵时，容易有L和U矩阵接近为奇异矩阵，计算机无法求逆，因此本文定义了invbc()函数进行求逆。

这里的invbc()函数参考了CSDN里的这篇文章

https://blog.csdn.net/weixin_42599354/article/details/129999786?spm=1001.2014.3001.5506

function [x,t]=chasing_method(A,b)
tic 
    n=length(b);
    L=zeros(n,n);
    U=diag(ones(n,1));
    L(1,1)=A(1,1);
    for k=2:1:n
        U(k-1,k)=A(k-1,k)/L(k-1,k-1);
        L(k,k)=A(k,k)-A(k,k-1)*U(k-1,k);
    end
    for j=2:1:n
        L(j,j-1)=A(j,j-1);
    end
    x=invbc(U)*invbc(L)*b;

t=toc
end
%%
%新函数，关于invbc
function invM = invbc(M)

    D = sqrt(diag(M));
    K = max(D)./D;
    K = diag(K);
    invM = K/(K*M*K)*K;    

return

5.Jacobi迭代法

Jacobi迭代法的主要迭代公式为

其中，对系数矩阵A分裂为A=D-L-U，D为A的对角元素，L为-A的除对角外的下三角元素，U为-A的除对角外的上三角元素。则进一步有

需要注意的是，与前文三个计算方法不同的是，迭代法还需要输入初值X0才能开始第一次迭代，因为这两种迭代方法不存在局部收敛与全局收敛的问题，可以任意取初值。本文取初始向量X0=(0，0，···，0)T。判别迭代终止的条件可以采取后验检验，即

e为可以停止运行的误差大小，本文取10-5，且取无穷范数。

此外，迭代法还需要考虑是否收敛的问题。由迭代法收敛的充要条件为

在每次迭代前，需要先编写程序判断该方程组能否用迭代方法解出，如不能则return函数。

function [X,i,eps,t]=jacobi_iteration(A,b,e,x1)
    
    D=diag(diag(A));%A的对角元素赋值给D
    U=-triu(A,1);%A的除对角外上三角元素赋值给U
    L=-tril(A,-1);%A的除对角外下三角元素赋值给L
    B=inv(D)*(L+U);
    eps=zeros(200,1);
    t=0;
    X=x1;
    i=0;
    if vrho(B)<1
        tic
        xx=1;%计算第k-1次和第k次迭代结果之间的误差
        i=0;
        while norm(xx,inf)>e
            eps(i+1,:)=norm(xx,inf);
            x=x1;
            x1=B*x+inv(D)*b;
            xx=x1-x;
            i=i+1;
            if norm(xx,inf)<=e
                X=x1;
                break
            end
        end
        t=toc
    else
        disp('警告：输入的系数矩阵使用Jacobi迭代法无法收敛！')
        return
    end
t=toc
end

6.Gauss-Seidel迭代法

Gauss seidel迭代法是对Jacobi迭代法的进一步优化，主要对每次迭代中最新计算出的第k+1次近似的分量加以利用，因此迭代公式改写为

其中

其他设置如迭代终止条件，判断迭代是否收敛等都与5节内容相同。

function [X,i,eps,t]=Guass_seidel_iteration(A,b,e,x1)
    
    D=diag(diag(A));
    U=-triu(A,1);
    L=-tril(A,-1);
    B=inv(D-L)*(U);
    eps=zeros(200,1);
    t=0;
    X=x1;
    i=0;
    if vrho(B)<1
        tic
        xx=1;%计算第k-1次和第k次迭代结果之间的误差
        i=0;
        while norm(xx,inf)>e
            eps(i+1,:)=norm(xx,inf);
            x=x1;
            x1=B*x+inv(D-L)*b;
            xx=x1-x;
            i=i+1;
            if norm(xx,inf)<=e
                X=x1;
                break
            end
            t=toc
        end
    else
        disp('警告：输入的系数矩阵使用Gauss_seidel迭代法无法收敛！')
        return
    end

end

7.主程序——调用函数解方程

这里直接调用各个函数就可以了，在已知精确解的前提下，可以利用范数计算出不同计算方法求得的解的误差。对于迭代方法可以比较迭代次数。此外，还可以比较各个计算方法程序运行的时间，这在解高阶矩阵时尤为重要。

clear;clc;close all
%这里A和b需要自己输入设定，此处略去


if cond(A)-1000>1
    disp('警告：输入的系数矩阵可能是病态矩阵！')
    disp('该系数矩阵的条件数为：')
    disp(cond(A))
    judge=input('继续运行请按回车');
end
err=zeros(5,1);
%顺序高斯消元法
[x_gauss,t_g]=gauss_elimination(A,b);
err(1)=norm(abs(x_gauss-x_ture),inf);
disp('顺序高斯消元法得到的方程组的解与精确解的误差为：')
disp(err(1))
%列主元高斯消元法
[x_lie,t_lie]=lie_gauss_elimination(A,b);
err(2)=norm(abs(x_lie-x_ture),inf);
disp('列主元高斯消元法得到的方程组的解与精确解的误差为：')
disp(err(2))
%追赶法
[x_chasing,t_chasing]=chasing_method(A,b);
err(3)=norm(abs(x_chasing-x_ture),inf);
disp('追赶法得到的方程组的解与精确解的误差为：')
disp(err(3))
%Jacobi迭代法
x0=zeros(n,1);
[x_ja,i_ja,eps_ja,t_ja]=jacobi_iteration(A,b,1e-5,x0);
er(4)=norm(abs(x_ja-x_ture),inf);
disp('Jacobi迭代法得到的方程组的解与精确解的误差为：')
disp(err(4))
%Gauss_seidel迭代法
[x_g_s,i_g_s,eps_g_s,t_g_s]=Guass_seidel_iteration(A,b,1e-5,x0);
err(5)=norm(abs(x_g_s-x_ture),inf);
disp('Gauss_seidel迭代法得到的方程组的解与精确解的误差为：')
disp(err(5))

%比较两种迭代法
subplot(2,1,1)
plot([1:1:i_ja],eps_ja(1:i_ja))
title('Jacobi迭代法')
xlabel('迭代次数')
ylabel('x^{k+1}-x^k')
subplot(2,1,2)
plot([1:1:i_g_s],eps_g_s(1:i_g_s))
title('Gauss seidel迭代法')
xlabel('迭代次数')
ylabel('x^{k+1}-x^k')

%计算各函数的运行时间
figure(2)
t=zeros(5,1);
t(1)=t_g;t(2)=t_lie;t(3)=t_chasing;t(4)=t_ja;t(5)=t_g_s;
plot([1:1:5],t)
xticks([1 2 3 4 5 ])
set(gca,'XTickLabel',{'顺序高斯消元法','列主元高斯消元法','追赶法','Jacobi迭代法','Gaus seidel迭代法'})
ylabel('程序运行时间')

%%
%比较各种求解方式得到的误差大小
[err_m,j]=max(err);
if j==1
    disp('误差最大的为顺序高斯消元法,误差为：')
    disp(err_m)
elseif j==2
    disp('误差最大的为列主元高斯消元法,误差为：')
    disp(err_m)
elseif j==3
    disp('误差最大的为追赶法,误差为：')
    disp(err_m)    
elseif j==4
    disp('误差最大的为Jacobi迭代法,误差为：')
    disp(err_m)      
elseif j==5
    disp('误差最大的为Gauss_seidel迭代法,误差为：')
    disp(err_m)     
end
        

8.结果展示

这里放出某方程的求解的运行时间比较。

对于两种迭代方法，也可以绘出迭代收敛图，进行进一步的比较分析。