【深度学习推荐系统（一）传统推荐模型的演化之协同过滤与逻辑回归】

前段时间看了王喆老师的《深度学习推荐系统》，在这里开个专题做一些重要知识点整理，相当于再看一遍这本书了。

传统推荐模型的演化关系图

 简要地讲传统推荐模 型的 发展脉络主要由以下几部分组成。

( 1 )协同过滤算法族 。 经典的协同过滤算法曾是推荐系统的首选模型，从物品相似度和用户相似度角度出发，协同过滤衍生出物品协同过滤( ltemCF) 和用户协同过滤 (UserCF) 两种算法 。 为了使协同过滤能够更好地处理稀疏共现矩阵问题 、 增强模型的泛化能力，从协同过滤衍生出矩阵分解模型( Matrix Factorization , MF) ，并发展出矩阵分解的各分支模型 。
( 2 )逻辑回归模型族 。 与协同过滤仅利用用户和物品之间的显式或隐式反馈信息相比，逻辑回归能够利用和融合更多用户、物品及上下文特征 。 从 LR 模型衍生出的模型同样"枝繁叶茂"，包括增强了非线性能力的大规模分片线性模型( Large Scale Piece-wise Linear Model , LS-PLM) ，由逻辑回归发展出来的 FM 模型，以及与多种不同模型配合使用后的组合模型，等等 。
( 3 )因子分解机模型族。因子分解机在传统逻辑回归的基础上，加入了 二 阶部分，使模型具备了进行特征组合的能力。更 进一步，在因子分解机基础上发展出来的域感知因子分解机( Field-aware Factorization Machi 时，FFM) 则通过加入特征域的概念，进一步加强了因子分解机特征交叉的能力 。
( 4 )组合模型 。为了融合多个模型的优点，将不同模型组合使用是构建推荐模型常用的方法。Facebook 提出的 GBDT+LR[梯度提升决策树( Gradient Boosting Decision Tree ) +逻辑回归 ] 组合模型是在业界影响力较大的组合方式 。 此外，组合模型中体现出的特征工程模型化的思想，也成了深度学习推荐模型的引子和核心思想之一 。

协同过滤与矩阵分解

协同过滤

协同过滤是一个非常直观 、 可解释性很强的模型，但它并不具备较强的泛化能力，换句话说，协同过滤无法将两个物品相似这 一 信息推广到其他物品的相似性计算上 。 这就导致了一个比较严重的问题一一热门的物品具有很强的头部效应，容易跟大量物品产生相似性;而尾部的物品由于特征向量稀疏，很少与其他物品产生相似性，导致很少被推荐。

举例来说，从某共现矩阵中抽出 A 、 B 、 C 、 D 四个物品的向量，利用余弦相似度计算出物品相似度矩阵。

 通过物品相似度矩阵可知， A 、 B 、 C 之间的相似度均为 0 ，而与 A 、 B 、 C最相似的物品均为物品 D ，因此在以 ltemCF 为基础构建的推荐系统中，物品 D将被推荐给所有对 A 、 B 、 C 有过正反馈的用户 。
但事实上，物品 D 与 A 、 B 、 C 相似的原因仅在于物品 D 是一件热门商品，系统无法找出 A 、 B 、 C 之间相似性的主要原因是其特征向 量 非常稀疏，缺乏相似性计算的直接数据 。 这一现象揭示了协同过滤的天然缺陷一一推荐结果的头部效应较明显，处理稀疏向量的能力弱。

为解决上述问题，同时增加模型的泛化能力，矩阵分解技术被提出 。 该方法在协同过滤共现矩阵的基础上，使用更稠密的隐向量表示用户和物品，挖掘用户和物品的隐含兴趣和隐含特征，在 一 定程度上弥补了协同过滤模型处理稀疏矩阵能力不足的问题 。
另外，协同过滤仅利用用户和物品的交互信息，无法有效地引人用户年龄、性别 、 商品描述 、 商品分类 、 当前时间等一系列用户特征 、 物品特征和上下文特征，这无疑造成了有效信息的遗漏 。 为了在推荐模型中引入这些特征，推荐系统逐渐发展到以逻辑回归模型为核心的 、 能够综合不同类型特征的机器学习模型的道路上。

矩阵分解

矩阵分解算法则期望为每一个用户和视频生成一个隐向量 ，将用户和视频定位到隐向量 的表示空间上(如图 2-4(b) 所示)，距离相近的用户和视频表明兴趣特点接近，在推荐过程中，就应该把距离相近的视频推荐给目标用户。

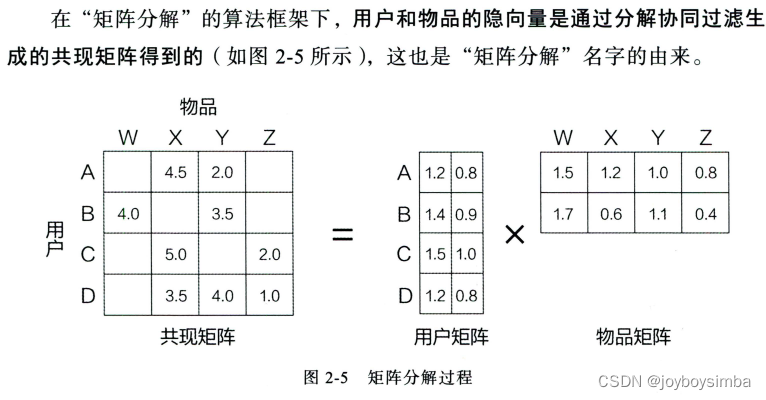
矩阵分解算法将 mxn 维的共现矩阵 R 分解为 m x k 维的用户矩阵 U 和 kxn维的物品矩阵 V 相乘的形式 。 其中 m 是用户数 量 ， n 是物品数 量 ， k 是隐向 量 的维度 。 k 的大小决定了隐向量表达能力的强弱 。 k 的取值越小，隐向 量 包含的信息越少，模型的泛化程度越高;反之 ，k 的取值越大，隐向 量 的表达能力越强，但泛化程度相应降低 。 此外 ， k 的取值还与矩阵分解的求解复杂度直接相关 。 在具体应用中 ，k的取值要经过多次试验找到一个推荐效果和工程开销的平衡点 。

矩阵分解两种方法：奇异值分解和梯度下降。

相比协同过滤，矩阵分解有如下非常明显的优点 。
( 1 )泛化能力强 。 在一定程度上解决了数据稀疏问题 。
( 2 )空间复杂度低 。 不需再存储协同过滤模型服务阶段所需的"庞大"的用户相似性或物品相似性矩阵，只需存储用户和物品隐向量 。 空间复杂度由 n2级别降低到 (n+m)×k 级别 。
( 3 )更好的扩展性和灵活性 。 矩阵分解的最终产出是用户和物品隐向量，这其实与深度学习中的 Embedding 思想不谋而合，因此矩阵分解的结果也非常便于与其他特征进行组合和拼接，并便于与深度学习网络进行无缝结合 。
与此同时，也要意识到矩阵分解的局限性 。

与协同过滤一样，矩阵分解同样不方便加入用户、物品和上下文相关的特征，这使得矩阵分解丧失了利用很多有效信息的机会，同时在缺乏用户历史行为时，无法进行有效的推荐 。 为了解决这个问题，逻辑回归模型及其后续发展出的因子分解机等模型，凭借其天然的融合不同特征的能力，逐渐在推荐系统领域得到更广泛的应用。

逻辑回归

逻辑回归模型常用的训练方法是梯度下降法 、 牛顿法 、 拟牛顿法等，其中梯度下降法是应用最广泛的训练方法，也是学习深度学习各种训练方法的基础。

逻辑回归模型的推断过程可以分为如下几步:
( 1 )将特征向量 x=(x1，x2，...， xn ) 作为模型的输入。
( 2 )通过为各特征赋予相应的权重(w1,w2, ..., wn+1 ) ，来表示各特征的重要性差异，将各特征进行加权求和，得到 xTw。
( 3 )将 xTw 输入 sigmoid 函数，使之映射到0-1的区间，得到最终的"点击率"。