数理逻辑
求前束范式的一般步骤:
- 利用等值公式消去“ → \rightarrow →”和“ ↔ \leftrightarrow ↔”
- 否定深入
- 改名
- 前移量词
仅含有全称量词的前束范式称为SKOLEM标准形。
SKOLEM标准形的求解算法:
- 先求谓词演算公式的前束范式
- 使用
n元函数干掉存在量词 - 从左至右重复上述过程,直至公式中不含有存在量词
量词消去/引入规则
- 全称量词消去规则
- 全称量词引入规则
- 存在量词消去规则
- 存在量词引入规则
集合论
空集是唯一的
幂集定义
A是一个集合,存在一个集合,它是由A的所有子集为元素构成的集合,称它为集合A的幂集合,记为P(A),也记为
2
A
2^A
2A。
P({Ø,{Ø}})={Ø,{Ø},{{Ø}}, {Ø,{Ø}}}
A是一个含有n个元素的集合,则幂集
2
A
2^A
2A 中A的子集总数为
2
n
2^n
2n。
集合的基本运算
- 并运算
- 交运算
- 相对补运算(差运算)
- 绝对补运算(补运算)
- 对称差
加法公式:
∣
A
1
∪
A
2
∣
=
∣
A
1
∣
+
∣
A
2
∣
−
∣
A
1
∩
A
2
∣
|A_1\cup A_2|=|A_1|+|A_2|-|A_1\cap A_2|
∣A1∪A2∣=∣A1∣+∣A2∣−∣A1∩A2∣
减法公式:
∣
A
−
B
∣
=
∣
A
∣
−
∣
A
∩
B
∣
|A-B|=|A|-|A\cap B|
∣A−B∣=∣A∣−∣A∩B∣
包含排斥原理(多退少补公式)
集合关系
设R是从A到B的一个二元关系,即
R
⊆
A
×
B
R\subseteq A\times B
R⊆A×B
若
R
=
∅
R=\varnothing
R=∅,称为空关系。
若
R
=
A
×
B
R=A\times B
R=A×B,称为全域关系。
当A=B时,将全域关系记作
E
A
E_A
EA,即
E
A
=
A
2
E_A=A^2
EA=A2
当A=B时,记
I
A
=
{
<
x
,
x
>
∣
x
∈
A
}
I_A=\{ <x,x>|x\in A \}
IA={<x,x>∣x∈A}称之为A上的恒等关系。
F
∘
G
=
{
<
x
,
y
>
∣
∃
z
(
<
x
,
z
>
∈
G
∧
<
z
,
y
>
∈
F
)
}
F\circ G=\{ <x,y>|\exist z(<x,z>\in G\wedge<z,y>\in F) \}
F∘G={<x,y>∣∃z(<x,z>∈G∧<z,y>∈F)}
显然,
F
∘
G
⊆
A
×
F
F\circ G\subseteq A\times F
F∘G⊆A×F,是一个从A到C的二元关系,称之为F与G的合成关系,也称为复合关系。
二元关系的表示方法
- 有序二元组
- 表
- 关系图
- 关系矩阵
域、限制、像
设A和B是两个集合,R是从A到B的一个二元关系,即
R
⊆
A
×
B
R\subseteq A\times B
R⊆A×B。令
d
o
m
R
=
{
x
∣
∃
y
(
<
x
,
y
>
∈
R
)
}
domR=\{ x| \exist y(<x,y>\in R) \}
domR={x∣∃y(<x,y>∈R)}
r
a
n
R
=
{
y
∣
∃
x
(
<
x
,
y
>
∈
R
)
}
ranR=\{ y|\exist x(<x,y>\in R) \}
ranR={y∣∃x(<x,y>∈R)}
f
l
d
R
=
d
o
m
R
∪
r
a
n
R
fldR=domR\cup ranR
fldR=domR∪ranR
分别称之为R的定义域、值域、域。
R
R
R在
A
′
A'
A′上的限制:
R
↾
A
′
=
{
<
x
,
y
>
∣
<
x
,
y
>
∈
F
∧
x
∈
A
′
}
R\upharpoonright A'=\{ <x,y>|<x,y>\in F\wedge x\in A' \}
R↾A′={<x,y>∣<x,y>∈F∧x∈A′}
R
R
R在
A
′
A'
A′上的像:
R
[
A
′
]
=
r
a
n
(
R
↾
A
′
)
R[A']=ran(R\upharpoonright A')
R[A′]=ran(R↾A′)
d
o
m
R
−
1
=
r
a
n
R
domR^{-1}=ranR
domR−1=ranR
r
a
n
R
−
1
=
d
o
m
R
ranR^{-1}=domR
ranR−1=domR
复合的逆等于逆的复合,但次序要交换
关系的性质
- 自反性
- 反自反性
- 对称性
- 反对称性
- 传递性
等价关系、等价类、商集
等价关系:自反、对称、传递
若R是非空集合A上的等价关系,x是A中任意一个元素,令
[
x
]
R
=
{
y
∣
x
∈
A
∧
<
x
,
y
>
∈
R
}
[x]_R=\{y |x\in A\wedge<x,y>\in R \}
[x]R={y∣x∈A∧<x,y>∈R}
[
x
]
R
[x]_R
[x]R为x关于R的等价类,简记为
[
x
]
[x]
[x]。是一个值的集合。
集合A关于等价关系R的商集:
A
/
R
=
{
[
X
]
R
∣
x
∈
A
}
A/R=\{ [X]_R|x\in A \}
A/R={[X]R∣x∈A}
x叫代表元
A={1,2,3}
R={<1,1>, <2,2>, <3,3>, <1,2>, <2,1>}

A
/
R
=
{
[
1
]
R
,
[
2
]
R
,
[
3
]
R
}
=
{
{
1
,
2
}
,
{
3
}
}
A/R=\{ [1]_R,[2]_R,[3]_R \}=\{ \{1,2\},\{3\} \}
A/R={[1]R,[2]R,[3]R}={{1,2},{3}}
集合的划分
若给定集合A上的一个划分π,可以在A上定义一个二元关系R,使得R成为A上的一个等价关系,且有:
A
/
R
=
π
A/R=\pi
A/R=π
偏序关系、偏序集
设A是一个非空集合,R是A上的一个二元关系,若R有自反性、反对称性、传递性,则称R是A上的一个偏序关系。并称(A,R)是一个偏序集。
一个偏序集,通常用符号
(
A
,
≤
)
(A,\leq)
(A,≤)来表示
一个偏序集
(
A
,
≤
)
(A,\leq)
(A,≤),包含集合A与集合A上的偏序关系
≤
\leq
≤。
- 不允许 x ∈ ( A , ≤ ) x\in(A,\leq) x∈(A,≤)出现
- 而仅有 x ∈ A x\in A x∈A,或 < x , y > ∈ ≤ <x,y>\in\leq <x,y>∈≤。
谈到元素是从A中取,讲到关系是在
≤
\leq
≤中取。
对于任意的
x
,
y
∈
A
x,y\in A
x,y∈A,若
x
≤
y
x\leq y
x≤y或者
y
≤
x
y\leq x
y≤x,则说x与y可比,否则说x与y不可比。
A={1,2,3,4}R={<1,1>,<2,2>,<3,3>,<4,4>,<1,2>,<1,3>,<1,4>,<2,4>}
R是A上一个偏序关系。3与4不可比。
覆盖、哈斯图(
Hasse Diagram)
设偏序集
(
A
,
≤
)
(A,\leq)
(A,≤),A是一个有限集,|A|=n。
如果不存在
z
∈
A
z\in A
z∈A,使得
x
≤
z
x\leq z
x≤z,且
z
≤
y
z\leq y
z≤y,那么称y覆盖x,或称y盖住x。
哈斯图:这个图形有n个顶点,每一个顶点表示A中一个元素,两个顶点x与y,若有y覆盖x,则点x在点y的下方,且两点之间有一条直线相连结。
设A={{1},{2},{3},{4},{1,2},{1,5},{3,6},{4,6},{0,3,6},{1,5,8},{0,3,4,6}}
R是A上的一个偏序关系:对于任意的
x
,
y
∈
A
x,y\in A
x,y∈A,
<
x
,
y
>
∈
R
<x,y>\in R
<x,y>∈R当且仅当
x
⊆
y
x\subseteq y
x⊆y。
如果A中的任意两个元素都是可比的,那么称
(
A
,
≤
)
(A,\leq)
(A,≤)为全序集,并称
≤
\leq
≤为
A
A
A上的全序关系。
一个有限的偏序集,一定有极大元和极小元,但不一定有最大元和最小元。

设a和b是A中的两个元素。如果A一个元素c满足
a
≤
c
a\leq c
a≤c且
b
≤
c
b\leq c
b≤c,说c是a和b的上界。
如果c是a和b的上界,并且若存在a和b的任意一个上界d,则有
c
≤
d
c\leq d
c≤d,称c为元素a和b的最小上界<least upper bound>,记为lub{a,b}=c。
如果A一个元素c满足
c
≤
a
c\leq a
c≤a且
c
≤
b
c\leq b
c≤b,说c是a和b的下界。
如果c是a和b的上界,并且若存在a和b的任意一个下界d,则有
d
≤
c
d\leq c
d≤c,称c为元素a和b的最大下界<greatest lower bound>,记为glb<a,b>=c。
若对于任意的元素a和b属于A,在A中存在a和b的最小上界及最大下界,则称
(
A
,
≤
)
(A,\leq)
(A,≤)是一个格。

函数
设A和B是两个非空集合,f是
A
×
B
A\times B
A×B的一个子集,即
f
⊆
A
×
B
f\subseteq A\times B
f⊆A×B。若对于任意的x∊A,存在唯一的
y
∈
B
y\in B
y∈B,使得
<
x
,
y
>
∈
f
<x,y>\in f
<x,y>∈f,则称f是从A到B的一个函数(映射)。
- d o m f = A domf=A domf=A
- r a n f ⊆ B ranf\subseteq B ranf⊆B
函数相等:
f
=
g
⇔
f
⊆
g
∧
g
⊆
f
f=g\Leftrightarrow f\subseteq g\wedge g\subseteq f
f=g⇔f⊆g∧g⊆f
B
A
B^A
BA读作“B上A”:所有从A到B的函数构成的集合。
B
A
=
{
f
∣
f
:
A
→
B
}
B^A=\{ f|f:A\rightarrow B \}
BA={f∣f:A→B}
如果
∣
A
∣
=
m
(
≠
0
)
|A|=m(≠0)
∣A∣=m(=0),
∣
B
∣
=
n
(
≠
0
)
|B|=n(≠0)
∣B∣=n(=0),则
∣
B
A
∣
=
n
m
|B^A|=n^m
∣BA∣=nm。
像、像源集
设
f
:
A
→
B
f:A\rightarrow B
f:A→B,
A
′
⊆
A
A'\subseteq A
A′⊆A,令
f
(
A
′
)
=
{
f
(
x
)
∣
x
∈
A
′
}
f(A')=\{ f(x)|x\in A' \}
f(A′)={f(x)∣x∈A′},称为
A
′
A'
A′在
f
f
f下的像。
当
A
′
=
A
A'=A
A′=A时,称
f
(
A
′
)
=
f
(
A
)
=
r
a
n
f
f(A')=f(A)=ranf
f(A′)=f(A)=ranf是函数的像(值域)

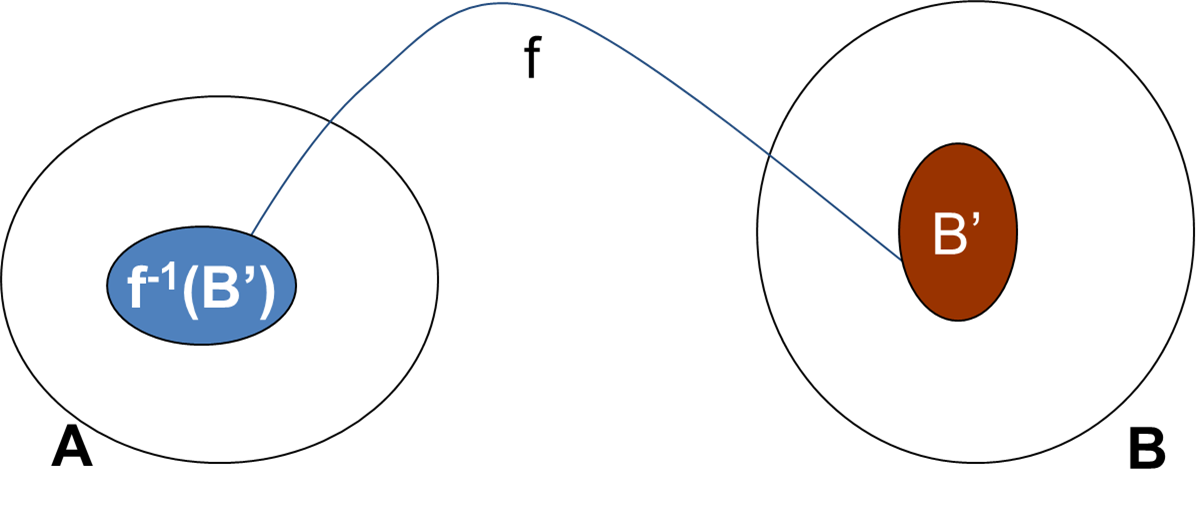
设
f
:
A
→
B
f:A\rightarrow B
f:A→B,
B
′
⊆
B
B'\subseteq B
B′⊆B,令
f
−
1
(
B
′
)
=
{
x
∈
A
∣
f
(
x
)
∈
B
′
}
⊆
A
f^{-1}(B')=\{ x\in A|f(x)\in B' \}\subseteq A
f−1(B′)={x∈A∣f(x)∈B′}⊆A称之为
B
′
B'
B′的像源集。
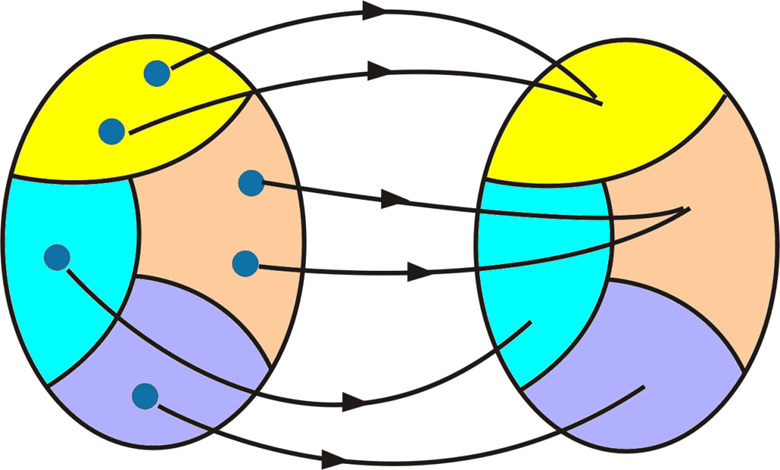
单射、满射、双射
f单射意味着:
f
(
x
1
)
=
f
(
x
2
)
⇒
x
1
=
x
2
f(x_1)=f(x_2)\Rightarrow x_1=x_2
f(x1)=f(x2)⇒x1=x2
若
r
a
n
f
=
f
(
A
)
=
B
ranf=f(A)=B
ranf=f(A)=B,则
f
:
A
→
B
f:A\rightarrow B
f:A→B是满射函数。
若f既是单射函数,又是满射函数,则称f是双射函数,也叫一一对应的函数。
常函数、恒等函数(恒等关系)、单调函数
常函数:值是个常数
恒等函数:
I
A
(
x
)
=
x
I_A(x)=x
IA(x)=x
单调函数
特征函数:有就是1,没有就是0
自然映射:
g
(
a
)
=
[
a
]
,
∀
a
∈
A
g(a) = [a],\forall a\in A
g(a)=[a],∀a∈A
设A,B是两个集合,若存在f:A→B,且f是双射函数,则称集合A与集合B的势相等,记为|A|=|B|
设A为可数无限集,记
∣
A
∣
=
ℵ
0
|A|=\aleph_0
∣A∣=ℵ0,读作“阿列夫零”
复合函数、反函数
函数的复合:二元关系的复合
反函数:不等于二元关系的逆,双射函数才有反函数

函数的逆关系不一定是个函数。
双射函数的逆关系是一个双射函数。
图
无序积、多重集
无序积中的元素是两个元素的集合{a,b},其中a与b不分次序。不宜将{a,b}记作为(a,b),一般认为(a,b)=<a,b>中a与b是有次序的。
- A & B = { { x , y } ∣ x ∈ A ∧ y ∈ B } A\&B=\{\{x,y\}|x\in A\wedge y\in B\} A&B={{x,y}∣x∈A∧y∈B}
约定一个多重集是一些对象的总体,但这些对象不必不同。一个元素的重数是它在该多重集里出现的次数。集合仅是多重集中重数仅为0和1的特殊情况
{a,a,a,b,b,c}
无向图、有向图
设V是一个非空有限集合,E是无序积V&V的一个多重子集,则称二元组G=(V,E)是一个无向图。

设V是一个非空有限集合,E是笛卡尔积V×V的一个多重子集,则称二元组G=(V,E)是一个无向图。

多重图、简单图
通常用G表示无向图,D表示有向图,也常用G泛指无向图和有向图。
V(G),E(G),V(D),E(D):G和D的顶点集, 边集
**n**阶图:n个顶点的图
零图:
E
=
∅
E=\varnothing
E=∅
平凡图:1阶零图
空图:
V
=
∅
V=\varnothing
V=∅
端点、相邻、关联次数、孤立点、环
在无向图中,如果有2条或2条以上的边关联同一对顶点,则称这些边为平行边,平行边的条数称为重数。
在有向图中,如果有2条或2条以上的边具有相同的始点和终点,则称这些边为有向平行边,简称平行边,平行边的条数称为重数。
含平行边的图称为多重图。
既无平行边也无环的图称为简单图。
度、握手定理
点的入度、出度、度
图的最大出度、最小出度、最大入度、最小入度、最大度、最小度
悬挂顶点、悬挂边
握手定理:
Σ
d
(
v
)
=
2
∣
E
∣
\Sigma d(v)=2|E|
Σd(v)=2∣E∣
在一个图中,度数为奇数的顶点必有偶数个。
顶点度序列:顶点度序列是一组正整数,每一个数对应某一个顶点的度数。

完全图
n阶无向完全图:每个顶点都与其余顶点相邻的n阶无向简单图
n阶有向完全图:每对顶点之间均有两条方向相反的有向边的n阶有向简单图
子图、母图、生成子图、真子图、导出子图
补图
无向图的同构
任意两个同构的无向图,一定有一个同样的顶点度序列。
一个无向简单图如果同构于它的补图,则称这个图为自互补图。

通路、回路、图的连通性
通路:顶点序列、边序列、顶点与边的交替序列。
称一条通路经过的边的多少为这条通路的长度。
称两个顶点间的最短通路的长度为该两个顶点间的距离。
称一条通路为简单通路,如果它的每一条边都不重复出现。
称一条通路为初等通路,如果它的每一个顶点都不重复出现。

若一个回路中边不重复出现,则称之为简单回路。
若一个回路中顶点不重复出现,则称之为初等回路,又称之为圈。

环是长度为1的圈;
两条平行边构成长度为2的圈;
在无向简单图中, 所有圈的长度
≥
3
\geq3
≥3
在有向简单图中, 所有圈的长度
≥
2
\geq2
≥2
在n阶图G中,若从顶点u到v
(
u
≠
v
)
(u\neq v)
(u=v)存在通路,则从u到v存在长度小于等于
n
−
1
n-1
n−1的初级通路
在n阶图G中,若存在v到自身的简单回路,则存在v到自身长度小于等于n的初级回路
连通:无向图中有通路
可达:有向图中有通路
连通是等价关系(规定u与自身总连通)
可达具有自反性和传递性(规定u到自身总是可达的)
连通图
连通分支、连通分支数
强连通
⇒
\Rightarrow
⇒单向连通
⇒
\Rightarrow
⇒弱连通
强连通与单向连通图判别法:
D强连通当且仅当D中存在经过每个顶点至少一次的回路。D单向连通当且仅当D中存在经过每个顶点至少一次的通路。

点割集(割点),点连通度
如果全部擦除
V
′
V'
V′中的顶点以及相应的边,所剩下的图的连通分支个数增加,并且部分擦除
V
′
V'
V′中的顶点以及相应的边,所剩下的图的连通分支个数不变。
当点割集
V
′
V'
V′为单点集
{
v
1
}
\{ v_1 \}
{v1}时,称该顶点
v
1
v_1
v1为割点。
称点割集中最小顶点数
m
i
n
∣
V
′
∣
min|V'|
min∣V′∣为点连通度。

边割集 (割边/桥),边连通度
如果全部擦除
E
′
E'
E′中的边,所剩下的图的连通分支个数增加,并且部分擦除
E
′
E'
E′中的边,所剩下的图的连通分支个数不变。
当割边集
E
′
E'
E′为单点集
{
e
1
}
\{ e_1 \}
{e1}时,称该边
e
1
e_1
e1为割边,或桥。
称边割集中的最小边数
m
i
n
∣
E
′
∣
min|E'|
min∣E′∣为边连通度。
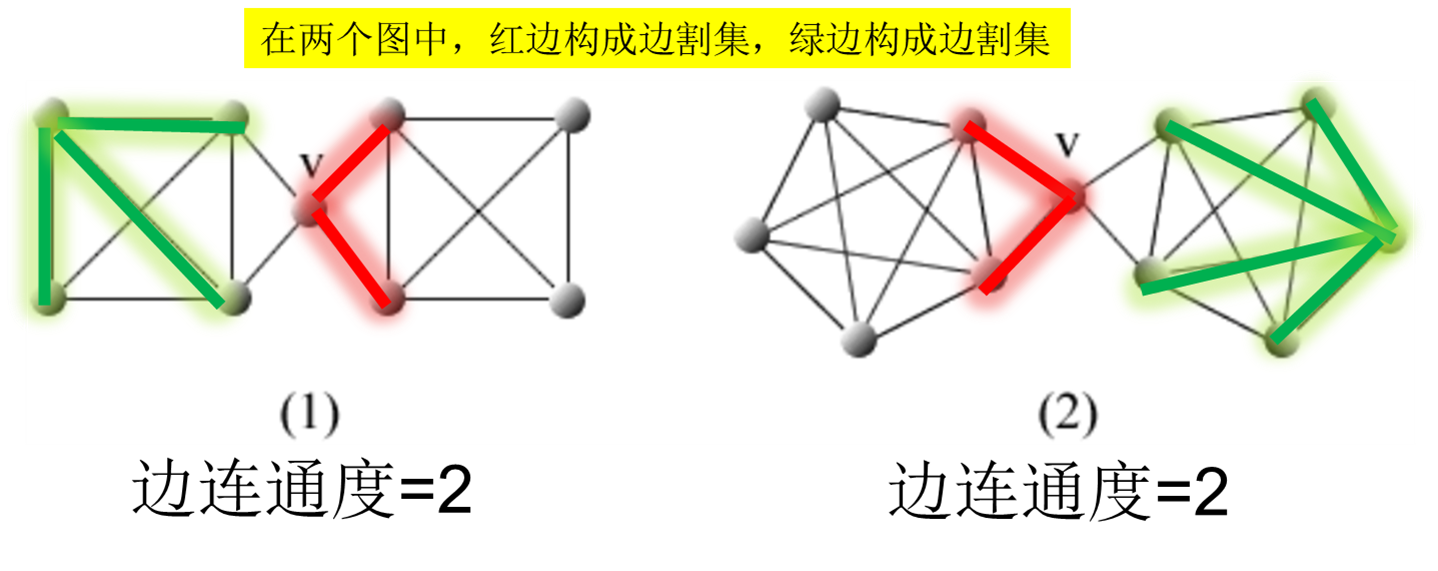
点连通度 ≤ \leq ≤边连通度 ≤ \leq ≤顶点最小度

无向图的关联矩阵


























 2137
2137

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










