二元逻辑回归损失函数的数学解释与公式推导

我们基于极大似然法来推导二元逻辑回归的损失函数，这个推导过程能够帮助我们了解损失函数怎么
得来的，以及为什么$J(\theta )$的最小化能够实现模型在训练集上的拟合最好。

我们的目标是：让模型对训练数据的效果好，追求损失最小

二元逻辑回归的标签服从伯努利分布(即0-1分布)，因此我们可以将一个特征向量为 $x$，参数为$\theta$的模型中的一个样本i的预测情况表现为如下形式：

• 样本i在由特征向量 $x_i$和参数 $\theta$组成的预测函数中，样本标签被预测为1的概率为：

  $$P_1=P(\widehat{y_i}=1|x_i,\theta )=y_{\theta }(x_i)$$

• 样本i在由特征向量 和参数 组成的预测函数中，样本标签被预测为0的概率为：

  $$P_0=P(\widehat{y_i}=0|x_i,\theta )=1-y_{\theta }(x_i)$$

当$P_1$的值为1的时候，代表样本i的标签被预测为1，当$P_0$的值为1的时候，代表样本i的标签被预测为0。

假设样本i的真实标签$y_i$为1，此时如果$P_1$为1，$P_0$为0的时候，就代表样本i的标签被预测为1，与真实值一致。此时对于单样本i来说，模型的预测就是完全准确的，拟合程度很优秀，没有任何信息损失。

相反，如果$P_1$为0，$P_0$为1的时候，就代表样本i的标签被预测为0，与真实情况完全相反。对于单样本i来说，模型的预测就是完全错误的，拟合程度很差，所有的信息都损失了。

当$y_i$为0时，也是同样的道理，所以，当 $y_i$为1的时候，我们希望 $P_1$非常接近1， 当 $y_i$为0的时候，我们希望 $P_0$非常接近1，这样，模型的效果就很好，信息损失就很少。

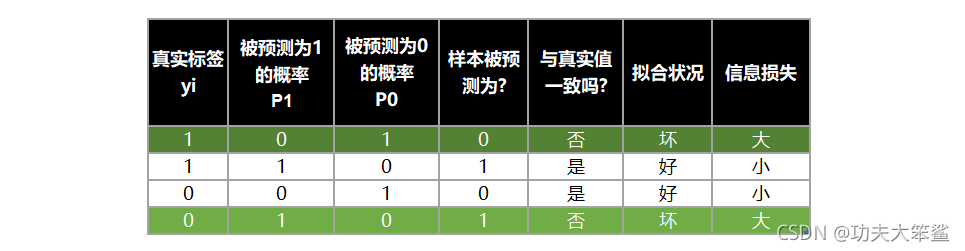
将两种取值的概率整合，我们可以定义如下等式：
$$P(\widehat{y_i}|x_i,\theta )=P_1^{y_i}\ast P_0^{1-y_i}$$

这个等式代表同时代表了$P_0$和$P_1$，当样本i的真实标签 $y_i$为1的时候，$1-y_i$ 就等于0，$P_0$ 的0次方就是1，所以$P(\widehat{y_i}|x_i,\theta )$等于$P_1$，这时，如果$P_1$为1，模型的效果就很好，损失就很小。同理，当 $y_i$为0的时候，$P(\widehat{y_i}|x_i,\theta )$等于$P_0$，此时如果$P_0$非常接近1，模型的效果就很好，损失就很小。所以，为了达成让模型拟合好，损失小的目的，我们每时每刻都希望$P(\widehat{y_i}|x_i,\theta )$ 的值等于1。 而$P(\widehat{y_i}|x_i,\theta )$ 的本质是样本i由特征向量$x_i$和参数$\theta$组成的预测函数中，预测出所有可能的$\hat{y}$的概率，因此1是它的最大值。

也就是说，每时每刻，我们都在追求$P(\widehat{y_i}|x_i,\theta )$ 的最大值。这就将模型拟合中的“最小化损失”问题，转换成了对函数求解极值的问题。

$P(\widehat{y_i}|x_i,\theta )$是对单个样本i而言的函数，对一个训练集的m个样本来说，我们可以定义如下等式来表达所有样本在特征矩阵X和参数 $\theta$组成的预测函数中，预测出所有可能的 $\hat{y}$的概率P为：
$$\begin{array}{rl}P& =\prod _{i=1}^{m}P(\widehat{y_i}|x_i,\theta )\\ & =\prod _{i=1}^m(P_1^{y_i}\ast P_0^{1-y_i})\\ & =\prod _{i=1}^m(y_0(x_i{)}^{y_i}\ast (1-y_0(x_i){)}^{1-y_i})将开头的P_1和P_0带入\end{array}$$

对该概率P取对数，再由$\log (A\ast B)=\log A+\log B$和$\log A^B=B\log A$可得：
$$\begin{array}{rl}\log P& =\log \prod _{i=1}^m(y_0(x_i{)}^{y_i}\ast (1-y_0(x_i){)}^{1-y_i})\\ & =\sum _{i=1}^m\log (y_0(x_i{)}^{y_i}\ast (1-y_0(x_i){)}^{1-y_i})\\ & =\sum _{i=1}^m(\log y_{\theta }(x_i{)}^{y_i}+\log (1-y_{\theta }(x_i){)}^{1-y_i})\\ & =\sum _{i=1}^m(y_i\log y_{\theta }(x_i)+(1-y_i)\log (1-y_{\theta }(x_i)))\end{array}$$

这就是我们的交叉熵函数。为了数学上的便利以及更好地定义”损失”的含义，我们希望将极大值问题转换为极小值问题，因此我们对 $\log P$取负，并且让参数 $\theta$作为函数的自变量，就得到了我们的损失函数 $J(\theta )$：
$$J(\theta )=-\sum _{i=1}^m(y_i\log y_{\theta }(x_i)+(1-y_i)\log (1-y_{\theta }(x_i)))$$

这就是一个，基于逻辑回归的返回值 $y_{\theta }(x_i)$的概率性质得出的损失函数。在这个函数上，我们只要追求最小值，就能让模型在训练数据上的拟合效果最好，损失最低。这个推导过程，其实就是“极大似然法”的推导过程。

似然与概率

• 似然与概率是一组非常相似的概念，它们都代表着某件事发生的可能性，但它们在统计学和机器学习中有着微妙的不同。以样本i为例，表达式为：
  $$P(\widehat{y_i}|x_i,\theta )$$
  对这个表达式而言，如果参数 $\theta$是已知的，特征向量$x_i$是未知的，我们便称P是在探索不同特征取值下获取所有可能的 $\hat{y}$的可能性,这种可能性就被称为概率，研究的是自变量和因变量之间的关系。

  如果特征向量$x_i$ 是已知的，参数$\theta$ 是未知的，我们便称P是在探索不同参数下获取所有可能的 $\hat{y}$ 的可能性，这种可能性就被称为似然，研究的是参数取值与因变量之间的关系。

  在逻辑回归的建模过程中，我们的特征矩阵是已知的，参数是未知的，因此我们讨论的所有“概率”其实严格来说都应该是“似然”。我们追求$P(\widehat{y_i}|x_i,\theta )$ 的最大值（换算成损失函数之后取负了，所以是最小值），就是在追求“极大似然”，所以逻辑回归的损失函数的推导方法叫做”极大似然法“。也因此，以下式子又被称为”极大似然函数“：
  $$P(\widehat{y_i}|x_i,\theta )=y_0(x_i{)}^{y_i}\ast (1-y_0(x_i){)}^{1-y_i}$$