数学建模——图与网络模型及方法（二）

目录

基本概念

求取最小生成树

着色问题

最大流问题

最小费用流问题

旅行商问题

---

基本概念

连通的无圈图称为树。例如：

 生成树：若图G的生成子图H是树，则称H为G的生成树或支撑树。边权之和最小的生成树是最小生成树。连通图的生成树一定存在。

构造连通图最小生成树的算法有Kruskal算法和Prim算法。

求取最小生成树

Kruskal、Prim算法

例如，求取如下最小生成树：

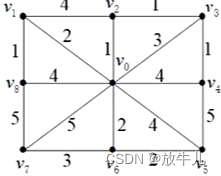
clc,clear,close all,a=zeros(9);
a(1,[2:9])=[2 1 3 4 4 2 5 4];
a(2,[3,9])=[4,1];a(3,4)=1;a(4,5)=1;
a(5,9)=5;a(6,7)=2;a(7,8)=3;a(8,9)=5;
s=cellstr(strcat('v',int2str([0:8]')));
G=graph(a,s,'upper');p=plot(G,"EdgeLabel",G.Edges.Weight);
T=minspantree(G,'Method','sparse');%sparse为Kruskal算法，dense为Prim算法
L=sum(T.Edges.Weight);
highlight(p,T);

数学规划模型

 约束条件：

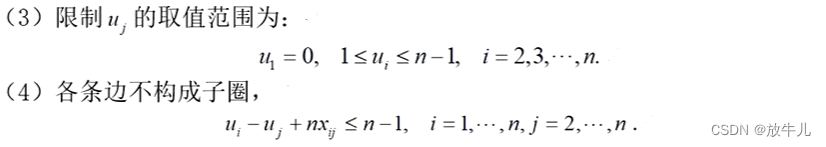
 上方的例子进行求解：

clc,clear,close all,n=9;
nod = cellstr(strcat('v',int2str([0:n-1]')));
G = graph;G = addnode(G,nod);%将新节点添加到图
ed = {'v0','v1',2;'v0','v2',1;'v0','v3',3;'v0','v4',4;
      'v0','v5',4;'v0','v6',2;'v0','v7',5;'v0','v8',4;
      'v1','v2',4;'v1','v8',1;'v2','v3',1;'v3','v4',1;
      'v4','v5',5;'v5','v6',2;'v6','v7',4;'v7','v8',5};
G = addedge(G,ed(:,1),ed(:,2),cell2mat(ed(:,3)));
w = full(adjacency(G,'weighted'));
w(w==0) = 1000000%表示充分大的正实数
prob = optimproblem;
x = optimvar('x',n,n,'Type','integer','LowerBound',0,'UpperBound',1);
u = optimvar('u',n,'LowerBound',0);
prob.Objective = sum(sum(w.*x));
prob.Constraints.con1 = [sum(x(:,[2:end]))'==1;u(1)==0];
con2 = [1<=sum(x(1,:));1<=u(2:end);u(2:end)<=n-1];
for i = 1:n
    for j = 2:n
        con2 = [con2;u(i)-u(j)+n*x(i,j)<=n-1];
    end
end
prob.Constraints.con2 = con2;
[s,f,flag,out] = solve(prob);
[i,j]=find(s.x);
ind = [(i-1)';(j-1)']

着色问题

顶点着色问题：已知图G=(V,E)，对图G的所有顶点进行着色时，要求相邻的两顶点的颜色不一样，至少需要几种颜色。

边着色问题：对图G的所有边进行着色时，要求相邻的两条边的颜色不一样，至少需要几种颜色。

 在图论中，一个点的度（degree）指图中与该点相连的边数。

例子：

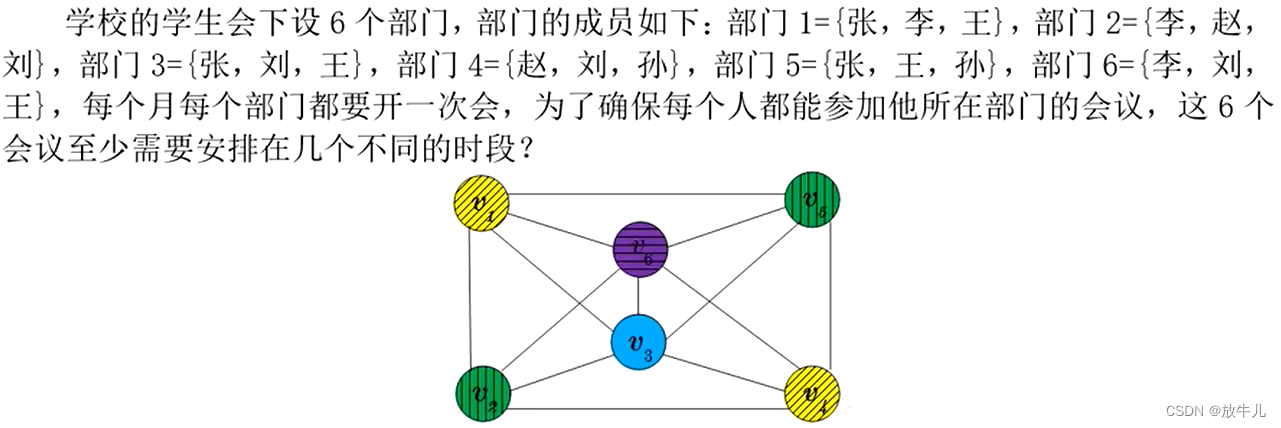
将部门看做点，部门有重复成员的就相连。根据定理有

 条件限定依次是：每一个顶点只能有一种颜色，相连的两个顶点颜色不能一样，得知颜色数目，x只能为0或者1。

clc,clear
s = {{'张','李','王'};{'赵','李','刘'};{'张','刘','王'};
     {'赵','刘','孙'};{'张','孙','王'};{'刘','李','王'}};
n = length(s);w = zeros(n);
for i = 1:n-1
    for j = i+1:n
        if ~isempty(intersect(s{i},s{j}))
            w(i,j) = 1;%如果有交集，则两个点有连线
        end
    end
end
[ni,nj] = find(w);
w = w+w';
deg = sum(w);K = max(deg)%寻找顶点的最大度，定理要用
prob = optimproblem;
x = optimvar('x',n,K+1,'Type','integer','LowerBound',0,'UpperBound',1);
y = optimvar('y');
prob.Objective = y;
prob.Constraints.con1 = sum(x,2)==1;
prob.Constraints.con2 = x(ni,:)+x(nj,:)<=1;
prob.Constraints.con3 = x*[1:K+1]'<=y;
[s,fval,flag,o] = solve(prob)
[i,k] = find(s.x);
ik = [i';k']

最大流问题

最大流问题就是使得网络中流量最大的问题。

可行流满足条件：

 c为每一条线上的容量，v就是总共的流量，A是所有线的集合

可以写成线性规划模型：

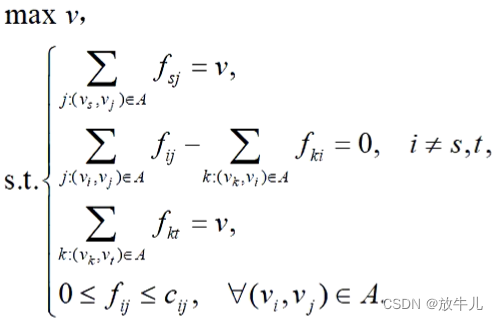
 例子（用matlab自带函数）：

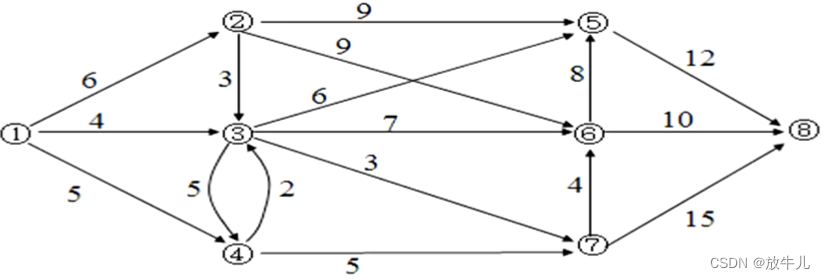
 求①到⑧的最大流：

clc,clear
a = zeros(8);
a(1,[2:4])=[6,4,5];a(2,[3,5,6])=[3,9,9];
a(3,[4:7])=[5,6,7,3];a(4,[3,7])=[2,5];
a(5,8)=12;a(6,[5,8])=[8,10];
a(7,[6,8])=[4,15];
G=digraph(a);H=plot(G,'EdgeLabel',G.Edges.Weight);
[M,F]=maxflow(G,1,8);
F.Edges
highlight(H,F);

也可以用规划的方法求取最大流。

最小费用流问题

在完成运输的同时，寻求运输费最小的运输方案。

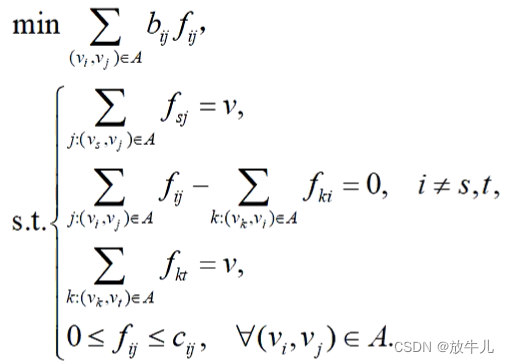
如果v大于最大流，则问题无解。 

例子：

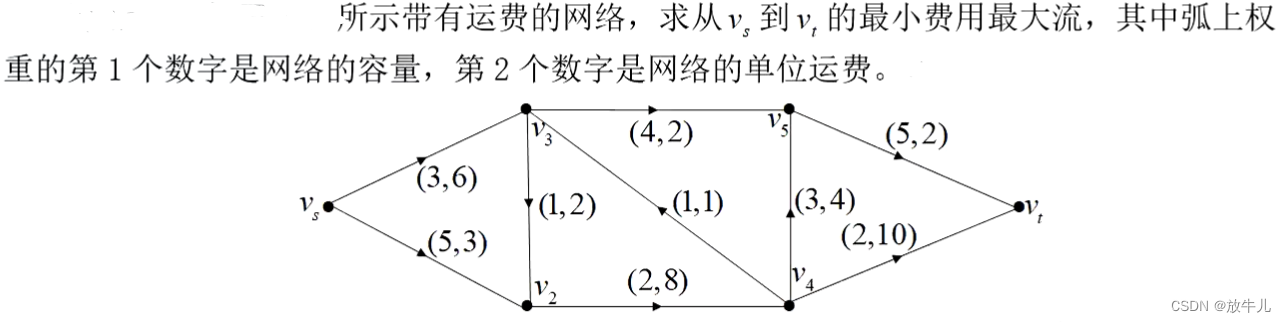
clc,clear
%% 先求出最大流
NN = cellstr(strcat('v',int2str([2:5]')));
NN = {'vs',NN{:},'vt'};%转换后是1*6的数组
L  = {'vs','v2',5,3;'vs','v3',3,6;
    'v2','v4',2,8;'v3','v2',1,2;
    'v3','v5',4,2;'v4','v3',1,1;
    'v4','v5',3,4;'v4','vt',2,10;
    'v5','vt',5,2};
G  = digraph;
G  = addnode(G,NN);
G1 = addedge(G,L(:,1),L(:,2),cell2mat(L(:,3)));
[M,F] = maxflow(G1,'vs','vt')

H=plot(G1,'EdgeLabel',G1.Edges.Weight);
highlight(H,F);
%% 求最小费用
G2 = addedge(G,L(:,1),L(:,2),cell2mat(L(:,4)));
c  = full(adjacency(G1,"weighted"));%导出流量矩阵
b  = full(adjacency(G2,"weighted"));%导出费用矩阵
f  = optimvar('f',6,6,'LowerBound',0);
prob = optimproblem;
prob.Objective = sum(b.*f,"all");
con1 = [sum(f(1,:))==M
        sum(f(:,[2:end-1]))'==sum(f([2:end-1],:),2)
        sum(f(:,end))==M];
prob.Constraints.con1 = con1;
prob.Constraints.con2 = f<=c;
[s,fval,flag,out] = solve(prob)
ff = s.f

旅行商问题

使用规划模型：

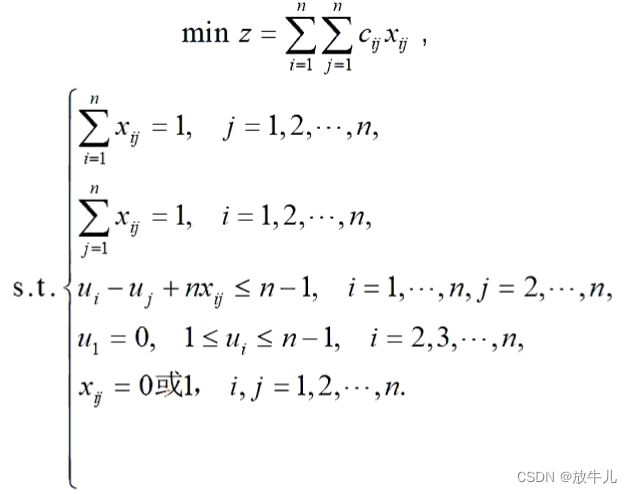
 例子：

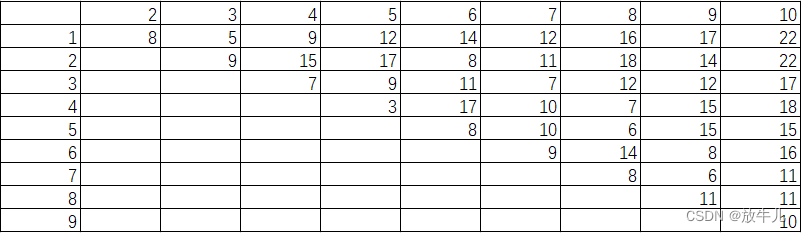
clc,clear
a = readmatrix('data.xlsx');
a(isnan(a)) = 0;n = 10;
b = zeros(n);
b([1:end-1],[2:end]) = a;
b = b+b';
b([1:n+1:end]) = 1000000;
prob = optimproblem;
x = optimvar('x',n,n,'Type','integer','LowerBound',0,'UpperBound',1);
u = optimvar('u',n,'LowerBound',0);
prob.Objective = sum(b.*x,"all");
prob.Constraints.con1 = [sum(x,2)==1;sum(x,1)'==1;u(1)==0];
con2 = [1<=u(2:end);u(2:end)<=14];
for i = 1:n
    for j = 2:n
        con2 = [con2;u(i)-u(j)+n*x(i,j)<=n-1];
    end
end
prob.Constraints.con2 = con2;
[s,fval,flag] = solve(prob)
xx = s.x;[i,j] = find(xx);
ij = [i';j']

结果为：

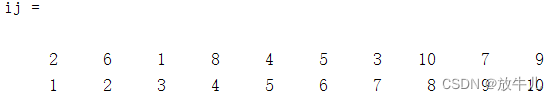
 最优路径为1 3 7 9 10 8 4 5 6 2 1。