数学建模——图与网络模型及方法（一）

放牛儿

已于 2022-07-06 16:31:09 修改

阅读量2.2k

点赞数 3

分类专栏：数学建模文章标签：算法

于 2022-06-25 17:57:39 首次发布

本文链接：https://blog.csdn.net/m0_51311105/article/details/125444577

版权

数学建模专栏收录该内容

10 篇文章

订阅专栏

本文介绍了MATLAB在图论中的应用，包括使用邻接矩阵和关联矩阵表示图，以及如何通过Dijkstra算法和Floyd算法求解最短路径问题。此外，还探讨了0-1整数规划方法在寻找最短路径中的应用，提供了一系列MATLAB代码示例来解决实际问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

基本概念

图，就是由一些点和这些点之间的连线组成。

|V|表示图G中顶点的个数，|E|表示边的条数。每一条边都是由连接G中两个顶点得到的一条线，记作： $c_{k}=(v_{i},v_{j})$ ，vi和vj称为边 $c_{k}$ 的两个端点。无向图中， $(v_{i},v_{j})$ 和 $(v_{j},v_{i})$ 表示的是同一条边 $c_{k}$ 。有公共顶点的两条边称为相邻的边，或称为邻边。同一条边的两个顶点称为相邻的顶点。带有方向的边称为有向边，又称为弧。如果给无向边的每条边规定一个方向，就得到了有向图。

赋权图：图的每条边都附有一个实数，实数称为权。记作 $G=(V,E,W)$ 。

图的矩阵表示

关联矩阵：（不同软件定义可能不一样）

邻接矩阵：

例如：

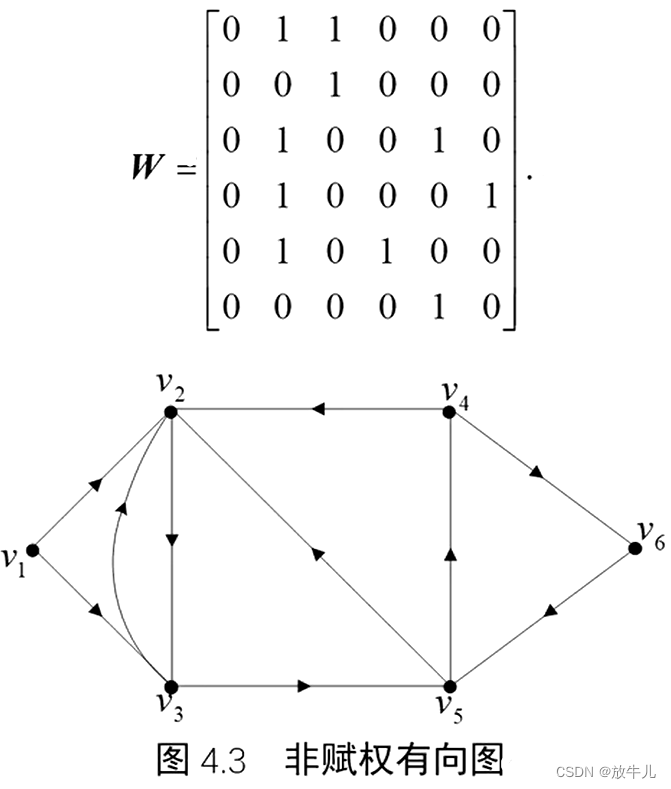
MATLAB工具箱使用

图的生成：

S = sparse(A)
%将矩阵A转化为稀疏矩阵形式，即矩阵A中任何0元素被去除，⾮零元素及其下标组成矩阵S。如果A本⾝是稀疏的，sparse(S)返回S。

A=full(S)

%把稀疏矩阵S转换为全矩阵存储形式A

MATLAB中一般使用稀疏矩阵来生成邻接矩阵

例如：画出下图非赋权有向图并导出邻接矩阵和关联矩阵

clc,clear,close all
E = [1,2;1,3;2,3;3,2;3,5;4,2;4,6;5,2;5,4;6,5];
s = E(:,1);
t = E(:,2);
nodes = cellstr(strcat('v',int2str([1:6]')))
%cellstr用于转换为字符向量元胞数组
%strcat用于水平串联字符串
G = digraph(s,t,[],nodes);
plot(G,'LineWidth',1.5,'Layout','circle','NodeFontSize',15)
%layout参数可以查阅帮助文档
W1 = adjacency(G)%用于导出邻接矩阵的稀疏矩阵
W2 = incidence(G)%用于导出关联矩阵的稀疏矩阵，使用full函数即可还原

最短路径算法

管道铺设、线路安排、厂区布局、设备更新等都可以归结为最短路径来解决

定义：

若两个顶点的路径不止一条，则最短路的长称为二点 $u_{0},v_{0}$ 的距离，记作 $d(u_{0},v_{0})$

计算最短路的算法有迪克斯特拉标号算法和弗洛伊德算法，前者只适用于边权是非负的情况。最短路问题也可以归结为一个0-1整数规化模型。

固定起点的最短路（Dijkstra算法）

寻求从一固定点到其余各点的最短路，Dijkstra算法就很有效，它是一种迭代算法。

MATLAB工具箱中，如果两个顶点之间没有边，对应的邻接矩阵元素为0，而不是像数学理论上对应无穷或0。

例子

线侧数字为所需费用，求从1到8费用最小的旅行路线。

clc,clear,close all
E = [1,2,6;1,3,3;1,4,1;2,5,1;3,2,2;
    3,4,2;4,6,10;5,4,6;5,6,4;5,7,3;
    5,8,6;6,5,10;6,7,2;7,8,4;9,5,2;9,8,3];
G = digraph(E(:,1),E(:,2),E(:,3));%起点，终点，权重
plot(G);
[path,d] = shortestpath(G,1,8,"Method","positive")%1,8代表源和终止节点，method可以看帮助文档，positive代表的是Dijkstra算法

可以通过上面这个使得图中的path点变得更大。

对于赋权无向图，将上面的代码使用graph函数就行，另一种(求1到11)：

clc,clear,close all
a=zeros(11);
a(1,2)=2;a(1,3)=8;a(1,4)=1;
a(2,3)=6;a(2,5)=1;
a(3,4)=7;a(3,5)=5;a(3,6)=1;a(3,7)=2;
a(4,7)=9;a(5,6)=3;a(5,8)=2;a(5,9)=9;
a(6,7)=4;a(6,9)=6;a(7,9)=3;a(7,10)=1;
a(8,9)=7;a(8,11)=9;
a(9,10)=1;a(9,11)=2;a(10,11)=4;
s=cellstr(strcat('v',int2str([1:11]')));
G=graph(a,s,'upper');
[p,d]=shortestpath(G,1,11);
h=plot(G,'EdgeLabel',G.Edges.Weight);%将权重显示在图上
highlight(h,p,'EdgeColor','red','LineWidth',2);%将通路高亮显示

%% [p,d,ed]=shortestpath(G,1,11);
%% highlight(h,"Edges",ed)

所有顶点对之间的最短路Floyd算法

采用Floyd算法，该算法允许赋权图中包含负权的边或弧，但是，每一个回路上的所有弧总和为非负。

计算时用迭代公式：

k为迭代次数，当k=n时，得到各顶点之间的最短距离值。

例子

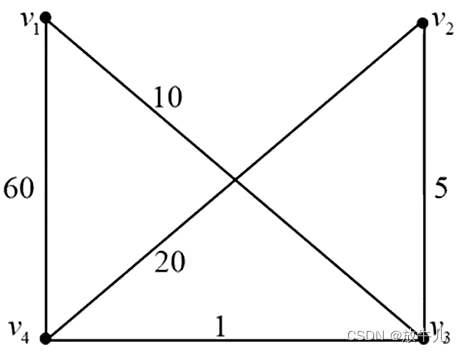
求得所有顶点之间的最短距离矩阵：

clc,clear,close all
a=zeros(4);
a(1,[3,4])=[10,60];
a(2,[3,4])=[5,20];
a(3,4)=1;
n=length(a);
b=a+a';
b(b==0)=inf;%
b([1:5:end])=0;%将其转换为标准的邻接矩阵
path=zeros(4);
for k=1:n
    for i=1:n
        for j=1:n
            if b(i,j)>b(i,k)+b(k,j)%b(i,j)表示从i到j
                b(i,j)=b(i,k)+b(k,j);
                path(i,j)=k;
            end
        end
    end
end
b,path

直接调用Dijkstra算法可以求各个顶点之间的最短距离:

clc,clear,close all
a=zeros(4);
a(1,[3,4])=[10,60];%定义相邻的点即可
a(2,[3,4])=[5,20];
a(3,4)=1;
G=graph(a,'upper');
d=distances(G,'Method','positive')

0-1整数规划方法

例子

求2到4的最短路径和最短距离（第一个条件i是不包括起始、终止点）

clc,clear,close all
a=zeros(6);
a(1,[2,5])=[18,15];
a(2,[3,4,5])=[20,60,12];
a(3,[4,5])=[30,18];
a(4,6)=10;
a(5,6)=15;
b=a+a';
b(b==0)=1000000%充分大的正实数即可
x=optimvar('x',6,6,'Type','integer','LowerBound',0,'UpperBound',1);
p=optimproblem("Objective",sum(b.*x,"all"));
con=[sum(x(2,:))==1;
    sum(x(:,2))==0;
    sum(x(:,4))==1];
for i = [1,3,5,6]%不包括起始、终止点
    con=[con;sum(x(i,:))==sum(x(:,i))];
end
p.Constraints=con;
[s,f]=solve(p),xx=s.x
[i,j]=find(xx);
ij=[i';j']