数学建模——线性规划

最新推荐文章于 2025-02-27 18:08:45 发布

放牛儿

最新推荐文章于 2025-02-27 18:08:45 发布

阅读量1.7w

点赞数 46

分类专栏：数学建模文章标签：动态规划算法

本文链接：https://blog.csdn.net/m0_51311105/article/details/125351884

版权

数学建模专栏收录该内容

10 篇文章

订阅专栏

基本概念

运筹学的一个重要分支是数学规划，线性规划是数学规划的一个重要的分支。

变量称为决策变量，规划的目标称为目标函数，限制条件称为约束条件，s.t.是“受约束于”的意思。

建立线性规划模型的一般步骤为：①分析问题，找出决策变量。②找出等式或不等式约束条件。③构造关于决策变量的一个线性函数。

线性规划模型的一般形式：

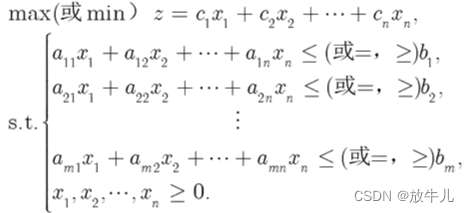
或：

$c=[c_{1},c_{2},...,c_{n}]^{T}$ 为目标函数的系数向量，又称为价值向量； $x=[x_{1},x_{2},...,x_{n}]^{T}$ 为决策向量； $A=(a_{ij})_{m*n}$ 为约束方程组的系数矩阵； $b=[b_{1},b_{2},...,b_{m}]^{T}$ 为约束方程组的常数向量。

还有标准型：

目标函数为极大型，约束条件为等式约束。满足约束条件的解为可行解，使目标函数达到最大值得可行解角叫最优解。所有可行解构成的集合叫做可行域，记为R。

在数学规划问题求解过程中，一定还要计算灵敏度分析。灵敏度分析指系统因周围条件变化显示出来的敏感程度的分析。线性规划问题的a、b、c都设定为常数，但是在实际过程中，这些系数都会有少许的变动。

模型求解和应用

MATLAB中求解数学规划的问题有两种模式：基于求解器的求解方法和基于问题的求解方法，

基于求解器的求解方法

需要将线性规划化为标准形式：

要求目标函数必须是最小化，约束条件分为小于等于约束和等号约束，lb和ub是决策变量上下界。

MATLAB函数调用格式为：

[x,fval] = linprog(f,A,b)

[x,fval] = linprog(f,A,b,Aeq,beq)

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)

x返回的是决策变量的取值，fval返回的是目标函数的最优值，f为价值向量，A,b对应的是线性不等式约束，Aeq和beq对应的是线性等式的约束，lb和ub分别对应决策向量的下界向量和上界向量。

这种方法只能应用于决策向量是一维的情况。

基于问题的求解方法

首先用变量和表达式构造优化问题，然后用solve函数求解，可以用doc optimproblem查看帮助。

①prob=optimproblem('ObjectiveSense','max');

ObjectiveSense可以是max和min，代表优化最大值还是最小值，默认是min

②定义f，A，b（同上，f可以定义为行向量，这样目标函数不同再转置）

③x=optimvar('x',2,1,'TYPE','integer','LowerBound',0,'UpperBound',inf);

第一个‘x’里面是变量名，列向量，后面是存在几行几列。

‘TYPE’，后面定义的是该函数所属类型，比如说integer整数型，double双精度型号

‘LowerBound'与'UpperBound'表示下界与上界所跟的0，inf分别是范围

④prob.Objective=f * x;%目标函数，目标函数需要得到一个标量数值，不是矩阵向量

⑤prob.Constraints.con=A*x<=b;%约束条件,只有一个约束，也可以不加.con，.con是标签，可以自己命名，多个约束条件时，必须标签不能一样。

⑥[sol fval flag out]=solve(prob);%fval是最优值，sol.x是决策变量的值，当多个决策变量时，可以sol.y，flag在线性规划中不用在意，在非线性规划中注意不能为负值。

例如：

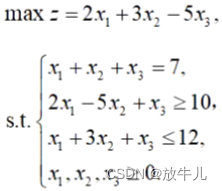
采用求解器求解：

clc,clear
f = [-2;-3;5];%转换为求最小
A = [-2,5,-1;1,3,1];
b = [-10;12];
Aeq = [1,1,1];
beq = [7];
lb = zeros(3,1);
[x,fval] = linprog(f,A,b,Aeq,beq,lb,[]);
x
-fval

x =

6.4286
0.5714
0
ans =

14.5714

采用基于问题的求解

clc,clear
prob=optimproblem('ObjectiveSense','max');
x=optimvar('x',3,'LowerBound',0);
prob.Objective=2*x(1) + 3*x(2) - 5*x(3);
prob.Constraints.con1=2*x(1) - 5*x(2) + x(3)>=10;
prob.Constraints.con2=x(1) + 3*x(2) + x(3)<=12;
prob.Constraints.con3=x(1) + x(2) + x(3)==7;
[sol fval flag out]=solve(prob);
sol.x
fval

ans =

6.4286
0.5714
0
fval =

14.5714

其他

MATLAB中，加载现有的txt文件的矩阵时，若用load函数，则矩阵应每一行列数应该相等。如果缺少个别的数，可使用readmatrix函数。writematrix(a,'data.xlsx')可以写入Excel中。
矩阵索引a(1:end,1)，end就自动是行的最后一列
sum(a,'all')表示矩阵a的所有元素求和