矩阵分解(预测打分)

1.问题引入

 有如下R(5,4)矩阵:("-"表示用户没有打分)
其中打分矩阵R(n,m)是n行和m列，n表示user个数,m表示item个数。

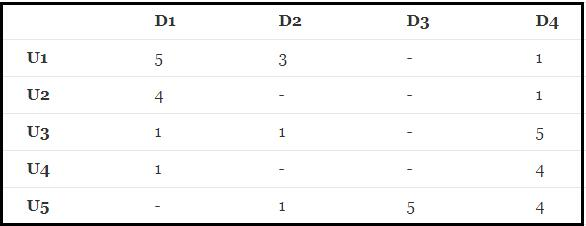
 想要根据目前的矩阵R对未打分的商品进行评分的预测。为了解决这个问题，就用到了矩阵分解的方法。

2.问题分析

2.1构造损失函数

 为了求出未打分的值，可以将矩阵R(n,m)分解为P(n,k)*Q(K,m),所以可以得到一个预测值$\hat{R}=P\ast Q$,来预测矩阵R，那么此时我们的问题就转换成了如何令$\hat{R}$与R最为接近，由此我们引入了损失函数的概念，即让$\hat{R}-R$变小，当小到一定程度后我们即可认为$\hat{R}\approx R$,为了简化计算(令该式子始终大于0)，我们给其加入了一个平方变为
$$Loss(P,Q)=\frac{1}{2}(\widehat{R-R}{)}^2=\frac{1}{2}(\sum _{i=1}^m\sum _{j=1}^n(R_{ij}-\sum _{s=1}^k{P}_{is}{Q}_{js}){)}^2$$

2.1梯度下降

 梯度下降法的核心思想即是沿函数的导数方向的不断改变自身参数，从到最终能到达最低点。梯度下降法的一些注意事项在多元线性回归中做了一些介绍，有兴趣可以查看。
 故运用梯度下降法,先求其偏导数：

$\frac{\partial }{\partial P_{ik}}L(P,Q)$
$=\frac{1}{2}(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})\ast 2\ast (-1)\ast (\frac{\partial {\sum }_{k=1}^k{P}_{ik}{Q}_{kj})}{\partial P_{ik}})$
$=-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})Q_{kj}$
$\frac{\partial }{\partial Q_{kj}}L(P,Q)$
$=\frac{1}{2}(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})\ast 2\ast (-1)\ast (\frac{\partial {\sum }_{k=1}^k{P}_{ik}{Q}_{kj})}{\partial P_{kj}})$
$=-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})P_{ik}$

应用梯度下降法不断修改当前参数值：
$P_{ik}=P_{ik}-\alpha \ast (-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})Q_{kj})$
$=P_{ik}+\alpha (R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})Q_{kj})$

$Q_{kj}=P_{ik}-\alpha \ast (-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})P_{ik})$
$=P_{ik}+\alpha (R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})P_{ik})$
($\alpha$为learning rate ，即学习率)

2.3正则化

 当训练的数据不够时或特征数量大于样本数量时，就会出现过拟合的情况，我们为了解决过拟合，就会采用正则化的手段或者减少一些非必要的样本特征。常用的有L1范数和L2范数。
①LP范数不是一个范数，而是一组范数
$||x|{|}_p=({\sum }_i^n|x_i{|}^p{)}^{\frac{1}{p}}$
②p=1时，几位L1范数
$||x_1||={\sum }_{i=1}^n|x_i|$
②L2范数,平方再开方，表示向量的距离。
$||x_2||=({\sum }_{i=1}^n|x_i{|}^2{)}^{\frac{1}{2}}$
L1正则化：
$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(y^i-h_{\theta }(x^i){)}^2+\lambda \sum _{j=1}n|{\theta }_j|]$$
L2正则化：
$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(y^i-h_{\theta }(x^i){)}^2+\lambda \sum _{j=1}n{\theta }_j^2]$$
式子中m为样本数量，n为特征个数。

3.代码实现

import numpy as np
import matplotlib.pyplot as plt

R=np.array([[5,3,0,1],
            [4,0,0,1],
            [1,1,0,5],
            [1,0,0,4],
            [0,1,5,4]])

M=R.shape[0]
N=R.shape[1]
K=2
P=np.random.rand(M,K)
Q=np.random.rand(K,N)
print(P)
print(Q)

[[0.65360868 0.08726216]
 [0.69762591 0.03076026]
 [0.88861613 0.75595254]
 [0.31559948 0.49104854]
 [0.33077934 0.40914307]]
[[0.68124148 0.49563369 0.14058849 0.73546283]
 [0.31494592 0.86798718 0.48578754 0.95628464]]

$$Loss=\frac{1}{2}(R-PQ{)}^2=\frac{1}{2}(\sum _{i=1}^m\sum _{j=1}^n(R_{ij}-\sum _{s=1}^k{P}_{is}{Q}_{js}){)}^2$$

#损失函数
def cost(R,P,Q):
    e=0
    for i in range(R.shape[0]):
        for j in range(R.shape[1]):
            if(R[i,j]>0):
                e+=(R[i,j]-np.dot(P[i,:],Q[:,j]))**2
                
    return e/2

L2正则化：
$$Loss=\frac{1}{2}(R-PQ{)}^2=\frac{1}{2}(\sum _{i=1}^m\sum _{j=1}^n)R_{ij}-\sum _{s=1}^k{P}_{is}{Q}_{js}{)}^2+\frac{\lambda }{2}\sum _{s=1}k(P_{ik}^2+Q_{kj}^2)$$

#损失函数正则
def cost_re(R,P,Q,lambda1):
    e=0
    for i in range(R.shape[0]):
        for j in range(R.shape[1]):
            if(R[i][j]>0):
                e+=(R[i,j]-np.dot(P[i,:],Q[:,j]))**2
                for k in range(P.shape[1]):
                    e+=lambda1*(P[i,k]**2+Q[k,j]**2)/2    
    return e/2

对损失函数求偏导：
$\frac{\partial }{\partial P_{ik}}L(P,Q)$
$=\frac{1}{2}(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})\ast 2\ast (-1)\ast (\frac{\partial {\sum }_{k=1}^k{P}_{ik}{Q}_{kj})}{\partial P_{ik}})$
$=-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})Q_{kj}$
$\frac{\partial }{\partial Q_{kj}}L(P,Q)$
$=\frac{1}{2}(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})\ast 2\ast (-1)\ast (\frac{\partial {\sum }_{k=1}^k{P}_{ik}{Q}_{kj})}{\partial P_{kj}})$
$=-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})P_{ik}$
梯度下降法：
$P_{ik}=P_{ik}-\alpha \ast (-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})Q_{kj})$
$=P_{ik}+\alpha (R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})Q_{kj})$

$Q_{kj}=P_{ik}-\alpha \ast (-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})P_{ik})$
$=P_{ik}+\alpha (R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})P_{ik})$

#梯度下降
def grad(R,P,Q,lr,epochs):
    costList=[]
    for s in range(epochs+1):
        for i in range(R.shape[0]):
            for j in range(R.shape[1]):
                if(R[i][j]>0):
                    e=R[i,j]-np.dot(P[i,:],Q[:,j])
                    for k in range(P.shape[1]):
                        grad_p=e*Q[k][j]
                        grad_q=e*P[i][k]

                        P[i][k]=P[i][k]+lr*grad_p
                        Q[k][j]=Q[k][j]+lr*grad_q
            
        if s%50==0:
            e=cost(R,P,Q)
            costList.append(e) 
            #print(e)
    return P,Q,costList
lr=0.0001
epochs=10000
p,q,costList=grad(R,P,Q,lr,epochs)
print(np.dot(p,q))

[[5.06116901 2.87426131 2.43375669 1.00254423]
 [3.96425112 2.26334177 2.08974137 0.96504113]
 [1.0366021  0.90360134 5.30277467 4.91333664]
 [0.99043153 0.81279639 4.2952649  3.93863408]
 [1.64541544 1.19616657 4.78417292 4.23883696]]

x=np.linspace(0,10000,201)
plt.plot(x,costList,'r')
plt.xlabel('epochs')
plt.ylabel('cost')
plt.show()

​

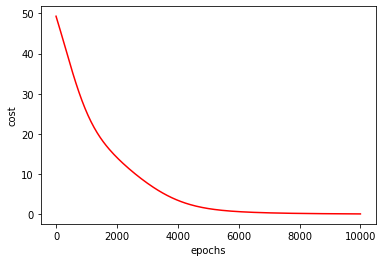
加入正则项后：
$P_{ik}=P_{ik}-\alpha \ast (-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})P_{ik})+\lambda P_{ik}$
$=P_{ik}+\alpha (R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})P_{ik})-\lambda P_{ik}$
$Q_{kj}=Q_{kj}-\alpha \ast (-(R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})Q_{kj})+\lambda Q_{kj}$
$=P_{ik}+\alpha (R_{ij}-{\sum }_{k=1}^k{P}_{ik}{Q}_{kj})Q_{kj})-\lambda Q_{kj}$

#梯度下降（正则）
def grad_re(R,P,Q,lr,epochs,lambda1):
    costList=[]
    for s in range(epochs+1):
        for i in range(R.shape[0]):
            for j in range(R.shape[1]):
                if(R[i][j]>0):
                    e=R[i,j]-np.dot(P[i,:],Q[:,j])
                    for k in range(P.shape[1]):
                        grad_p=e*Q[k][j]#求梯度
                        grad_q=e*P[i][k]

                        #对PQ同时进行梯度下降，改变其值
                        P[i][k]=P[i][k]+lr*grad_p-lambda1*P[i][k]
                        Q[k][j]=Q[k][j]+lr*grad_q-lambda1*Q[k][j]
            
        if s%50==0:#求损失
            e=cost_re(R,P,Q,lambda1)
            costList.append(e) 
            #print(e)
    return P,Q,costList
lambda1=0.0001
p,q,costList=grad_re(R,P,Q,0.003,epochs,lambda1)
print(np.dot(p,q))

[[4.92262848 2.9460198  2.02962105 1.00548811]
 [3.9420148  2.37520018 1.85600337 0.99804788]
 [1.00407789 0.99148638 6.03037773 4.90035828]
 [0.99660486 0.90775439 4.8875762  3.94603309]
 [1.15092516 1.00009806 4.95103649 3.97741499]]

x=np.linspace(0,10000,201)
plt.plot(x,costList,'r')
plt.xlabel('epochs')
plt.ylabel('cost')
plt.show()

​

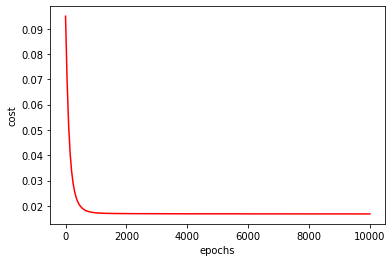
 通过观察代价函数随迭代步数的变化图可以看出：进行正则化后的代价函数的图像比没有进行正则化的图像较为圆滑了些许，可以得出正则化确实是一种解决过拟合问题的一种手段。
 此外，除了正则化以外，还可以通过增加样本数据集的数量或者减少样本特征，抛弃一些不必要的样本特征来避免过拟合。

​