【01】深度学习——数学基础 | 线性代数 | 微积分 |概率

1.线性代数

1.1标量(scalar)

  一个标量就是一个数，它只有大小，没有方向。标量通常用小写字母表示，一些书上会用斜体表示标量，同时在介绍标量的同时会介绍数值类型，例如： $w=3,w\in R$表示人的体重；$n=3,n\in N$表示人的头发。

1.2向量(Vector)

  向量是一组标量排列而成的。向量只有一个轴，沿着行或者列的方向。当一组标量排成一行或者一列的时候，就变成了向量，这些标量的值被称为向量的元素。向量中的元素是按照轴进行有序排列的，这个轴可以是行或者列。
  向量通常用粗体的小写字母表示，向量中的元素可以用带角标的斜体来表示。例如$\mathbf{s}$依次为班里人考试的成绩$\mathbf{s}=\left[\begin{array}{ccccc}{s}_1& s_2& s_2& ...& s_n\end{array}\right]$或$\mathbf{s}=\left[\begin{array}{c}{s}_1\\ s_2\\ s_2\\ ...\\ s_n\end{array}\right]$。

1.2.1模长和范数

  向量的模长：可以简称为向量的模，英文是norm。表示向量在空间中的长度。
  对二维向量$\mathbf{a}=(a_1,a_2)$其模长$||a||=\sqrt{{a_1}^2+{a_2}^2}$
  对n维向量$\mathbf{a}=(a_1,a_2,...,a_n)$其模长等于$||a||=\sqrt{{a_1}^2+{a_2}^2+...+{a_n}^2}$
  范数$||x|{|}_p=({\sum }_i|x_i{|}^p{)}^{\frac{1}{p}}p\in R,p\ge 1$

1.2.2单位向量

  单位向量：是模长固定为1的向量，它通常用来表示的是向量在空间中的方向，而不是大小。
  对二维向量$\mathbf{a}=(a_1,a_2)$其单位向量为$\frac{1}{\sqrt{{a_1}^2+{a_2}^2}}(a_1,a_2)$
  对n维向量$\mathbf{a}=(a_1,a_2,...,a_n)$其单位向量为$\frac{1}{\sqrt{{a_1}^2+{a_2}^2}+...+{a_n}^2}(a_1,a_2,...,a_n)$

1.2.3向量的内积

  内积(Inner Product)：也称为点乘、点积，是两个向量对应位置元素相乘再相加，结果是一个标量。
单价$\mathbf{a}=(a_1,a_2,...,a_n)$
数量$\mathbf{b}=(b_1,b_2,...,b_n)$
总价$\mathbf{c}=\mathbf{a}\cdot \mathbf{b}={\sum }_{i=1}^n{a}_i\cdot b_i$
  内积还可以表示两个向量的线性相关程度，比如将两个向量规范化得到单位向量，二者的内积就是夹角值的余弦，越接近于1则二者更相关，等于0则二者正交（垂直），二者线性无关。

1.2.4向量的外积

  外积(Outer Product):又叫向量叉积、叉乘等。外积的运算结果是一个向量而不像内积是一个标量。
  两个向量的叉积与这两个向量组成的坐标平面垂直，其值取决于$\mathbf{a},\mathbf{b}$的方向和大小，对应计算公式如下：
$$|c|=|a||b|<sin(a,b)>$$

1.3矩阵(Matrix)

  矩阵是由多个元素组成的表格。矩阵是一种二维数据结构，每个数据再矩阵中都有一个对应的行号和列号。矩阵通常用粗体的大写字母表示。
$$\mathbf{A}=\left[\begin{array}{cccc}{A}_{1,1}& A_{1,2}& \cdots & A_{1,n}\\ A_{2,1}& A_{2,2}& \cdots & A_{2,n}\\ ⋮& ⋮& \ddots & ⋮\\ A_{m,1}& A_{m,2}& \cdots & A_{m,n}\end{array}\right]\in R^{m\times n}$$

1.3.1矩阵转置

  矩阵的转置是以主对角线为轴，进行镜像翻转。矩阵转置公式如下(其中T就是Transpos)：
$$\begin{gathered} (\mathbf{A}{)}_{m,n}^T={\mathbf{A}}_{n,m} \\ \mathbf{A}=\left[\begin{array}{cc}{A}_{1,1}& A_{1,2}\\ A_{2,1}& A_{2,2}\\ A_{3,1}& A_{3,2}\end{array}\right]A^T=\left[\begin{array}{ccc}{A}_{1,1}& A_{1,2}& A_{3,1}\\ A_{1,2}& A_{2,2}& A_{3,2}\end{array}\right] \end{gathered}$$

1.3.2矩阵乘法

  有m行k列的矩阵A和k行n列的矩阵B
$$\mathbf{A}=\left[\begin{array}{cccc}{A}_{1,1}& A_{1,2}& \cdots & A_{1,k}\\ A_{2,1}& A_{2,2}& \cdots & A_{2,k}\\ ⋮& ⋮& \ddots & ⋮\\ A_{m,1}& A_{m,2}& \cdots & A_{m,k}\end{array}\right]\mathbf{B}=\left[\begin{array}{cccc}{B}_{1,1}& B_{1,2}& \cdots & B_{1,n}\\ B_{2,1}& B_{2,2}& \cdots & B_{2,n}\\ ⋮& ⋮& \ddots & ⋮\\ B_{k,1}& B_{k,2}& \cdots & B_{k,n}\end{array}\right]$$
  矩阵$\mathbf{A}$和矩阵$\mathbf{B}$相乘，则A的列数必须和B的行数相等，此时：
$$\mathbf{C}=\mathbf{A}\otimes \mathbf{B}=\mathbf{AB}\Rightarrow C_{m,n}=\sum _k{A}_{m,k}Bk,n$$
  矩阵乘法是有顺序的。
  矩阵内积：结果是一个标量，等于两个矩阵AB对应元素之间相乘再相加。对应公式如下：
$$c=\sum _{i=1}^m\sum _{j=1}^n{A}_{i,j}{B}_{i,j}$$
  哈达玛积(Hadamard product)：两个矩阵AB对应元素直接相乘，结果是一个矩阵。
$$\mathbf{C}=\mathbf{A}\odot \mathbf{B}\Rightarrow \mathbf{C}=\left[\begin{array}{cccc}{A}_{1,1}{B}_{1,1}& A_{1,2}{B}_{1,2}& \cdots & A_{1,n}{B}_{1,n}\\ A_{2,1}{B}_{2,1}& A_{2,2}{B}_{2,2}& \cdots & A_{2,n}{B}_{2,n}\\ ⋮& ⋮& \ddots & ⋮\\ A_{m,1}{B}_{m,1}& A_{m,2}{B}_{m,2}& \cdots & A_{m,n}{B}_{m,n}\end{array}\right]$$

1.3.3矩阵乘法的性质

  交换律：$\mathbf{AB}\ne \mathbf{BA}$
  分配律：$\mathbf{A}(\mathbf{B}+\mathbf{C})=\mathbf{AB}+\mathbf{AC}$
  结合律：$(\mathbf{AB})\mathbf{C}=\mathbf{A}(\mathbf{BC})$
  转置性质：$(\mathbf{AB}{)}^T={\mathbf{B}}^T{\mathbf{A}}^T$

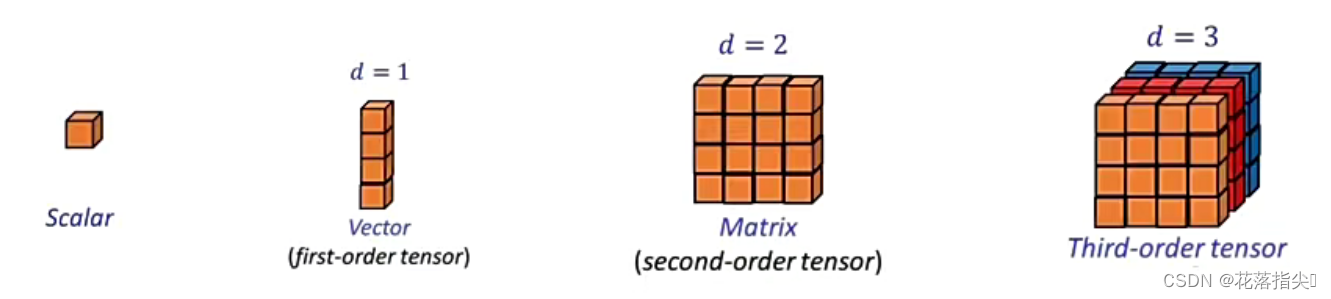
1.4张量（Tensor）

  张量是多为数组的抽象概括，可以看作是向量和矩阵的推广。
  向量和矩阵的运算方法对张量同样适用。

2.微积分

  微积分内容包含了微分学、积分学及相关概念和应用。
  微积分研究连续函数，曲线和曲面的性质。
  微积分广泛应用于深度学习领域，如梯度下降法。

2.1极限

  表示某一点出函数值趋近于某一特定值的过程，一般记为：
$$\underset{x\to a}{\lim }f(x)=L$$
  极限是一种变化状态的描述，核心思想是无限靠近而永远不能到达。

2.2导数

  导数是函数的局部性质，指一个函数在某一点附近的变化率，对函数$y=f(x)$来说，他的导数可以用符号$f^{\prime }(x)$来表示，也可记为$\frac{df(x)}{dx}$。

2.2.1导数和极限

  对函数$f(x)=\frac{x^3-3x^2+6}{2}$，图像如下所示：

  计算x=2处的导数可得：
$$\begin{gathered} f^{\prime }(2)=\underset{h\to 0}{\lim }\frac{f(2+h)-f(2)}{h} \\ h值：1.0000000,极限值：2.0000000 \\ h值：0.1000000,极限值：0.1550000 \\ h值：0.0100000,极限值：0.0150500 \\ h值：0.0010000,极限值：0.0015005 \\ h值：0.0001000,极限值：0.0001500 \\ h值：0.0000100,极限值：0.0000150 \\ h值：0.0000010,极限值：0.0000015 \\ h值：0.0000001,极限值：0.0000002 \end{gathered}$$

2.2.2导数和极限

  常见导数计算公式：
  常数函数$f(x)=C{f}^{\prime }(x)=0$
  幂函数 $f(x)=x^n{f}^{\prime }(x)=n{x}^{n-1}$
  指数函数$f(x)=e^x{f}^{\prime }(x)=e^x$
  对数函数$f(x)=ln(x)f^{\prime }(x)=\frac{1}{x}$

2.3微分

  微分是指对函数得局部变化的一种线性描述，自变量的微分记作$dx$,函数$y=f(x)$的微分记作$dy=df(x)=f^{\prime }(x)dx$。
  导数是微分的比值，$f^{\prime }(x)=\frac{df(x)}{dx}$。
  导数表示变化率(rate)，微分表示变化量(dy或dx)。

2.4偏导数

  偏导数指的是多元函数在莫一点处关于某一变量的导数。
  通常用符号$\frac{\partial f(x,y)}{\partial x}$来表示多元函数$z=f(x,y)$关于x的偏导数，即：
$$\frac{\partial f(x,y)}{\partial x}=\underset{h\to 0}{\lim }\frac{f(x+h,y)-f(x,y)}{h}$$

2.5梯度

  梯度可以理解为一个包含所有偏导数的向量，符号是$\nabla$
  对函数$z=f(x,y)=x^2+y^2$来说，它的梯度向量是:
$$\nabla f(x,y)=(2x,2y)$$
  梯度下降算法中，参数更新公式为（其中$\eta$为学习率）：
$${\theta }_{t+1}={\theta }_t-\eta {\nabla }_{\theta }\mathcal{J}({\theta }_t)$$

2.6链式法则

  链式法则是用来计算复合函数导数的。
  假设对实数x，有可微函数f和g，其中$z=f(y),y=g(x)$那么，链式法则公式如下：
$$\frac{dz}{dx}=\frac{dz}{dy}\cdot \frac{dy}{dx}$$
  所谓的链式法则，就是一层一层增加可以“相互抵消”的分子分母。
  有函数$f(x)=x^2$和$g(x)=x+1$，计算$h(x)=f(g(x))=(x+1{)}^2$的导数，可得：
$$\begin{array}{rl}{h}^{\prime }(x)& =f(g(x))\cdot g^{\prime }(x)\\ & =2(x+1)\cdot 1\\ & =2x+2\end{array}$$

3.概率

  概率是一种用来描述随机事件发生的可能性的数字度量。
  概率并不客观存在。
  概率是一种不确定性的度量。

3.1概率和深度学习

  概率可以用来表示模型的准确率（错误率）。
  概率可以用来描述模型的不确定性。
  概率可以作为模型损失的度量。

3.2概率的研究

  频率学派——愚公移山的智慧（多次实验）。代表人物Jakob Bernoulli。
  频率学派计算公式如下：
$$\begin{array}{rl}{P}_n(x)& =\frac{n_x}{n}\\ P(x)& =\underset{n\to \infty }{\lim }{P}_n(x)\end{array}$$
  古典学派——平均主义的倡导者。
  无法掌握先验知识的情况下，未知事件发生的概率都是相等的。其公式如下（其中m是x包含基本事件的个数，n是基本事件的总数）：
$$\begin{array}{rl}P(x)& =\frac{m}{n}\end{array}$$
  贝叶斯学派——探索未知世界的观察者。
  频率学派认为概率是随机性，贝叶斯派认为概率是不确定性。
  概率是个人的主观概念，表面我们对事务的相信程度，通过观测得到的数据对结果进行更新，从而得到更为准确的估计。

3.3概率和统计

  概率研究的是一次事件的结果。
  统计研究的是总体数据的情况。
  概率是统计的基础，统计则根据观测的数据反向思考其数据生成过程。

3.3.1事件(Event)

  事件相当于实验的结果。
  随机事件其实是一次或多次随机试验的结果。
  事件的基本属性包括：可能性，确定性，兼容性。
  依赖事件指的是事件的发生受其他事件影响。
  独立事件指的是事件的发生与其他事件无关。

3.3.2随机变量和概率分布

  随机变量是概率统计中用来表示随机事件结果的变量。
  随机标量包括离散随机变量和连续随机变量。
  概率分布用来描述随机变量的分布情况。

3.3.3概率密度

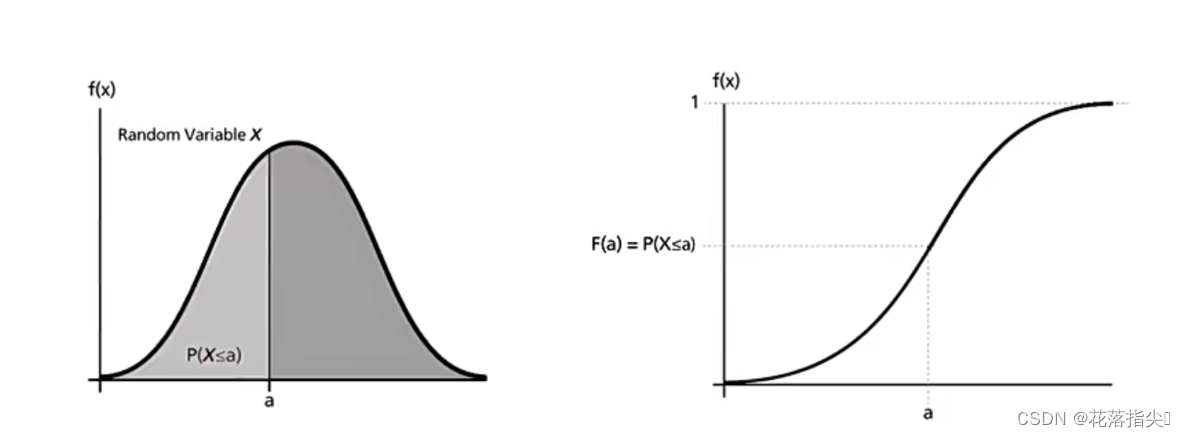
  概率密度（probability density）是一种描述概率分布的函数。它表示在某一区间内取一个特定值的概率。
  概率 = 概率密度曲线下的面积(CDF，cumulative probability density function)。
  正态分布概率密度函数如下：
$$\begin{array}{r}f(x)=(\frac{1}{\sqrt{2\pi {\sigma }^2}}exp(-\frac{x-{\mu }^2}{2{\sigma }^2}))\end{array}$$

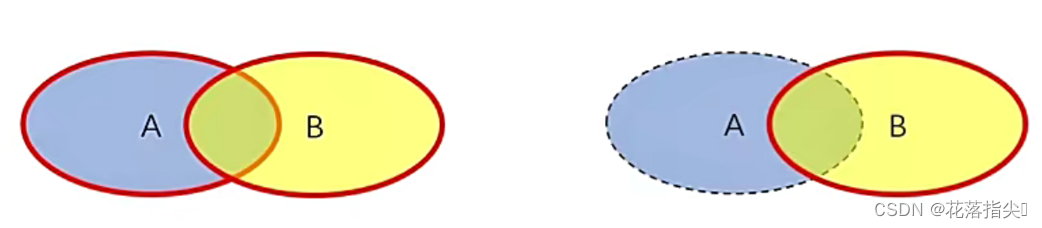
3.3.4联合概率和条件概率

  联合概率是指同时发生两个或多个事件的概率，记为$P(A,B)$。
  条件概率是指在某个条件下发生某个事件的概率，记为$P(A|B)$。

  联合概率和条件概率相互转化：
$$\begin{array}{rl}P(A,B)& =P(A|B)P(B)\\ P(A|B)& =\frac{P(A,B)}{P(B)}\end{array}$$

3.4贝叶斯定理

  贝叶斯定理表明在已知条件概率的情况下，可以推导出联合概率。常用于根据已知信息推测未知信息的场景，公式如下：
$$\begin{array}{r}P(A|B)=\frac{P(B|A)P(A)}{P(B)}\end{array}$$
  其中$P(A)$和$P(B)$称为先验概率，$P(B)$为Evidence，$P(A)$为prior，$P(A|B)$称为后验概率posterior，$P(B|A)$称为可能性likelihood。

3.5极大似然估计

  Maximum Likelihood Estimation，MLE：利用已知的样本结果，反推最优可能导致这样结果的参数，即找到参数的最大概率取值。

  对于给定的样本集$X=x_1,x_2,...,x_n$我们需要估计参数向量$\theta$，此时可以计算似然函数$L(\theta )$，等于联合概率密度函数$p(X|\theta )$。公式表示如下：
$$\begin{array}{r}L(\theta )=p(X|\theta )=\prod _{i=1}^{n}p(x_i|\theta )\end{array}$$