基尔霍夫衍射理论

一、矢量理论到标量理论

前提条件：介质同时具有线性、各向同性、均匀性且无色散。

结论：电场和磁场的所有分量的行为完全相同，可由单一的一个标量波动方程描述，标量理论可以完全准确的代替矢量理论。

若介质不具备上述前提，则用标量理论来表征矢 量理论就会引入误差。

二、惠更斯－菲涅耳原理

2.1 惠更斯原理：子波的概念

        波前上的每一个面元都可以看作是一个次级扰动中心，它们能产生球面子波，并且，后一时刻的波前的位置是所有这些子波前的包络面。

2.2 惠更斯－菲涅耳原理

子波（次波）相干叠加

        其中， (P) 是波面上任意一点P的复振幅，U(Q)是光场种任一观察点Q的复振幅，r是P到Q的距离，是PQ和过P点的元波面法线n的夹角，K() 是与有关的倾斜因子，c 为常数。

三、基尔霍夫衍射积分公式

        基尔霍夫利用数学上的格林定理, 通过假定衍射屏的边界条件, 求解波动方程, 导出了平面衍射屏的衍射积分公式。

3.1 基尔霍夫边界条件

         在孔径Σ上，场分布U及其导数跟没有屏幕时完全相同；在的位于屏幕的几何阴影区域内的那一部分，场分布U及其导数恒为零。

3.2 基尔霍夫衍射积分公式

如下式：

         单色点光源位于处, P为孔径平面Σ上任一点, Q为孔径后方的观察点，r和分别是 Q和到P的距离, n表示Σ 面上法线的正方向。

        上述基尔霍夫衍射公式仅仅是单个球面波照明孔径的情况作出的讨论，但衍射公式却适用于更普遍的任意单色光波照明孔径的情况。因为任意复杂的光波可分解成简单的球面波的线性组合，波动方程的线性性质允许对每一单个球面波分别应用上述原理，再把所有点源在Q点的贡献叠加。因此， 基尔霍夫衍射公式中（P）可以理解为在任意单色光照明下在孔径平面产生的光场分布。

3.3 衍射与障碍物

        不论以什么方式改变光波波面——（1）限制波面范围，（2）振幅以一定分布衰减，（3）以一定的空间分布使复振幅相位延迟，（4）相位与振幅两者兼而变化，都会引起衍射，均称为衍射。

        所以障碍物的概念，除去不透明屏上有开孔这种情况以外，还包含具有一定复振幅的透明片。把能引起衍射的障碍物统称为衍射屏。

         基尔霍夫衍射积分公式是在无限大不透光屏上有一开孔的情况下导出的，但可以推广到其它任何复杂的衍射屏。只是此时, 公式中

         （P）是衍射屏前表面的复振幅或照射到衍射屏上的光场的复振幅；

        （P）是衍射屏后表面的复振幅。

        能引起衍射的障碍物统称为衍射屏, 描写衍射屏自身宏观光学性质的是它的复振幅透过率 t ( P )。

3.4 惠更斯－菲涅耳原理与叠加积分

基尔霍夫衍射衍射积分公式为

        此式是一个叠加积分，满足线性系统的叠加性和均匀性。因此衍射过程（光波从衍射平面到观察平面的传播过程）可以看作是一个线性系统。（P）是输入，U(Q)是输出。

        h(P,Q)是该线性系统的脉冲响应（点扩散系统）

         h(P,Q)可看作是：衍射屏上点P的一个单位脉冲在场点Q产生的复振幅分布, 它描述了衍射系统的特性。它具有点源球面波的特性, 它就是惠更斯-菲涅耳原理中的次波源发出的次级球面波。若把衍射过程看成是 一个线性系统, 惠更斯-菲涅耳原理中的次级球面波就是这个系统的脉冲响应。

3.5 相干光场在自由空间传播的平移不变性

         当点光源与场点 Q距离衍射屏足够远 (即 , z足够大) ，且观察范围较小, 即

观察点Q到孔径平面上任一点P的距离

         这表明, 在满足一定条件下, 衍射屏上各次波源在场点Q处所产生的复振幅分布具有相同的分布形式, 只是发生了一个空间平移。即：具有平移不变性。 可写成卷积的形式

         观察面上的光场分布, 等于衍射屏后的光场分布和系统脉冲响应的卷积。

四、菲涅耳近似(傍轴近似) 菲涅耳衍射

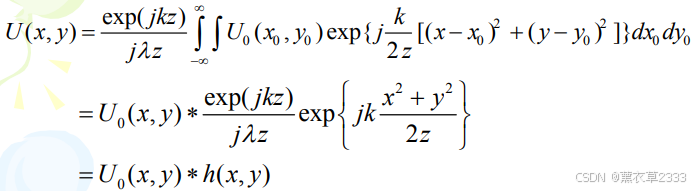
 上式为空域中的菲涅耳衍射的积分公式。

上式为菲涅耳衍射的脉冲响应。菲涅耳衍射的脉冲响应, 仍具有平移不变性。

五、夫琅禾费近似(远场近似)-夫琅和费衍射

        上式为衍射光场。 从上式可以看出，夫琅和费衍射仍是线性系统，但不是平移不变系统，不再具有平移不变性。当z变化时，衍射图样只是按比例放大或缩小，图样形状不会发生变化。

上式为脉冲响应。 不再具有平移不变性。