【Python数学建模常用算法代码（九）之层次分析法】

代码模板在最后！！！！！！

什么是层次分析法

层次分析法，简称AHP，是指将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初，在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。
层次分析法是指将一个复杂的多目标决策问题作为一个系统，将目标分解为多个目标或准则，进而分解为多指标（或准则、约束）的若干层次，通过定性指标模糊量化方法算出层次单排序（权数）和总排序，以作为目标（多指标）、多方案优化决策的系统方法。

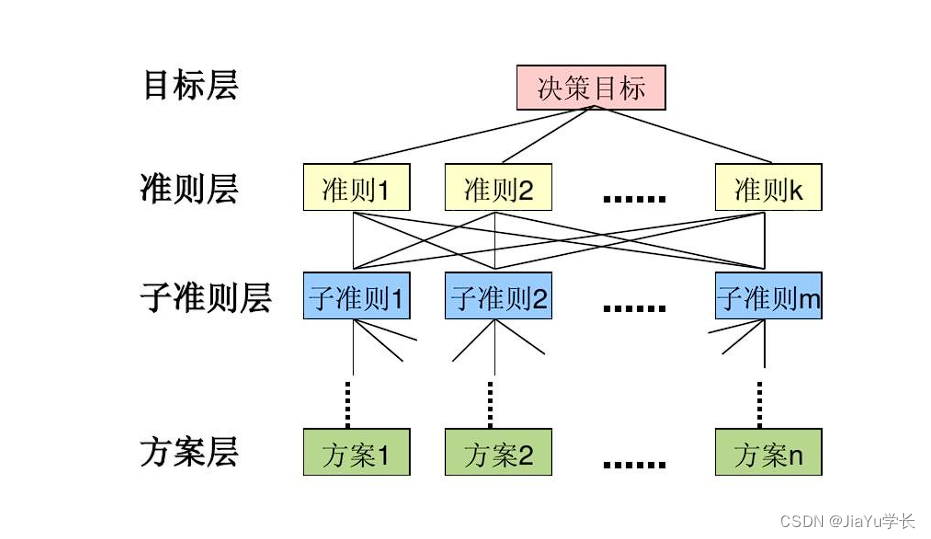
层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。

层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。

基本原理

层次分析法根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型，从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。

层次分析法干什么用

在对社会、经济以及管理领域的问题进行系统分析时，面临的经常是一个由相互关联、相互制约的众多因素构成的复杂系统。层次分析法则为研究这类复杂的系统，提供了一种新的、简洁的、实用的决策方法。

层次分析法主要应用在安全科学和环境科学领域。在安全生产科学技术方面主要应用包括煤矿安全研究、危险化学品评价、油库安全评价、城市灾害应急能力研究以及交通安全评价等；在环境保护研究中的应用主要包括：水安全评价、水质指标和环境保护措施研究、生态环境质量评价指标体系研究以及水生野生动物保护区污染源确定等。除此之外，层次分析法更多的可以用于指导和解决个人生活中遇到的问题，比如说专业的选择、工作的选择以及买房的选择等，可以通过建立层次结构以及衡量指标，来理清工作思路和思考问题的层面。

注意事项

在运用层次分析法时，如果所选的要素不合理，其含义混淆不清，或要素间的关系不正确，都会降低AHP法的结果质量，甚至导致AHP法决策失败。为保证递阶层次结构的合理性，需把握以下原则：
分解简化问题时把握主要因素，不漏不多；
注意相比较元素之间的强度关系，相差太悬殊的要素不能在同一层次比较。

代码模板

import numpy as np
class AHP:
    """
    相关信息的传入和准备
    """

    def __init__(self, array):
        ## 记录矩阵相关信息
        self.array = array
        ## 记录矩阵大小
        self.n = array.shape[0]
        # 初始化RI值，用于一致性检验
        self.RI_list = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58,
                        1.59]
        # 矩阵的特征值和特征向量
        self.eig_val, self.eig_vector = np.linalg.eig(self.array)
        # 矩阵的最大特征值
        self.max_eig_val = np.max(self.eig_val)
        # 矩阵最大特征值对应的特征向量
        self.max_eig_vector = self.eig_vector[:, np.argmax(self.eig_val)].real
        # 矩阵的一致性指标CI
        self.CI_val = (self.max_eig_val - self.n) / (self.n - 1)
        # 矩阵的一致性比例CR
        self.CR_val = self.CI_val / (self.RI_list[self.n - 1])

    """
    一致性判断
    """

    def test_consist(self):
        # 打印矩阵的一致性指标CI和一致性比例CR
        print("判断矩阵的CI值为：" + str(self.CI_val))
        print("判断矩阵的CR值为：" + str(self.CR_val))
        # 进行一致性检验判断
        if self.n == 2:  # 当只有两个子因素的情况
            print("仅包含两个子因素，不存在一致性问题")
        else:
            if self.CR_val < 0.1:  # CR值小于0.1，可以通过一致性检验
                print("判断矩阵的CR值为" + str(self.CR_val) + ",通过一致性检验")
                return True
            else:  # CR值大于0.1, 一致性检验不通过
                print("判断矩阵的CR值为" + str(self.CR_val) + "未通过一致性检验")
                return False

    """
    算术平均法求权重
    """

    def cal_weight_by_arithmetic_method(self):
        # 求矩阵的每列的和
        col_sum = np.sum(self.array, axis=0)
        # 将判断矩阵按照列归一化
        array_normed = self.array / col_sum
        # 计算权重向量
        array_weight = np.sum(array_normed, axis=1) / self.n
        # 打印权重向量
        print("算术平均法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight

    """
    几何平均法求权重
    """

    def cal_weight__by_geometric_method(self):
        # 求矩阵的每列的积
        col_product = np.product(self.array, axis=0)
        # 将得到的积向量的每个分量进行开n次方
        array_power = np.power(col_product, 1 / self.n)
        # 将列向量归一化
        array_weight = array_power / np.sum(array_power)
        # 打印权重向量
        print("几何平均法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight

    """
    特征值法求权重
    """

    def cal_weight__by_eigenvalue_method(self):
        # 将矩阵最大特征值对应的特征向量进行归一化处理就得到了权重
        array_weight = self.max_eig_vector / np.sum(self.max_eig_vector)
        # 打印权重向量
        print("特征值法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight


if __name__ == "__main__":
    # 给出判断矩阵
    b = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]])

    # 算术平均法求权重
    weight1 = AHP(b).cal_weight_by_arithmetic_method()
    # 几何平均法求权重
    weight2 = AHP(b).cal_weight__by_geometric_method()
    # 特征值法求权重
    weight3 = AHP(b).cal_weight__by_eigenvalue_method()