层次分析法详细讲解+Python代码实现

艾派森

已于 2024-08-02 09:12:03 修改

阅读量1.1w

点赞数 100

分类专栏：数学建模文章标签： python 算法数据分析数据挖掘

于 2024-07-13 16:41:04 首次发布

本文链接：https://blog.csdn.net/m0_64336780/article/details/138449353

版权

数学建模专栏收录该内容

7 篇文章

订阅专栏

🤵‍♂️ 个人主页：@艾派森的个人主页

✍🏻作者简介：Python学习者
🐋 希望大家多多支持，我们一起进步！😄
如果文章对你有帮助的话，
欢迎评论 💬点赞👍🏻 收藏 📂加关注+

问题的提出

日常生活中有很多的决策问题。决策是指在面临多种方案时需要依据一定的标准选择某一种方案。

买衣服，一般要依据质量、颜色、价格、款式等方面的因素选择
旅游，是去风光秀丽的苏州，还是去迷人的北戴河，或者是去山水甲天下的桂林，那一般会依据景色、费用、食宿条件、旅途等因素来判断去哪个地方

研究问题：XX微博要选出一个明星作为微博之星，现在有三个候选明星A、B、C，该选择哪位明星呢?

考虑一个明星的成就可以看其粉丝数、颜值、作品数量、作品质量(考虑用作品某瓣平均评分代替)
A、B、C的相关数据如下：

思考：XX微博要选出一个明星作为微博之星，现在有三个候选明星A、B、C，该选择哪位明星呢?
怎么能让指标在同一数量级，且保证在同一指标下其差距不变?
归一化处理：指标的数组[a b c]归一化处理得到[a/(a+b+c)，b/(a+b+c)，c/(a+b+c)]

明星A当选吗？实际上每个指标的重要性是不同的。

来给每一个指标加上权重，微博公司考虑宣传效果，认为粉丝数最重要，作品数量最不重要。比如给人为的给粉丝数设定0.4的权重....

这个方法大家肯定不陌生，比如在大学中的课程成绩，一般卷面成绩占比70%，平时成绩占比30%等，最后得到的成绩就是综合卷面成绩和平时成绩加权后的总分。

思考：这里我是随机设置的权重，如何科学地设定权重？

层次分析法

面临各种各样的方案，要进行比较、判断、评价、直至最后的决策。这个过程中都是一些主观的因素，这些因素可能由于个人情况的不同，有相应不同的比重，所以这样主观因素给数学方法的解决带来了很多的不便

基本概念

层次分析法(Analytic HierarchyProcess，简称AHP)是对一些较为复杂、较为模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题它是美国运筹学家 T.L. Saaty 教授于上世纪 70年代初期提出的一种简便、灵活而又实用的多准则决策方法。

模型原理

应用 AHP 分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。在这个模型下，复杂问题被分解为元素的组成部分。这些元素又按其属性及关系形成若干层次。上一层次的元素作为准则对下一层次有关元素起支配作用。这些层次可以分为三类:·

最高层：这一层次中只有一个元素，一般它是分析问题的预定目标或理想结果，因此也称为目标层。
中间层：这一层次中包含了为实现目标所涉及的中间环节，它可以由若千个层次组成，包括所需考虑的准则、子准则，因此也称为准则层·
最底层：这一层次包括了为实现目标可供选择的各种措施、决策方案等，因此也称为措施层或方案层。

对于我们刚刚提出的问题来说，目标层就是选出微博之星；中间层就是判断方案好坏的指标，对应的就是粉丝数、作品质量、作品数量等；最底层就是对应的A、B、C三位明星。

基本步骤

运用层次分析法建模，大体上可按下面四个步骤进行：

建立递阶层次结构模型
构造出各层次中的所有判断矩阵
一致性检验
求权重后进行评价

我们还是以选出微博之星的问题为例

①建立递阶层次结构模型

其递阶层次结构模型如下：

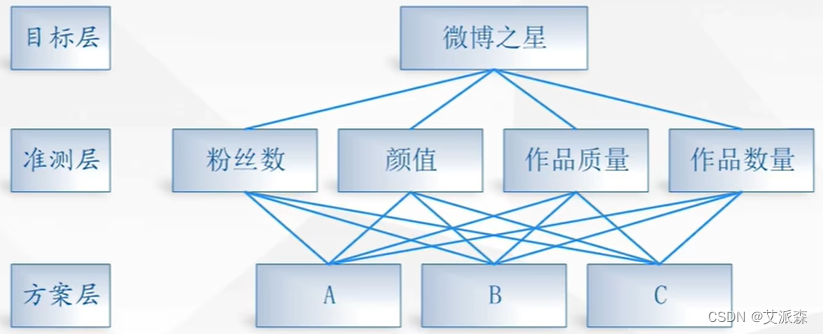
②构造出各层次中的所有判断矩阵

对指标的重要性进行两两比较，构造判断矩阵，从而科学求出权重
矩阵中元素 $eq?a_%7Bij%7D$ 的意义是，第i个指标相对第j个指标的重要程度

构造判断矩阵

粉丝数跟作品数量比显然明显重要，那么 $eq?a_%7B14%7D%3D5$ ，反过来，作品数量相比粉丝数的重要性那就是1/5。

以此对变量进行两两比较，得到完整的判断矩阵，如下表：

因两两比较的过程中忽略了其他因素，导致最后的结果可能出现矛盾。

如上表可以看出 $eq?a_%7B23%7D$ =1/2代表在重要性上，颜值不如作品质量; $eq?a_%7B24%7D$ =2代表着颜值比作品数量重要,因此可以看出作品质量比作品数量重要，但 $eq?a_%7B34%7D$ =1/2意味着作品质量不如作品数量重要，与上一条矛盾！所以需要一致性检验！

③一致性检验

一致矩阵

若矩阵中每个元素 $eq?a_%7Bij%7D$ >0且满足 $eq?a_%7Bij%7D%5Ctimes%20a_%7Bji%7D%3D%201$ ，则我们称该矩阵为正互反矩阵。在层次分析法中，我们构造的判断矩阵均是正互反矩阵。若正互反矩阵满足 $eq?a_%7Bik%7D%5Ctimes%20a_%7Bkj%7D%5Cdoteq%20a_%7Bij%7D$ ，则我们称其为一致矩阵。比如下面这个矩阵就是一致矩阵。

注意：在使用判断矩阵求权重之前，必须对其进行一致性检验，以免产生矛盾。

一致性检验原理：检验我们构造的判断矩阵和一致矩阵是否有太大差别。

一致性检验步骤：

1.计算一致性指标CI

$eq?CI%3D%20%5Cfrac%7B%5Clambda%20_%7Bmax%7D-n%7D%7Bn-1%7D$

2.查找对应的平均随机一致性指标RI

注：RI我们只需要会查表即可，不用管怎么来的。在实际运用中，n很少超过10，如果指标的个数大于10，则可考虑建立二级指标体系，或者使用模糊综合评价模型。

3.计算一致性比例CR

现在回到微博之星那个问题

当前判断矩阵的 $eq?%5Clambda%20_%7Bmax%7D$ =4.68，n=4，求得CI=0.227，查表RI=0.89，得CR=0.255，CR >0.1，需修改判断矩阵。

修改后判断矩阵如下：

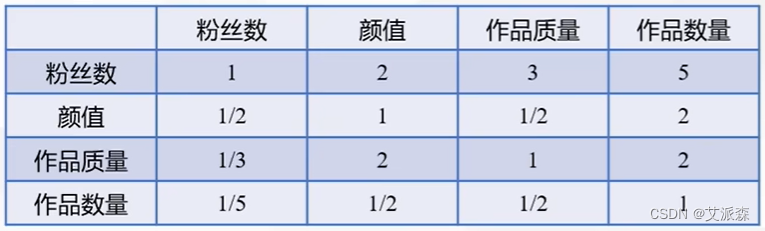
当前判断矩阵的 $eq?%5Clambda%20_%7Bmax%7D$ =4.1128，n =4，求得CI=0.227，查表RI=0.89，得CR=0.0418，CR<0.1，通过一致性检验。

④求权重

方法一：算术平均法求权重

第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
第二步:将归一化的各列相加(按行求和)
第三步:将相加后得到的向量中每个元素除以n即可得到权重向量

用算术平均法求出微博之星的指标权重如下：

方法二：几何平均法求权重

第一步:将判断矩阵的元素按照行相乘得到一个新的列向量
第二步:将新的向量的每个分量开n次方
第三步:对该列向量进行归一化即可得到权重向量

用几何平均法求出微博之星的指标权重如下：

方法三：特征值法求权重

假如我们的判断矩阵一致性可以接受，那么我们可以仿照一致矩阵权重的求法。

第一步:求出矩阵A的最大特征值以及其对应的特征向量
第二步:对求出的特征向量进行归一化即可得到我们的权重

最大特征值为4.1128 一致性比例CR=0.1128/3=0.04

其对应的特征向量:[0.8487 0.3076 0.3962 0.1676]

对其进行归一化得到权重:[0.493 0.179 0.230 0.097]

求评分

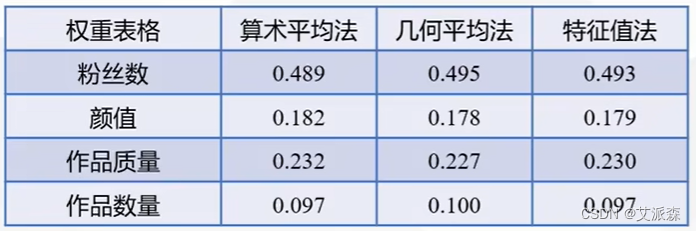
三种方法求得的权重基本上都差不多，那这里我们就用特征值法来求。

如果选择特征值法，综合评分=0.493*粉丝数+0.179*颜值+0.230*作品质量+0.097*作品数量

从最终评分结果来看，还是明星A获胜，应当选微博之星！

Python代码实现

首先是一致性检验，我们以前面的案例中的判断矩阵为例进行演示，首先使用原先的判断矩阵

import numpy as np
# 定义矩阵A，np.array 是 umpy 库中的一个函数，用于创建数组。它将输入的对象(如列表、元组、其他数组等)转换为 Mumpy 数组。
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,1/2],[1/5,1/2,2,1]]) # 原判断矩阵
n = A.shape[0] # 获取A的行，0变为1则是获取A的列，shape是获取形状信息

# 求出最大特征值以及对应的特征向量，np.linalg.eig是NumPy 库中的一个函数，用于计算方阵的特征值和特征向量。
eig_val,eig_vec = np.linalg.eig(A) # eig_val是特征值，eig_vec是特征向量
Maxeig = max(eig_val) # 求特征值的最大值

CI = (Maxeig-n)/(n-1)
RI = [0,0.0001,0.52,0.89,1.12,1.26,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58, 1.59] 
# 注意哦，这里的RI最多支持n=15
# 这里n=2时，一定是一致矩阵，所以CI =0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数

CR = CI/RI[n-1]
print('一致性指标CI =',CI)
print('一致性比例CR =',CR)
if CR< 0.10:
    print('因为CR<0.10，所以该判断矩阵A的一致性可以接受!')
else:
    print('注意:CR>= 0.10，因此该判断矩阵A需要进行修改!')

代码运行结果如下：

将代码中的判断进行修改

A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]]) # 修改后的判断矩阵

重新运行结果如下：

接着求权重

方法一：算术平均法求权重

import numpy as np
# 定义判断矩阵A
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])
# 计算每列的和
# np.sum 函数可以计算一维数组中所有元素的总和。
# 还可以通过指定 axis 參数来计算多维数组的某个维度上的元素总和。例如，在二维数组中，axis=0 表示按列计算总和，axis=1 表示按行计算总和。
ASum = np.sum(A, axis=0)
# 获取A的行和列
n = A.shape[0]
# 归一化，二维数组除以一维数组，会自动将一维数组扩展为与二维数组相同的形状，然后进行逐元素的除法运算。
stand_A = A/ASum
# 各列相加到同一行
ASumr = np.sum(stand_A, axis=1)
#计算权重向量
weights = ASumr/n
print('算术平均法求的权重结果为：',weights)

代码运行结果：

方法二：几何平均法求权重

import numpy as np
# 定义判断矩阵A
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])
# 获取A的行和列
n = A.shape[0]
# 将A中每一行开素相乘得到一列向量
# np.prod 函数可以计算一维数组中所有元素的乘积。
# 还可以通过指定 axis 參数来计算多维数组的某个维度上的元素柔积。例如，在二维数组中，axis=0 表示按列计算乘积，axis=1 表示按行计算乘积。
prod_A = np.prod(A, axis=1)
# 将新的向量的每个分量开n次方等价求1/n次方
# np.power是NumPy库中的一个函数，用于对数组中的元素进行运。
# 例如，可以使用np.power(a，b)对数组a中的每个元素都按照b指数进行运算。
prod_n_A=np.power(prod_A, 1/n)
# 归一化处理
re_prod_A= prod_n_A/ np.sum(prod_n_A)
# 打印权重结果
print('几何平均法求的权重结果为：',re_prod_A)

代码运行结果：

方法三：特征值法求权重

import numpy as np
# 定义判断矩阵A
A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])
# 获取A的行
n = A.shape[0]
# 求出特征值和特征向量
eig_values,eig_vectors = np.linalg.eig(A)
# 找出最大特征值的索引，np.argmax是umPy库中的一个函数，用于返回数组中最大值的索引
max_index = np.argmax(eig_values)
# 找出对应的特征向量
max_vector = eig_vectors[:, max_index]
# 对特征向量进行归一化处理,得到权重
weights = max_vector /np.sum(max_vector)
# 输出权重
print('特征值法求的权重结果为：',weights)

最后，我们将前面的一致性检验和求权重代码进行汇总，编写一个层次分析法的类，用来求权重

import numpy as np
class AHP:
    """
    相关信息的传入和准备
    """

    def __init__(self, array):
        ## 记录矩阵相关信息
        self.array = array
        ## 记录矩阵大小
        self.n = array.shape[0]
        # 初始化RI值，用于一致性检验
        self.RI_list = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58,1.59]
        # 矩阵的特征值和特征向量
        self.eig_val, self.eig_vector = np.linalg.eig(self.array)
        # 矩阵的最大特征值
        self.max_eig_val = np.max(self.eig_val)
        # 矩阵最大特征值对应的特征向量
        self.max_eig_vector = self.eig_vector[:, np.argmax(self.eig_val)].real
        # 矩阵的一致性指标CI
        self.CI_val = (self.max_eig_val - self.n) / (self.n - 1)
        # 矩阵的一致性比例CR
        self.CR_val = self.CI_val / (self.RI_list[self.n - 1])

    """
    一致性判断
    """

    def test_consist(self):
        # 打印矩阵的一致性指标CI和一致性比例CR
        print("判断矩阵的CI值为：" + str(self.CI_val))
        print("判断矩阵的CR值为：" + str(self.CR_val))
        # 进行一致性检验判断
        if self.n == 2:  # 当只有两个子因素的情况
            print("仅包含两个子因素，不存在一致性问题")
        else:
            if self.CR_val < 0.1:  # CR值小于0.1，可以通过一致性检验
                print("判断矩阵的CR值为" + str(self.CR_val) + ",通过一致性检验")
                return True
            else:  # CR值大于0.1, 一致性检验不通过
                print("判断矩阵的CR值为" + str(self.CR_val) + "未通过一致性检验")
                return False

    """
    算术平均法求权重
    """

    def cal_weight_by_arithmetic_method(self):
        # 求矩阵的每列的和
        col_sum = np.sum(self.array, axis=0)
        # 将判断矩阵按照列归一化
        array_normed = self.array / col_sum
        # 计算权重向量
        array_weight = np.sum(array_normed, axis=1) / self.n
        # 打印权重向量
        print("算术平均法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight

    """
    几何平均法求权重
    """

    def cal_weight_by_geometric_method(self):
        # 求矩阵的每列的积
        col_product = np.product(self.array, axis=0)
        # 将得到的积向量的每个分量进行开n次方
        array_power = np.power(col_product, 1 / self.n)
        # 将列向量归一化
        array_weight = array_power / np.sum(array_power)
        # 打印权重向量
        print("几何平均法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight

    """
    特征值法求权重
    """

    def cal_weight_by_eigenvalue_method(self):
        # 将矩阵最大特征值对应的特征向量进行归一化处理就得到了权重
        array_weight = self.max_eig_vector / np.sum(self.max_eig_vector)
        # 打印权重向量
        print("特征值法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight


if __name__ == "__main__":
    # 给出判断矩阵
    A = np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,1/2],[1/5,1/2,2,1]])
    # 初始化
    ahp = AHP(A)
    # 检测是否通过一致性检验
    if ahp.test_consist():
        # 算术平均法求权重
        weight1 = ahp.cal_weight_by_arithmetic_method()
        # 几何平均法求权重
        weight2 = ahp.cal_weight_by_geometric_method()
        # 特征值法求权重
        weight3 = ahp.cal_weight_by_eigenvalue_method()

运行结果如下：

如果给出正确的判断矩阵A

A = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]])

运行结果如下：

在上面的代码中，我们只需要更改判断矩阵A变量即可使用！

资料获取，更多粉丝福利，关注下方公众号获取

a74f7d5d03234f7c8a635562034442a0.gif#pic_center