未来属于那些相信梦想,并愿意为之付诸行动的人![]() 。
。


![]()
![]()
前言
做概率论的笔记和大家一起学习,我是看b站的这个视频梨米特.感觉讲的挺不错的,大家可以去看看,对照着我做的笔记会事半功倍。
随机实验
定义
- 实验可以在相同条件下重复进行;
- 每次实验的可能结果都不止一个,并且能事先明确实验的所有可能结果;
- 进行一次实验之前不能确定哪一个结果会出现;则称之为随机实验;简称试验E;
例如:抛掷硬币,观察正面H(head),反面T(tail)出现的情况.
样本空间
定义
样本空间:随机试验所有可能结果组成的集合,记为s或a. (sample space)
样本点:随机试验的每个结果,称为样本点,记为e. (element)
样本空间S是由全体样本点e构成的集合:s={e};
例题:
E:将-枚硬币抛掷三次,观察正面H、反面r出现的情况。
S= {H,HT,HTHTTT,TTTH,THT,THHSE:将一枚硬币抛掷三次,观察出现正面H的次数。
E:在一批灯泡中任意抽取一只,测试它的本空间的概念寿命。
S={t1t30}描述法
E,:记录某城市120急救电话台一昼夜接到的呼唤次数。
s={o,13-}={k|K∈N}
总结:求S方法!: 列举法(有限个);方法2:描述法(无限多)
随机事件
定义
随机事件:样本空间S的子集称为E的随机事件,用A, B等表示,简称事件.
事件发生:在每次试验中,当且仅当随机事件中的一个样本点出现,称此事件发生.
基本事件:由一个样本点组成的单点集,称为基本事件.
必然事件:样本空间S包含所有样本点,在每次试验中它总发生,故称为必然事件.
不可能事件:空集φ不包含任何样本点,在每次试验中都不发生,称为不可能事件.
事件间的关系、事件的运算及运算法则
回顾:随机事件是一个集合.高中我们就学过集合间的关系与运算。
引入:事件间的关系与事件的运算可按集合论中集合之间的关系和集合运算来处理,并根据“事件发生”的含义,给出它们在概率论中的含义.
事件间的关系和运算


注:(1)事件组A1,A2,....,An中任意两个事件互不相容,则称这些事件为两两互斥或两两互不相容;
(2)在一次试验中,基本事件是两两互不相容的;

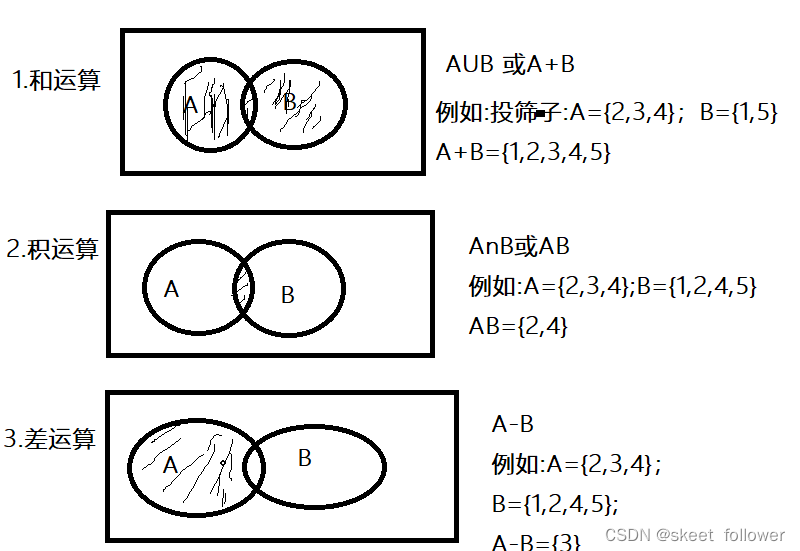
推广:n个事件A1,,A2,,,An的和事件,积事件:

事件的运算法则

注意:对偶律在平时练习中经常遇到,可以根据这句口诀背下它:" 长线变短线,开口变方向"
(1)通过事件的运算,可以将一个事件表示成与它相等的形成,便于计算
(2)事件运算顺序约定为先进行逆运算,后交运算,最后并或差运算
例题:
请写出下列随机事件.
E;:将- -枚硬币抛掷三次,观察正面H、反面T出现的情况.
A1:“第一次出现的是H", A2:“三次出现同一面”.
请写出:


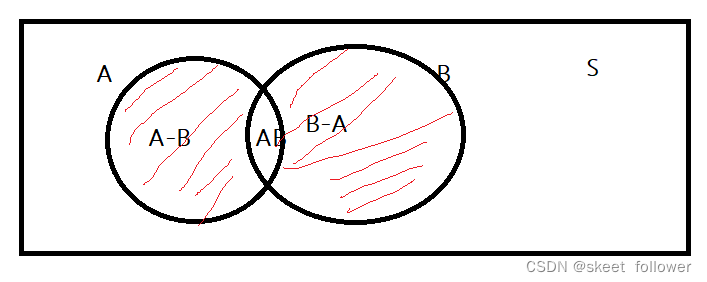
注:请借助文氏图考虑事件A-B,AB,B-A之间的关系
结论:A-B,AB,B-A两两互不相容
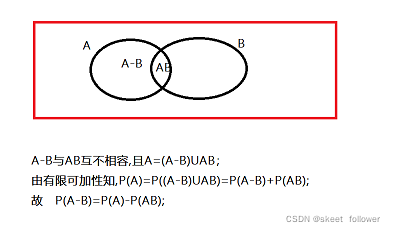
A=(A-B)UAB
B=(B-A)UAB
AUB={A-B}UABU(B-A)
频率与概率
引入:希望知道某事件在一-次试验中发生的可能性究竟有多大?即求其概率。但自从中学以来,我们还没有给“概率”-个准确的定义.
一、概率的描述性定义
定义:称随机事件A发生的可能性大小的度量(非负值)为事件A发生的概率.
二、概率的统计性定义-频率
1.定义:在相同条件下, 进行了n次试验,在这n次试验中,事件A发生的次数n,称
为事件A发生的频数,比值称为事件A发\生的频率,并记成f,(4).
2.频率的基本性质:
(1)0≤f(A)≤1;
(2) f,(S)=1;
(3)若A,A,.A,是两两互补相容的事件,
则
f(AUAU...UA)= f(A)+ f(A)...+f(4)
注:频率大小表示A发生的频繁程度.频率大,事件A发生就频繁,这就意味着事件A在- -次试验中发生的可能性大就大。
三、概率的公理化定义
1.定义:设E是随机试验,S是它的样本空间.对于E的每一个事件 A赋予-个实数,
记为P(A),如果集合函数P()满足下列条件:
(1)非负性:对每一一个事件A,有P(A)≥0;
(2)规范性:对必然事件S,有P(S)=1;
(3)可列可加性:设A,.,.,,..是两两互不相容的事件,即AA=φ, i≠j, i,j=1,2,.,..,有P(AUAU.UA,U.)= P(A)+ P(A)+...+ P(A)+...
2.概率的重要性质
性质1: P(空)=0.
性质2(有限可加性):设A,,,A,是两两互不相容的事件,即
AA,=φ, i≠j, i,j=l,2,,n,有P(A1∪A2∪.UAn)= P(A1)+ P(A2)+..+P(An)
性质3(减法公式):设A, B是任意两个事件,则P(A- B)= P(A)-P(AB).
性质4(单调性):设A,B是两个事件,若BcA,则P(A- B)=P(A)-P(B), P(A)>=P(B).
性质5(有界性):对任一事件A,有P(A)≤1.
性质6(逆事件概率):对任- -事件A,有P(A)=1-P(A).
性质7(加法公式):对于任意两个事件A.B,有P(AUB)= P(A)+ P(B)- P(AB).
推广:P(AUBUC)= P(A)+ P(B)+ P(C)一P(AB)- P(AC)- P(BC)+ P(ABC)
古典概型
中学概率知识:
加法原理:设完成一件事有n类方法(只要选择其中一类方法即可完成这件事) ,若第一
类方法有m1种,第二类方法有m2种,..第n类方法有mn,种,则完成这件事共有N=m1+m2, +..+mn,种方法.
乘法原理:设完成- -件事须有n个步骤(仅当n个步骤都完成,才能完成这件事),若第
-步有m1种方法,第二步有m2种方法, ...第n步有m,种方法,则完成这件事共有N= m1xm2x...xmn,种方法.
注:有顺序用排列,无顺序用组合
定义
若随机试验E满足:
(1)样本空间S只含有限个样本点,S={e1,e2,,,,,en};
(2) 每个基本事件(样本点)发生的可能性相同;
则称此随机试验的概率模型为等可能概型,也称为古典概型.
古典概型中,事件A={e1,e2,e3,,,,,en, }发生的概率为
p(A)=k/n=A包含的基本事件数/S中的基本事件总数。
这里没啥好说的了,就是练题练习:













几何概率
问题:若E满足:样本空间S含无限多个样本点;每个基本事件(样本点)发生的可能性相同;那么E的概率模型还是等可能概型吗?相应事件的概率又如何来求?
定义:
若随机试验E满足:
(1 )样本空间S是R"(n=1,2,3)中一个可度量的几何区域;
(2)每个样本点出现的概率相等,即样本点落入s某- -可度量的子区域A的可能性大小与A的几何度量成正比,而与A的位置及形状无关.
则事件A= {样本点落入区域A}的概率为
P(A)=A的几何度量(长度,面积,体积)/S的几何度量(长度,面积,体积)
'注: (1)古典概型:基本事件有限、等可能的随机试验;
(2)几何概型:基本事件无限、等可能的随机试验.
例题:

条件概率
引入:若已知某事件发生,如何求另一事件发生的概率?
定义:
设A,B是两个事件,且P(A)>0, 称P(B|A)=P(AB)/P(A)为在事件A发生的条件下事件B发生的条件概率。
注:要注意P(AB)与P(B|A)的区别:
P(AB)是在样本空间为S时,A, B同时发生的可能性,
P(B|A)则表示在A发生的条件下,B发生的可能性,此时样本空间已由S缩减为A.
只要在题设条件中有:“已知 A发生”或“在A发生的条件下”等,均要考虑条件概率.
性质:
例题:

乘法公式
回忆:条件概率
定理
设P(A)>0,则有P(AB)= P(A)P(B|A)上式称为乘法公式。
设P(B)>0,则有P(AB)=P(B)P(A|B)
推广:
(1)设A,B,C为事件,且P(AB)>0,则有P(ABC)= P(A)P(B|A)P(C|AB).
证明:P(ABC)=P(AB)P(C|AB)=P(A)P(B|A)P(C|AB)
(2)设A,A,,A,为n个事件,n≥2,且P(A1A2...A.n)>0,则有P(A1A2...An)= P(A1)P(A2|A1)P(A3|A1A2)-.. P(A, |A1A2--An-1.)
注: (1)注意事件发生先后次序,Ai先于Ai+1发生,可用上式.
(2)主要用来计算没有相互独立性的若干事件的积事件的概率.




全概率公式
引入:在很多实际问题中,P(A)不易直接求得,但却容易得到一-组事件,它们两两互不相容,且和事件为样本空间,并且知道相关事件概率,则此时就可以求出P(A).即:


引入:设试验E的样本空间为S,A为E的事件,B1,.,..,Bn 为S的一-个划分,且P(Bi)>0(i=l,2,,n),那么P(A)=?
定理:设实验E的样本空间位S,A为E的事件,B1,B2,,,Bn为S的一个划分,且P(Bi)>0(i=1,2,,,n),则P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+.....P(Bn)P(A|Bn)
贝叶斯公式
定理:

注:此公式先是应用条件概率公式,分母为全概率公式,是n项之和,分子是分母中的某一项,贝叶斯公式:由果导因;
全概率公式:把全概率公式中的A视为"果",把B1,B2,,,Bn视为"因",则全概率公式反应的是"由因求果"的概率问题.
例题:




独立性
回忆:条件概率

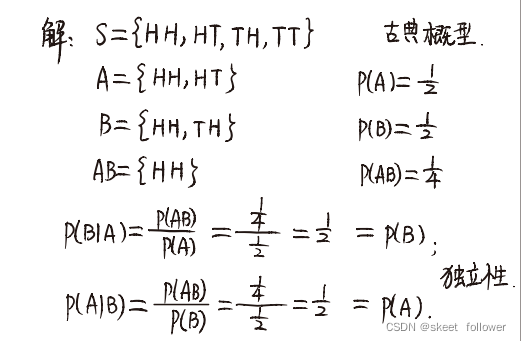
定义:
若A,B为两个事件,如果其中任何一个事件发生的概率不受另一个事件发生与否的影响,则称事件A与B相互独立.
P(B|A)=P(B);
P(A|B)=P(A);
数学定义:
设A,B为两个事件,如果P(AB)= P(A)P(B),则称事件A与B相互独立,简称A与B独立.
独立性与事件的:包含,相等,相容,对立关系不同;
注: (1)两事件相互独立与互不相容的关系.
若P(A)>0,P(B)>0则A,B独立与互不相容不能同时成立.
A,B独立>>P(AB)=P(A)P(B)>0
A,B互不相容>>AB=空,>>P(AB)=0
(2)必然事件及不可能事件与任意事件相互独立.
定理一设A,B是两事件, 且P(A)>0, 若A,B相互独立,则P(B|A)=P(B), 反之亦然.
定理二若事件A与B相互独立,则下列各对事件也相互独立: A与B,A与B,A与B.











 这篇博客详细介绍了概率论的基本概念,包括随机实验、样本空间、随机事件及其概率定义。通过实例解释了古典概型和几何概率,并探讨了条件概率、乘法公式、全概率公式和贝叶斯公式。此外,还讨论了事件的独立性及其性质,为理解概率论提供了坚实的基础。
这篇博客详细介绍了概率论的基本概念,包括随机实验、样本空间、随机事件及其概率定义。通过实例解释了古典概型和几何概率,并探讨了条件概率、乘法公式、全概率公式和贝叶斯公式。此外,还讨论了事件的独立性及其性质,为理解概率论提供了坚实的基础。







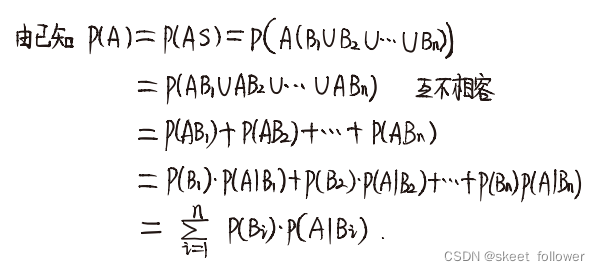






















 2852
2852

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










