【GNN】第四章 节点表征学习与节点分类任务（理论+调包实操）

本文参考自datawhale2021.6学习：图神经网络

【GNN】第一章 图论基础

【GNN】第二章 PyG中的图与图数据集

【GNN】第三章 消息传递范式与PyG的MessagePassing基类

1 图数据获取并分析

1.1 数据获取与规范化

• 节点特征归一化：NormalizeFeatures()，所有属性值相加等于1。来自PyG的transforms模块：
  torch_geometrics.transforms

from torch_geometric.datasets import Planetoid
from torch_geometric.transforms import NormalizeFeatures

# 数据集
dataset = Planetoid(root='datasets', name='Cora', 
					transform=NormalizeFeatures())

# 数据
data = dataset[0]

1.2 数据集与数据的分析

• 数据集dataset

print(f'Dataset: {dataset}:') # Cora()
print(f'Number of graphs: {len(dataset)}') # 1
print('Number of features: ',dataset.num_features) # 属性数 1433
print('Number of classes: {}'.format(dataset.num_classes)) # 分类任务数 7

• 数据data

print(data.num_nodes) # 2708
print(data.num_edges) #10556
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}') # 3.90 节点平均出/入度
print(data.train_mask.sum()) # 作为训练集的节点数 140
print(data.train_mask.sum()/data.num_nodes) # 训练节点数占总体的5%左右
print(data.contains_isolated_nodes()) # 不存在孤立点
print(data.contains_self_loops()) # 不存在自环边
print(data.is_undirected()) # 是个无向图

1.3 节点表征分布的可视化：TSNE

TSNE(n_components=2,…) sklearn.manifold.TSNE

1. t-SNE 为高维特征空间在二维/三维寻找一个投影，使得距离近的点仍近，远的仍远
2. 缺点：计算量较大，大量样本时使用Multicore-TSNE
3. 主要用于启发想法，不能基于此得到决定性的结论，因为随机种子不同会导致画出图形的不同，要通过更全面深入的研究来对想法得到确认

• 使用例子

import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklern.preprocessing import StandardScaler

# 将变量转化为数值
x = df['col'].map({
   })

# 归一化
scaler = StandardScaler() # (X-μ)/σ
x_scaled = scaler.fit_transform(x) # x可以是df、numpy

# 构建t-SNE
tsne = TSNE(random_state=随机种子) # 默认2维，随机种子使得可以重复
tsne_repr = tsne.fit_transform(x_scaled)

# 可视化t-SNE
plt.scatter(tsne_repr[:,0], tsne_repr[:,1],
			c=df['类别列，设类别为False和True'].map({
   False:'blue',True:'orange'}),
			s=点的大小, alpha=.5)

• 上述过程复杂，定义一个函数来满足接下来的随时调用
  函数参数的注释：冒号和箭头

import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

def visualize(x, color):
    tsne = TSNE(n_components=2)
    z = tsne.fit_transform(x.detach().cpu().numpy())
    # 把tensor改成numpy，color的tensor不用改
    
    plt.figure(figsize=(10,10))
    plt.xticks([])
    plt.yticks([])

    plt.scatter(z[:, 0], z[:, 1], s=70, c=color, cmap="Set2")
    plt.show()

# 调用
visualize(data.x,data.y)

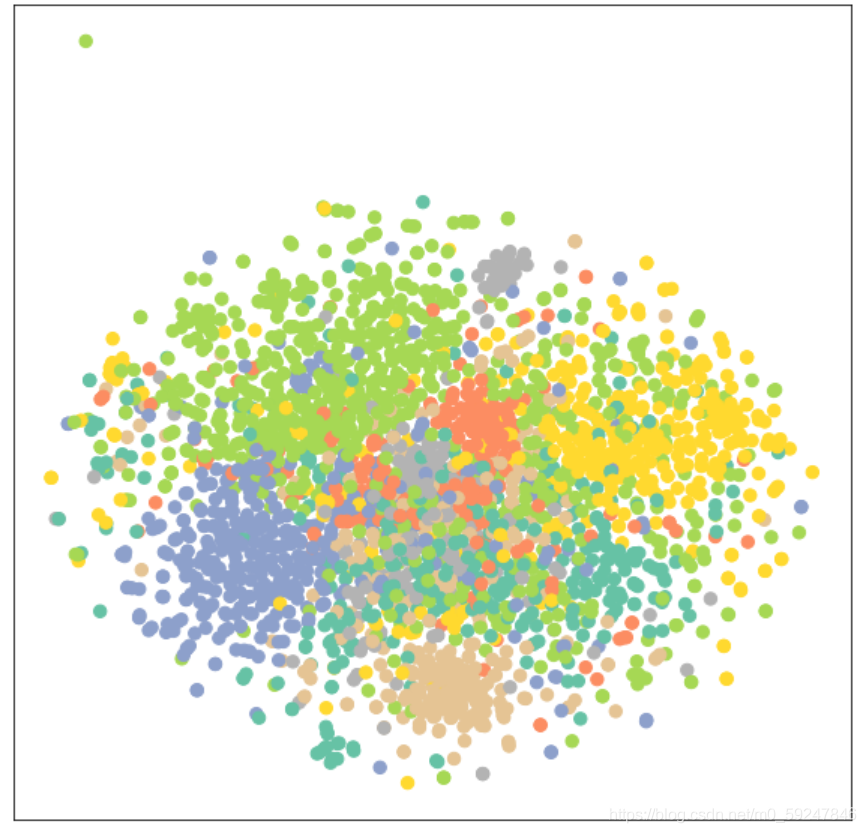
• 可见同类节点群聚的现象

2 MLP神经网络进行节点分类

2.1 复习：pytorch神经网络的构建与调用

• 构建

import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
	def __init__(self):
		super(Net,self).__init__()
		
		torch.manual_seed(1) # 设置当前cpu的种子
		# torch.cuda.manual_seed(1) # 当前gpu
		# torch.cuda.manual_seed_all() # 所有gpu
		
		self.conv1 = nn.conv2d(输入通道数,输出通道数_1,kernel,stride=1)
		self.conv2 = nn.conv2d(输出通道数_1, 输出通道数_2, kernel=(3,2),stride=1)
		self.lin1 = nn.Linear(入，出)
		self.lin2 = nn.Linear(…)
		self.lin3 = nn.Linear(…)
	
	def forward(self,x): # x是一个tensor张量，[样本数,通道,高,宽]
	
		x = self.conv1(x)
		x = F.relu(x)
		x = F.max_pool2d(x,(2,2))
		
		x = F.max_pool2d(F.relu(self.conv2(x)),2)

		x = x.view(-1, self.num_flat_features(x)) # -1这里算得是batch大小

		x = F.relu(self.lin1(x))
		x = F.relu(self.lin2(x))
		x = self.lin3(x)
		return x

	def num_flat_features(self,x):
		num_features=1
		size = x.size()[1:] # 除了batch维
		for s in size:
			num_features *= s
		return num_features
		

• 调用

net = Net()

# 参数
params = list(net.params())
len(params)  # 输出10。因为该net有5层，每层2个params，一个是网络层本身的参数，一个是该层的bias
params[0].size() # 假设输出(6,3,3,3) 这是第一个卷积层，表明其有6个卷积核（输出通道数），每个大小为3*3*3（输入通道数*卷积核大小）
params[1].size() # 在上述假设下，其输出为6，是每个卷积核的bias（输出的每个通道的bias）

# 损失函数与损失计算
criterion = nn.MSELoss()
loss = criterion(output,traget)

# 优化器创建
import torch.optim as optim
optimizer = optim.SGD(net.params(), lr=0.01)

# 权重更新
# 一次更新，一次迭代
optimizer.zero_grad() # 将所有参数的梯度缓存清零
output = net(input)
loss = criterion(output, target)
loss.backward() # 反向传播
optimizer.step() # 更新

2.2 节点分类的MLP神经网络

• 构建

import torch
import torch.nn