作者：
Linfei Pan¹, Daniel Baráth¹, Marc Pollefeys¹,², Johannes L. Schonberger²
¹ 苏黎世联邦理工学院 (ETH Zurich)
² 微软 (Microsoft)
摘要：
从图像中恢复三维结构和相机运动一直是计算机视觉研究的长期焦点，被称为运动恢复结构（Structure-from-Motion, SfM）。该问题的解决方案分为增量式（incremental）和全局式（global）两种方法。迄今为止，由于其卓越的精度和鲁棒性，最流行的系统遵循增量范式，而全局方法则在可扩展性和效率上具有显著优势。本文中，我们重新审视全局SfM问题，提出了GLOMAP作为一个新的通用系统，其性能优于最先进的全局SfM方法。在精度和鲁棒性方面，我们取得了与最广泛使用的增量式SfM系统COLMAP相当或更优的结果，同时速度快了几个数量级。我们在 https://github.com/colmap/glomap 上开源分享了我们的系统实现。
1 引言
从图像集合中恢复三维结构和相机运动仍然是计算机视觉的一个基本问题，对于各种下游任务（如新视角合成[38,50]或基于云的地图构建与定位[39,58]）高度相关。文献中通常将此问题称为运动恢复结构（SfM）[75]，多年来，解决该问题出现了两种主要范式：增量式和全局式方法。两者都始于基于图像的特征提取和匹配，然后进行两视图几何估计，以构建输入图像的初始视图图（view graph）。增量式方法随后从两个视图开始“播种”重建，并通过顺序注册额外的相机图像及其相关的三维结构来扩展它。这个顺序过程交织着绝对相机位姿估计、三角测量（triangulation）和捆集调整（bundle adjustment）。尽管能达到高精度和鲁棒性，但由于代价高昂的重复捆集调整，限制了其可扩展性。相比之下，全局方法通过独立的旋转平均（rotation averaging）和平移平均（translation averaging）步骤，一次性恢复所有输入图像的相机几何，共同考虑视图图中的所有两视图几何关系。通常，全局估计的相机几何随后被用作三维结构三角测量的初始化，接着是最终的全局捆集调整步骤。虽然最先进的增量方法被认为更精确和鲁棒，但全局方法的重建过程更具可扩展性，并且在实践中快了几个数量级。
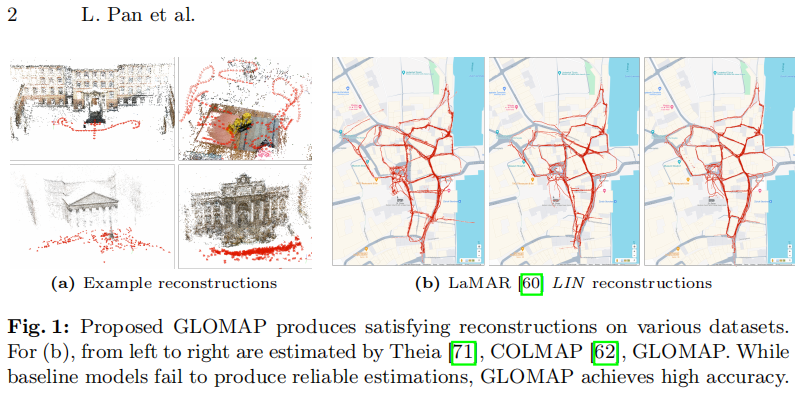
在本文中，我们重新审视全局SfM问题，提出了一个全面的系统，在达到与最先进增量式SfM（例如图1a）相当的精度和鲁棒性的同时，保持了全局方法的效率和可扩展性。
增量式与全局式SfM之间精度和鲁棒性差距的主要原因在于全局平移平均步骤。平移平均描述的是在通过旋转平均恢复相机朝向（orientations）之后，根据视图图中的相对位姿集合估计全局相机位置（positions）的问题。在实践中，这个过程面临三大挑战：
- 尺度模糊性：估计的两视图几何中的相对平移只能确定到尺度[27]。因此，为了准确估计全局相机位置，需要相对方向的三元组（triplets）。然而，当这些三元组形成倾斜三角形时，估计的尺度特别容易受到观测噪声的影响[47]。
- 内在参数依赖：将相对两视图几何精确分解为旋转和平移分量需要已知精确的相机内在参数（intrinsics）。没有这些信息，估计的平移方向通常存在较大误差。
- 共线运动退化：近似共线的运动会导致重建问题退化（degenerate）。这种运动模式很常见，尤其是在序列数据集中。
这些问题共同导致了相机位置估计的不稳定性，严重影响了现有全局SfM系统的整体精度和鲁棒性。受平移平均困难的启发，大量研究工作致力于此问题。许多近期方法[5,10,17-19,32,79]与增量式SfM有一个共同特点：它们将图像点纳入问题公式中。基于此见解，我们提出一个全局SfM系统，直接在单个全局定位（global positioning）步骤中结合相机位置和三维结构的估计。
本文的主要贡献是引入了一个通用的全局SfM系统，称为GLOMAP。与先前全局SfM系统的核心区别在于全局定位步骤。我们的方法不是先执行不适定（ill-posed）的平移平均，然后再进行全局三角测量，而是执行相机和点位置的联合估计。GLOMAP在鲁棒性和精度上达到了与最先进的增量式SfM系统[62]相当的水平，同时保持了全局SfM流程的效率。与大多数先前的全局SfM系统不同，我们的系统能够处理未知相机内在参数（例如来自互联网照片），并能鲁棒地处理序列图像数据（例如手持视频或自动驾驶场景）。我们在 https://github.com/colmap/glomap 上开源分享了我们的系统实现。
2 全局运动恢复结构综述
全局SfM流程通常包含三个主要步骤：对应搜索、相机位姿估计以及相机与结构联合优化。接下来几节详细回顾了最先进的算法和框架。
2.1 对应搜索
增量式和全局式SfM都从输入图像集合
I={I1,⋯ ,IN} 的显著图像特征提取开始。传统上，首先检测特征点[21,44]，然后利用检测点周围局部上下文导出的紧凑签名（signature）进行描述。接着是搜索图像对(I_i, I_j)之间的特征对应关系，这始于高效识别具有重叠视场的图像子集[4]，然后通过成本更高的过程[44,59]进行匹配。匹配通常首先纯粹基于紧凑的视觉签名完成，最初会产生相对大量的外点（outliers）。然后通过鲁棒地[8]恢复重叠图像对的两视图几何来验证这些对应点。根据相机的几何配置，对于具有一般运动或纯相机旋转（pure camera rotation）的平面场景，会产生单应矩阵 HijH_{ij}Hij；对于具有一般运动的一般场景，会产生基础矩阵 FijF_{ij}Fij（未标定）或本质矩阵 EijE_{ij}Eij（已标定）。当相机内在参数大致已知时，这些矩阵可以分解[27]为相对旋转 Rij∈SO(3)和平移 tij∈R3。
计算出的两视图几何及其关联的内点对应关系定义了视图图 G，它作为全局重建步骤的输入。在我们的流程中，我们依赖COLMAP[62]的对应搜索实现[61]，使用RootSIFT特征和可扩展的词袋（bag-of-words）图像检索[63]来查找用于暴力特征匹配的候选重叠图像对。
2.2 全局相机位姿估计
全局相机位姿估计是区分全局式与增量式SfM的关键步骤。全局SfM不是通过重复的三角测量和捆集调整来顺序注册相机，而是旨在一次性估计所有相机位姿 Pi=(Ri,ci)∈SE(3)，将视图图 G作为输入。为了使问题易于处理，通常将其分解为独立的旋转平均和平移平均步骤[53,71]，一些工作还在之前[72]对视图图进行优化，或直接从两视图几何的视图图中估计相机位姿[35,36]。主要挑战在于通过仔细建模和解决优化问题来处理视图图中的噪声和外点。
旋转平均（Rotation Averaging），有时也称为旋转同步（rotation synchronization），已被研究数十年[26,49]，并与位姿图优化（PGO）算法[12,13]相关。它通常被表述为一个非线性优化问题，惩罚全局旋转与估计的相对位姿之间的偏差。具体来说，绝对旋转 RiR_{i}Ri 和相对旋转 RijR_{i j}Rij 理想情况下应满足约束 Rij=RjRi⊤R_{i j}=R_{j} R_{i}^{\top}Rij=RjRi⊤。然而，由于噪声和外点，这在实践中并不精确成立。因此，该问题通常建模为一个鲁棒的最小度量目标函数并进行优化：
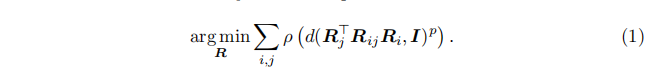
Hartley等人[26]全面综述了鲁棒函数 ρ（例如Huber）、旋转参数化（例如四元数或轴角）和距离度量 d（例如弦距离或测地线距离）的各种选择。
基于这些原理，已经提出了多种方法。Govindu[24]通过四元数将问题线性化，而Martinec和Pajdla[49]通过省略旋转矩阵的某些约束来松弛问题。Eriksson等人[22]利用了强对偶性。Wilson等人[78]研究了该问题的易处理条件。采用基于半定规划（SDP）松弛[5,23]的方法通过最小化弦距离[26]来确保最优性保证。Dellaert等人[20]将问题顺序提升到 SO(n)SO(n)SO(n) 内的更高维旋转中，以避免标准数值优化技术可能陷入的局部极小值[40,48]。各种鲁棒损失函数被探索用于处理外点[14,15,25,68,82]。最近，基于学习的方法开始出现。NeuRoRa[57]、MSP[81]和PoGO-Net[41]利用图神经网络（GNN）来剔除外点并估计绝对相机位姿。DMF-synch[73]依赖于矩阵分解技术进行位姿提取。在本工作中，我们使用Chatterjee等人[14]方法的自实现，作为一种在存在噪声和外点污染的输入旋转下提供准确结果的可扩展方法。
平移平均（Translation Averaging）。旋转平均之后，旋转 RiR_{i}Ri 可以从相机位姿中分离出来。剩下需要确定的是相机位置 cic_{i}ci。平移平均描述的是估计全局相机位置的问题，这些位置与基于约束
的成对相对平移 tij 最大程度一致。然而，由于噪声、外点以及相对平移的未知尺度，这项任务尤其具有挑战性。原则上，如果视图图具有平行刚性（parallel rigidity）属性，则可以唯一确定相机位姿。平行刚性，也称为方位刚性（bearing rigidity），在计算机视觉[7,56]、机器人学[37]、决策与控制[84]以及计算机辅助设计[67]等领域都有研究。Arrigoni等人[6]对该主题进行了统一综述。
过去几年提出了不同的平移平均方法。Govindu的开创性工作[24]最小化了相对相机位置与观测方向之间的叉积。Jiang等人[34]在三元组单元上线性化问题。Wilson等人[79]直接优化方向差异并设计了一个专用的外点过滤机制。Ozyesil等人[55]提出了原始问题的凸松弛，并用 L1L_{1}L1 损失解决鲁棒的最小未平方偏差（LUD）问题。Zhuang等人[85]意识到LUD方法在相机基线方面的敏感性，并提出了用于优化的基于双线性角度（Bilinear Angle-based Translation Averaging, BATA）的误差。尽管这些工作取得了显著改进，但平移平均通常仅在视图图连接良好时可靠工作。当相机经历或接近共线运动时，该问题本质上是病态的，并且对噪声测量敏感。此外，只有在已知相机内在参数的情况下，才可能从两视图几何中提取相对平移。当此类信息不准确时，提取的平移不可靠。受观察到点轨迹（point tracks）通常有助于平移平均[5,17-19,32,79]的启发，在我们提出的系统中，我们跳过了平移平均步骤。相反，我们直接执行相机和点位置的联合估计。我们将此步骤称为全局定位（global positioning），详情在第3.2节介绍。
用于相机位姿估计的结构。一些工作探索了将三维结构纳入相机位置估计。Ariel等人[5]直接使用两视图几何中的对应点来估计全局平移。Wilson等人[79]发现三维点可以类似于相机中心的方式处理，因此可以轻松地融入优化。Cui等人[18]通过包含具有线性关系的点轨迹扩展了[34]。为了减少尺度漂移（scale drifting），Holynski等人[32]将线和面特征整合到优化问题中。Manam等人[46]通过重新加权优化中的相对平移来纳入对应点。LiGT[10]提出了一种“仅位姿”（pose only）的方法，利用点施加的线性全局平移约束来解决相机位置。这些工作的共同主题是，纳入三维场景结构的约束有助于提高相机位置估计的鲁棒性和准确性，这为我们提供了灵感。
2.3 全局结构与位姿优化
在恢复相机位姿之后，可以通过三角测量获得全局三维结构。结合相机外参和内在参数，三维结构通常通过全局捆集调整进行优化。
全局三角测量。给定两视图匹配，可以利用传递性对应点来提高完整性和准确性[62]。Moulon等人[52]提出了一种高效连接轨迹（tracks）的方法。多视图点的三角测量有着悠久的研究历史[29,45]。此类任务的常见做法是直接线性变换（DLT）和中点法[2,27,29]。最近，LOST[31]被提出作为一种基于不确定性的三角测量方法。然而，上述三角测量机制在面对任意水平的外点时常常失效。在这方面，Schonberger等人[62]提出了一种基于RANSAC的三角测量方案，旨在存在误匹配的情况下建立多点轨迹。相反，我们的方法通过单一的、与相机位置联合的全局优化方法直接估计三维点（见第3.2节）。
全局捆集调整对于获得精确的最终三维结构 Xk∈R3、相机外参 Pi 和相机内在参数 πi 至关重要。它被表述为一个联合鲁棒优化问题，通过最小化重投影误差实现：
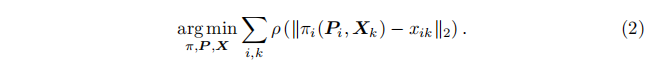
关于捆集调整的全面综述，请参阅Triggs等人[74]。
2.4 混合式运动恢复结构
为了结合增量式SfM的鲁棒性和全局式SfM的效率，先前的工作制定了混合系统。HSfM[17]提出增量式地估计相机位置（伴随旋转）。Liu等人[43]提出了一种图划分方法，首先将整个图像集划分为重叠的簇（clusters）。在每个簇内，通过全局SfM方法估计相机位姿。然而，根据其公式，当相机内在参数不准确时，此类方法仍然不适用。我们的方法通过对全局定位步骤中目标函数的不同建模克服了这一限制。
2.5 运动恢复结构框架
有多个开源的SfM流程可用。
- 增量式SfM：由于其在实际场景中的鲁棒性和准确性，增量式SfM范式是目前使用最广泛的。Bundler[69]和VisualSfM[80]是十年前的系统。在此基础上，Schnberger等人[62]开发了COLMAP，这是一个通用的SfM和多视图立体（MVS）[64]系统。COLMAP功能多样，并在许多数据集上展现出强大的性能，使其成为近年来基于图像的3D重建的标准工具。
- 全局式SfM：也有几个开源的全局SfM流程。OpenMVG[53]是此类别的杰出框架。它从几何验证的匹配开始，使用a contrario RANSAC[51]估计相对位姿。接着，OpenMVG通过调整环长（cycle length）权重评估旋转一致性以剔除外点边，并使用稀疏特征值求解器利用剩余的边求解全局旋转。全局平移通过三焦张量（trifocal tensor）进行优化，然后使用 L∞ 方法进行平移平均。最后，OpenMVG通过逐点优化和全局捆集调整执行全局三角测量。
Theia[71]是另一个成熟的全局SfM流程。它采用与OpenMVG类似的方法：首先通过平均估计全局旋转，然后通过平移平均估计相机位置。对于旋转平均，Theia采用了[14]中的鲁棒方案。对于平移平均，它默认使用LUD方法[55]。该流程以与OpenMVG类似的全局三角测量和捆集调整结束。
- 基于学习的流程：有几个基于学习的流程可用。PixSfM[42]提出了一种联合优化特征和结构的机制，以实现亚像素级精确重建，并且可以与我们的系统结合使用。VGG SfM[76]提出了一个用于SfM任务的端到端学习框架，而Zhuang等人[83]提出直接在像素级对应点上操作以回归相机位置。然而，这两种方法仅限于处理数十张图像。
在本文中，我们提出了一个新的端到端全局SfM流程，并将其作为开源贡献发布给社区，以促进下游应用和进一步研究。
3 技术贡献
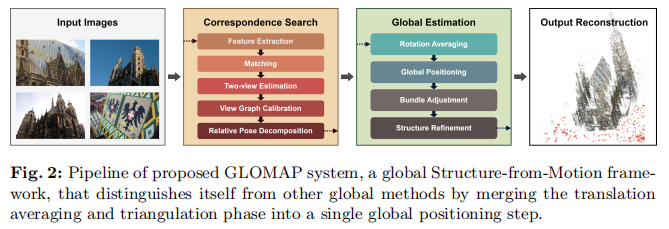
本节介绍我们的关键技术贡献，旨在改进最先进的全局SfM（参见图2），并在鲁棒性和精度上缩小与增量式SfM的差距。
3.1 特征轨迹构建
为了获得准确的重建，必须仔细构建特征轨迹（feature tracks）。我们首先仅考虑由两视图几何验证产生的内点特征对应关系。在此步骤中，我们区分两视图几何的初始分类[62]：如果单应矩阵 HHH 最能描述两视图几何，则使用 HHH 进行内点验证。同样的原则适用于本质矩阵 EEE 和基础矩阵 FFF。我们通过执行手性检验（cheirality test）[28,77]进一步过滤外点。接近任何极点（epipole）或具有小三角测量角度的匹配也会被移除，以避免由于大不确定性导致的奇异性。在成对过滤所有视图图边之后，我们通过连接所有剩余的匹配点来形成特征轨迹。
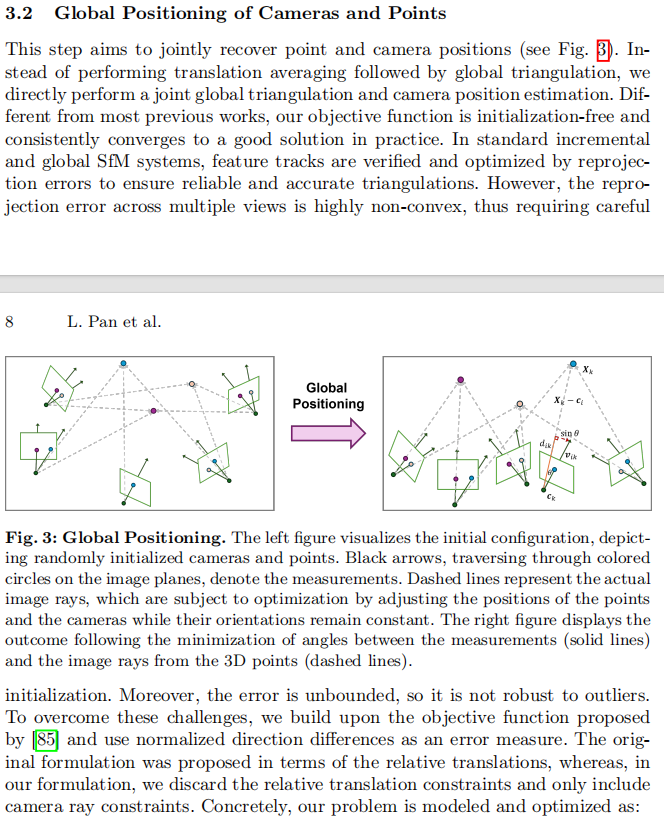
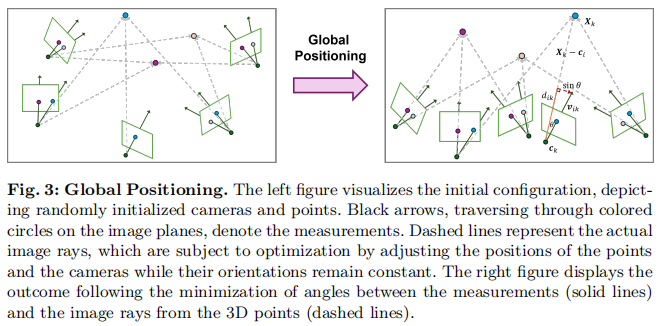
3.2 相机与点的全局定位
此步骤旨在联合恢复点和相机位置（见图3）。我们不执行平移平均后再进行全局三角测量，而是直接执行联合全局三角测量和相机位置估计。与大多数先前工作不同，我们的目标函数无需初始化，并且在实践中始终收敛到良好的解。在标准的增量式和全局式SfM系统中，特征轨迹通过重投影误差进行验证和优化，以确保可靠和精确的三角测量。然而，多视图的重投影误差是高度非凸的，因此需要仔细的初始化。此外，该误差是无界的，因此对外点不鲁棒。为了克服这些挑战，我们基于[85]提出的目标函数，并使用归一化的方向差异（normalized direction differences）作为误差度量。原始公式是针对相对平移提出的，而在我们的公式中，我们丢弃了相对平移约束，仅包含相机光线约束（camera ray constraints）。具体来说，我们的问题被建模并优化为：
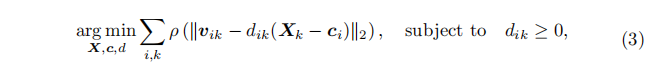
其中 vik 是从相机 ci 观察点 Xk 的全局旋转后的相机光线（globally rotated camera ray），而 dik 是一个归一化因子。我们使用Huber[33]作为鲁棒函数 ρ，并使用来自Ceres[3]的Levenberg-Marquardt[40]作为优化器。所有点和相机变量通过在范围 [−1,1]内的均匀随机分布进行初始化，而归一化因子则初始化为 dik=1。我们将涉及未知内在参数相机的项的权重降低2倍，以减少它们的影响。
与重投影误差相比，这有几个优点：
- 收敛性：正如我们实验所展示的，由于其双线性形式[85]，该目标函数在随机初始化下能够可靠地收敛。
与经典的平移平均相比，在优化中丢弃相对平移项有两个关键优势：
- 对未知/不准确内在参数的适用性：我们的方法适用于相机内在参数不准确或未知的数据集，以及不遵循预期针孔模型的退化相机（例如处理任意互联网照片时）。这是因为求解相对平移需要精确的内在参数知识。当内在参数偏离预期值时，估计的两视图平移存在较大误差。由于未知尺度导致的平移平均本身是不适定的，从噪声和外点污染的观测中恢复相机位置具有挑战性，特别是当相对平移误差随着基线变长而加剧时。我们提出的流程转而依赖于对两视图几何的仔细过滤，并且误差是相对于相机光线定义的。因此，差的相机内在参数只会偏向于单个相机的估计，而不会同时偏向其他重叠的相机。
- 对共线运动场景的适用性：这是平移平均的一个已知退化情况。与成对相对平移相比，特征轨迹约束了多个重叠的相机。因此，我们提出的流程在常见的向前或侧向运动场景中（见第4.3节）能更可靠地工作。
3.3 全局捆集调整
全局定位步骤为相机和点提供了鲁棒的估计。然而，精度有限，尤其是在相机内在参数事先未知的情况下。作为进一步的优化，我们使用Levenberg-Marquardt和Huber损失作为鲁棒函数执行几轮全局捆集调整。在每一轮中，相机旋转首先固定，然后与内在参数和点一起进行联合优化。这种设计对于重建序列数据尤为重要。在构建第一个捆集调整问题之前，我们基于角度误差对3D点观测进行预过滤，同时对未标定相机允许更大的误差。之后，我们基于图像空间中的重投影误差过滤轨迹。当过滤轨迹的比率低于0.1%时，迭代停止。
3.4 相机聚类
对于来自互联网的图像，非重叠的图像可能会被错误地匹配在一起。因此，不同的重建会坍缩成一个。为了克服这个问题，我们通过对相机进行聚类（clustering）来进行后处理重建。首先，通过计算每对图像间可见点的数量来构建共视图（covisibility graph）GGG。计数少于5的点对将被丢弃，因为低于这个数量无法可靠确定相对位姿，并使用剩余点对的中位数来设置内点阈值 τ\tauτ。然后，我们通过在 GGG 中寻找强连通分量（strongly connected components）来找到约束良好的相机簇。这样的分量定义为仅连接计数大于 τ\tauτ 的点对。之后，我们谨慎尝试合并两个强分量，如果它们之间至少有两条边计数大于0.75τ\tauτ。我们递归地重复此过程，直到没有更多的簇可以合并。每个连通分量作为一个独立的重建输出。
3.5 提出的流程
提出的方法流程总结在图2中。它包含两个主要组件：对应搜索和全局估计。
- 对应搜索：从特征提取和匹配开始。估计两视图几何（包括基础矩阵、本质矩阵和单应矩阵）。几何上不可能的匹配被排除。然后，在几何验证的图像对上执行类似于Sweeney等人[72]的视图图标定（view graph calibration）。使用更新后的相机内在参数，估计相对相机位姿。
- 全局估计：通过平均[14]估计全局旋转，并通过阈值化 RijR_{ij}Rij 和 RjRi⊤R_j R_i^\topRjRi⊤ 之间的角度距离来过滤不一致的相对位姿。然后，通过全局定位联合估计相机和点的位置，接着进行全局捆集调整。可选地，可以通过结构优化（structure refinement）进一步提升重建精度。在此步骤中，使用估计的相机位姿对点进行重新三角测量（retriangulation），并执行几轮全局捆集调整。也可以应用相机聚类来获得连贯的重建。
4 实验
为了展示我们提出的GLOMAP系统的性能，我们在各种数据集上进行了广泛的实验，范围从已标定到未标定，以及从无序到序列场景。更具体地说，我们在ETH3D[65,66]、LaMAR[60]、2023图像匹配挑战赛（IMC 2023）[16]和MIP360[9]数据集上，与最先进的框架（OpenMVG[53]、Theia[71]、COLMAP[62]）进行了比较。此外，我们进行了消融实验以研究所提系统不同组件的行为。
评估指标：
在所有评估中，我们采用两个标准指标：
- 无序图像数据：我们报告曲线下面积（AUC, Area Under the recall Curve）分数，该分数根据每对图像之间最大相对旋转和相对平移误差计算得出，类似于[16,30,65]。这种误差公式考虑了所有可能的相机对之间的偏差。
- 序列图像数据：我们报告根据相机位置误差计算的AUC分数，该误差在使用鲁棒RANSAC方案[62]将重建结果全局对齐到地面真值（ground truth）后得出。当图像以序列方式拍摄时，尤其是在相机接近共线的情况下，相对误差不能很好地捕捉尺度漂移（scale drift）。因此，我们直接关注相机位置。
为了公平比较，我们使用相同的特征匹配作为所有方法的输入，因此也将对应搜索排除在报告的运行时间之外。我们也尝试使用OpenMVG和Theia的对应搜索实现，但一致发现使用COLMAP获得的结果更好。我们使用Kapture[1]将验证的匹配导入到OpenMVG。我们对GLOMAP使用固定设置，对OpenMVG和Theia使用默认推荐设置。
4.1 已标定图像集合
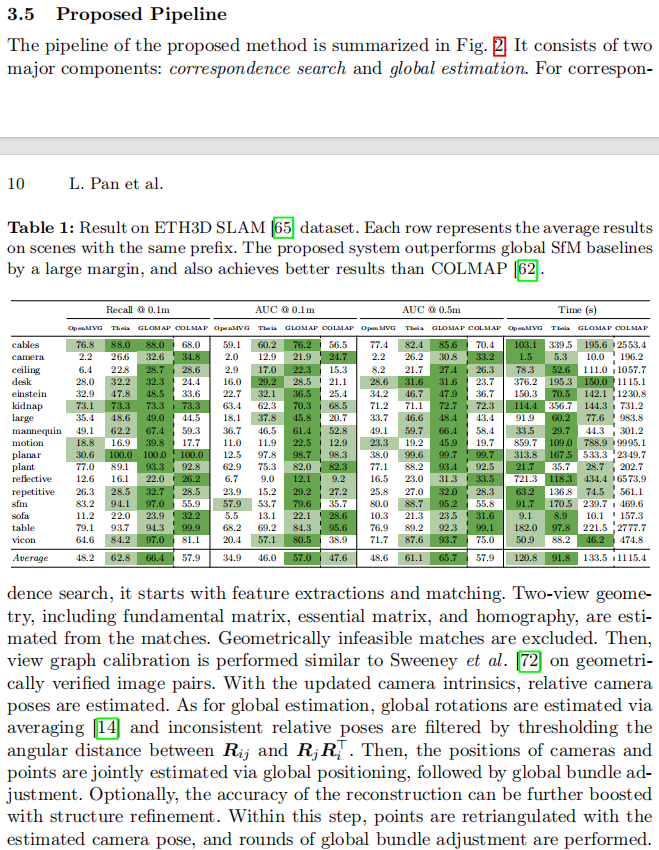
- ETH3D SLAM[65]：这是一个具有挑战性的数据集，包含稀疏特征、动态物体和剧烈光照变化的序列数据。我们在带有毫米级精度地面真值的训练序列上评估了我们的方法。测试序列和某些帧没有地面真值，因此我们不考虑它们。结果如表1所示。表中的每一行对共享相同前缀的序列结果进行平均（完整结果见补充材料）。结果表明，我们提出的GLOMAP系统在0.1m和0.5m阈值下的AUC分别比COLMAP高出约9分和8分，同时召回率高出约8%，且速度比COLMAP快一个数量级。与其他全局SfM流程相比，GLOMAP在召回率上分别高出18%和4%，在0.1m AUC上高出约11分，证实了其鲁棒性。
- ETH3D MVS(rig)[66]：每个场景包含约1000次多相机阵列曝光，每次曝光包含4张图像。该数据集包含室内外场景，5个训练序列具有毫米级精度地面真值。我们没有固定任何方法的阵列位姿。结果见表2。我们的方法成功重建了所有场景。相比之下，OpenMVG在所有场景上表现不佳，COLMAP在一个场景上失败，Theia的表现则始终比我们差。在COLMAP成功的序列上，我们取得了相似或更高的精度。我们的运行时间略慢于全局SfM基线，但比COLMAP快约3.5倍。
- ETH3D MVS(DSLR)[66]：包含无序的高分辨率室内外场景图像，训练和测试序列均具有毫米级精度地面真值，结果见表3。与其他ETH3D数据集一致，我们的方法优于OpenMVG和Theia，同时达到与COLMAP相当的精度。对于
exhibition_hall，由于场景的旋转对称性导致旋转平均坍缩，GLOMAP表现不准确。由于场景规模较小，所有方法的运行时间相当。
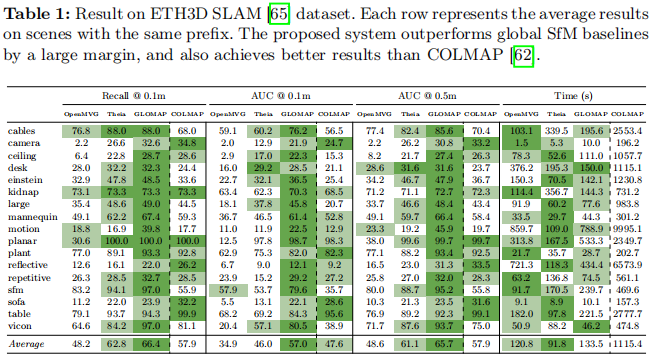
表1：ETH3D SLAM[65]数据集上的结果。每行代表具有相同前缀的场景的平均结果。提出的系统大幅优于全局SfM基线，并且也比COLMAP[62]取得更好结果。
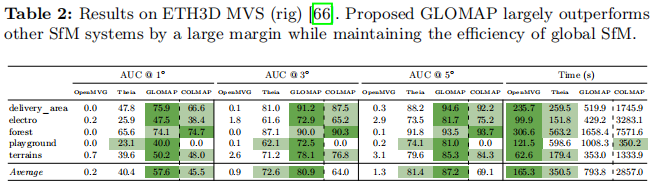
表2：ETH3D MVS(rig)[66]上的结果。提出的GLOMAP大幅优于其他SfM系统，同时保持了全局SfM的效率。
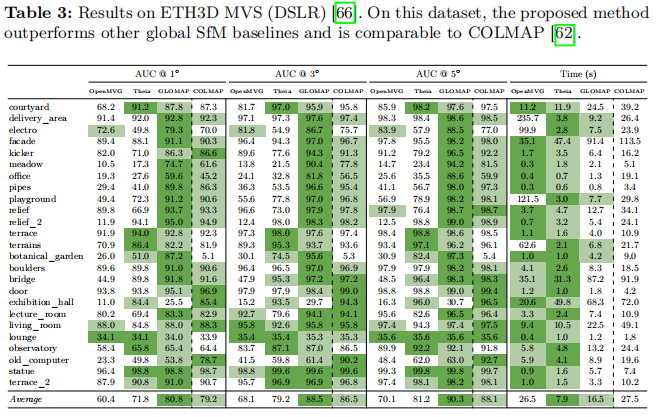
表3：ETH3D MVS(DSLR)[66]上的结果。在此数据集上，提出的方法优于其他全局SfM基线，并与COLMAP[62]相当。
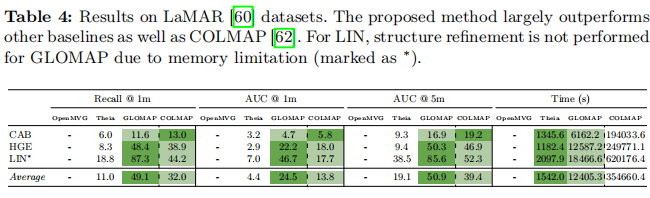
表4：LaMAR[60]数据集上的结果。提出的方法大幅优于其他基线以及COLMAP[62]。对于LIN，由于内存限制（标记为），GLOMAP未执行结构优化。
4.2 未标定图像集合
- IMC 2023[16]：包含复杂场景上的无序图像集合。图像来源多样，通常缺乏先验相机内在参数。该数据集的地面真值由COLMAP[62]构建（使用保留图像）。由于该数据集的准确性不是很高，我们遵循He等人[30]的方案，在 3∘,5∘,10∘ 阈值下报告AUC分数。训练集上的结果见表5。在此数据集上，所提方法在 3∘,5∘和 10∘ 的平均AUC分数比其他全局SfM基线高出数倍。运行时间与其他全局SfM流程相似。与COLMAP[62]相比，所提方法在 3∘,5∘和 10∘ 的AUC分数高出约4分，并且快约8倍。
- MIP360[9]：包含7个以物体为中心的场景，由同一相机拍摄的高分辨率图像。提供的COLMAP模型被视为该数据集的（伪）地面真值。类似地，由于地面真值精度有限，报告了在3°,5°,和10°下的AUC分数。COLMAP重建使用与其他方法相同的匹配重新估计。结果总结在表6中，我们的方法比其它全局SfM方法显著更接近参考模型，而重新运行COLMAP产生的结果与我们相似。我们比COLMAP快1.5倍以上。
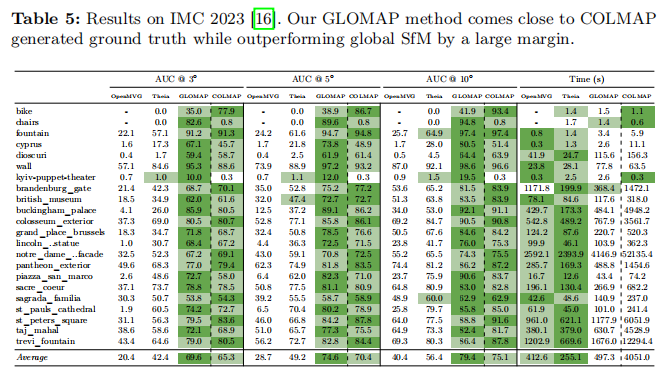
表5：IMC 2023[16]上的结果。我们的GLOMAP方法接近COLMAP生成的地面真值，同时大幅优于全局SfM。
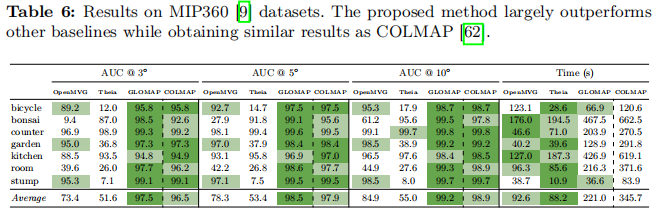
表6：MIP360[9]数据集上的结果。提出的方法大幅优于其他基线，同时获得了与COLMAP[62]相似的结果。
4.3 消融实验
为了证明全局定位策略的有效性，我们进行了实验，通过以下方式替换该组件：
- 仅添加相对平移约束（记为
BATA, cam） - 同时添加点和平移约束（记为
BATA, cam+pt）。
对于BATA, cam+pt实验，我们对两种约束使用了与Theia的LUD[55]实现类似的加权策略。对于BATA, cam和LUD实验，我们执行额外的全局定位（相机固定）以获得点位置用于后续捆集调整。我们在ETH3D MVS(DSLR)[66]和IMC 2023[9]上进行了测试。结果总结在表7中。我们看到相对平移约束会恶化收敛性和整体性能。
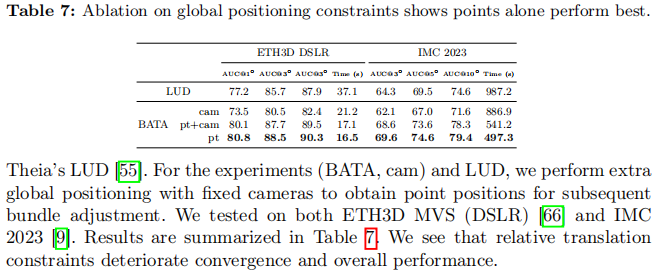
表7：全局定位约束消融实验表明仅使用点约束（pt）效果最佳。
4.4 局限性
虽然通常能取得令人满意的性能，但仍然存在一些失败案例。主要原因在于旋转平均的失败，例如由于对称结构（见表3中的 Exhibition_Hall）。在这种情况下，我们的方法可以与现有方法（如Doppelganger[11]）结合使用。此外，由于我们依赖于传统的对应搜索，错误估计的两视图几何或完全无法匹配图像对（例如由于剧烈的外观或视角变化）将导致结果质量下降，或在最坏情况下导致灾难性失败。
5 结论
总之，我们提出了GLOMAP作为一个新的全局SfM流程。该类别的先前系统被认为效率更高但不如增量方法鲁棒。我们重新审视了这个问题，得出结论：关键在于在优化中使用点约束。我们没有通过不适定的平移平均来估计相机位置，再通过点三角测量单独获得三维结构，而是将它们合并为一个单一的全局定位步骤。在各种数据集上的广泛实验表明，所提出的系统在精度和鲁棒性方面达到或优于增量方法，同时速度快了几个数量级。该代码以商业友好许可证开源提供。
扫一扫
755
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
