【SVM时序预测】基于支持向量机的时间序列预测(libsvm)附matlab代码

 ✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知,完整Matlab代码及仿真咨询内容私信。

🌿 往期回顾可以关注主页，点击搜索

⛄ 内容介绍

基于支持向量机(SVM)的时间序列测可以使用libsvm库来实现。libsvm是一个用于支持向量机的开源软件库，提供了一系列用于训练和预测的函数。

下面是基于libsvm实现时间序列预测的一般步骤：

1. 数据准备：准备用于训练和测试的时间序列数据。确保数据包含输入特征和对应的目标输出。
2. 特征工程：对时间序列数据进行特征工程，将其转换为机器学习算法可以处理的特征向量。常用的方法包括滑动窗口法、差分法等。
3. 数据划分：将时间序列数据划分为训练集和测试集。通常，训练集用于训练模型，测试集用于评估模型的性能。
4. 模型训练：使用libsvm库中的函数来训练SVM模型。在训练过程中，需要设置SVM模型的参数，如核函数类型、惩罚项系数等。
5. 模型预测：使用训练好的SVM模型对测试集进行预测。将测试集的特征向量输入到模型中，可以得到对应的预测结果。
6. 评估性能：使用适当的性能指标(如均方根误差、平均绝对误差等)来评估模型的预测效果。
7. 参数调优：根据模型的性能评估结果，可以调整SVM模型的参数，如核函数参数、惩罚项系数等，以提高预测性能。

⛄ 代码

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  导入数据(时间序列的单列数据)
result = xlsread('数据集.xlsx');

%%  数据分析
num_samples = length(result);  % 样本个数 
kim = 15;                      % 延时步长(kim个历史数据作为自变量)
zim =  1;                      % 跨zim个时间点进行预测

%%  构造数据集
for i = 1: num_samples - kim - zim + 1
    res(i, :) = [reshape(result(i: i + kim - 1), 1, kim), result(i + kim + zim - 1)];
end

%%  划分训练集和测试集
temp = 1: 1: 922;

P_train = res(temp(1: 700), 1: 15)';
T_train = res(temp(1: 700), 16)';
M = size(P_train, 2);

P_test = res(temp(701: end), 1: 15)';
T_test = res(temp(701: end), 16)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

%%  创建模型
c = 4.0;    % 惩罚因子
g = 0.8;    % 径向基函数参数
cmd = [' -t 2',' -c ',num2str(c),' -g ',num2str(g),' -s 3 -p 0.01'];
model = svmtrain(t_train, p_train, cmd);

%%  仿真预测
[t_sim1, error_1] = svmpredict(t_train, p_train, model);
[t_sim2, error_2] = svmpredict(t_test , p_test , model);

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);

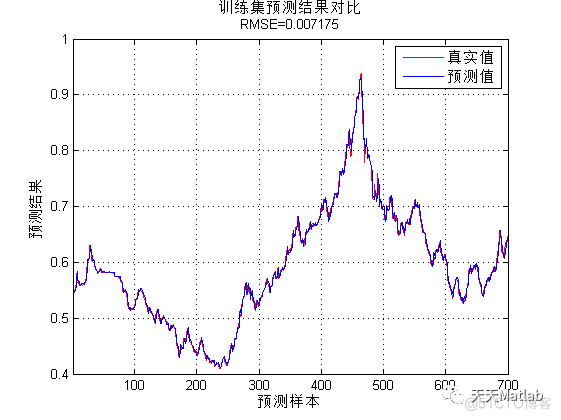
%%  绘图
figure
plot(1: M, T_train, 'r-', 1: M, T_sim1, 'b-', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
grid

figure
plot(1: N, T_test, 'r-', 1: N, T_sim2, 'b-', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])
grid

%%  相关指标计算
% R2
R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test  - T_sim2')^2 / norm(T_test  - mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

% MAE
mae1 = sum(abs(T_sim1' - T_train)) ./ M ;
mae2 = sum(abs(T_sim2' - T_test )) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

% MBE
mbe1 = sum(T_sim1' - T_train) ./ M ;
mbe2 = sum(T_sim2' - T_test ) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])

%%  绘制散点图
sz = 25;
c = 'b';

figure
scatter(T_train, T_sim1, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('训练集真实值');
ylabel('训练集预测值');
xlim([min(T_train) max(T_train)])
ylim([min(T_sim1) max(T_sim1)])
title('训练集预测值 vs. 训练集真实值')

figure
scatter(T_test, T_sim2, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('测试集真实值');
ylabel('测试集预测值');
xlim([min(T_test) max(T_test)])
ylim([min(T_sim2) max(T_sim2)])
title('测试集预测值 vs. 测试集真实值')

⛄ 运行结果

⛄ 参考文献

[1] 曾鸣,林磊,程文明.基于LIBSVM和时间序列的区域货运量预测研究[J].计算机工程与应用, 2013, 49(21):6-10.DOI:10.3778/j.issn.1002-8331.1303-0342.

[2] 徐恺.基于支持向量机的股指时间序列预测[D].西南交通大学[2023-07-19].DOI:10.7666/d.y1573793.

[3] XIANG Changsheng,ZHOU Ziyingb,向昌盛,等.Pest multiple dimension time series forecasting based on SVM基于支持向量机的害虫多维时间序列预测*[J].计算机应用研究, 2010, 27(10):3694-3697.DOI:10.3969/j.issn.1001-3695.2010.10.023.

⛳️ 代码获取关注我

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料

🍅 仿真咨询

1.卷积神经网络(CNN)、LSTM、支持向量机(SVM)、最小二乘支持向量机(LSSVM)、极限学习机(ELM)、核极限学习机(KELM)、BP、RBF、宽度学习、DBN、RF、RBF、DELM实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3.旅行商问题(TSP)、车辆路径问题(VRP、MVRP、CVRP、VRPTW等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划

4.无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配

5.传感器部署优化、通信协议优化、路由优化、目标定位

6.信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号

7.生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化

8.微电网优化、无功优化、配电网重构、储能配置

9.元胞自动机交通流 人群疏散 病毒扩散 晶体生长