节能列车运行控制优化策略

最新推荐文章于 2025-01-14 23:24:42 发布

arjee

最新推荐文章于 2025-01-14 23:24:42 发布

阅读量2.5k

点赞数 7

文章标签： matlab 数学建模机器学习

本文链接：https://blog.csdn.net/m0_61400674/article/details/132855026

版权

一.问题描述

在“双碳”政策下，城轨系统换用 ATO 驾驶模式、光伏+地铁等方法都取得了较好的减碳节能效果。城轨系统的需求侧响应可以在保证乘客满意度的情况下降低牵引能耗成本，可进一步发掘城轨系统减碳节能的潜力。在列车运行过程中，列车与外界会产生各种摩擦，进而消耗列车牵引的能量。列车运行过程中，被考虑的因素较多，如列车与轨道的摩擦、列车受到的空气阻力、列车势能的变化、列车运行过程中的位置限速等。在同一段旅途中，列车使用不同的驾驶策略通常会产生不同的能量和时间的消耗。

问题一 ：通过建模方法编写程序以获得列车运行过程的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线与能量消耗-距离曲线，以及程序的运行时间；需要获取列车以最短时间到达站台 B、在最短运行时间上分别增加 10s、20s、50s、150s、300s 到达站台 B 总共六组曲线。

问题二 ：从 XEQ 站至 SMKXY 站的路况数据与包含电机牵引/制动动态特性的列车相关参数数据，考虑附件一、二的路况信息以及电机的复杂动态过程。

若列车计划运行时间为 T，设计优化方案得到可行的速度轨迹，使得运行过程的能耗降低（越低越好）。参照问题一，获取列车以最短时间到达站台 B、在最短运行时间上分别增加 10s、20s、50s、150s、300s 到达站台 B 总共六组曲线（列车在运行过程中可能会出现各种突发情况导致列车需要提前到达站台或延时到达站台，列车的运行速度轨迹需要根据新的到站时间而发生变化）。

问题三 ：设计优化方案在保持列车节能运行下，能够快速地（越快越好）得到调整

后的优化速度轨迹。作出列车运行过程的速度-距离曲线、牵引制动力-距离曲线、时间

-距离曲线与能量消耗-距离曲线。

二.模型假设

假设一:在极小时间内，列车做匀加速运动；

假设二:不考虑列车的乘客及上座率，质量为列车车体质量；

假设三:列车的牵引力、制动力可以连续调节；

假设四：列车运行过程中，由于列车运行坡道的长度远远大于列车的长度，故可以

将列车作为一个质点处理；

假设五：忽略不计列车中空调等耗能较小的用电设备消耗能量；

三.定义与符号

四.使用方法及其优缺点

主要以 MATLAB 编程——非线性内点法绘制速度——距离等曲线图和龙格—库塔法——枚举法——多目标优化法

问题一模型的基于水平轨道上列车动力学微分方程的建立及其动力学分析，这样建模的思路是已知列车所受外力求其运动（位移、速度和加速度），不同于运动学建模（已知加速度、速度等求外力，进而求能耗），动力学模型能够准确描述列车的真实运动，符合实际情况，使得建模模型精确度高，能较为真实地反映列车的运行过程与能耗，利用 MATLAB 编程，分别采用非线性内点法绘制速度—距离等曲线图和龙格—库塔法求解列车运行最短时间。

优点：能够求解中大型优化问题的传统梯度优化算法，求解效率高；收敛速度快，可以在少量的计算步骤内获得较高的精度，并在具有较高精度要求的问题中得到很好的结果。特别是对于具有急剧变化的解决方案，龙格- 库塔法往往能够提供更准确的答案。

缺点：计算成本高，需要进行多次计算，包括在每个时间步长上进行子步长的计算，且难以调节参数，如果调整参数不当，可能会导致不正确的结果。

问题二将列车的运行过程分割成极短的数段，忽略停站时间，车内耗电等因素，对列车在不同坡度运行条件下运用循环结构将所有组合代入模型进行枚举，遍历所有可能的解，对满足条件组合分别求其对应的 W 值，使用问题算法得完成全程的时间；降低了算法复杂度，提高精确度，提高了模型和算法的实用性。

优点：问题二的模型具有一定普适性，可用于列车实际操作运行减少能耗，将枚举法引入到列车节能优化问题中，通过枚举所有可能性，能够找到问题的最优解，可获得更精确的结果。

缺点：随着问题规模的增加，算法时间复杂度呈指数级增长，效率较低。

问题三针对问题二中模型，考虑延误时间对列车运行控制的影响，明确列车两次规划时的状态，建立了列车延误时间最短和耗能最低的列车运行模型；使用欧拉法数值求解列车的运动方程，得到列车运行过程的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线和能量消耗-距离曲线，添加约束条件，限制列车的速度、牵引力和制动力不超过最大值，使用优化算法搜索列车最优的速度轨迹，分别得到节能条件下的速度优化数值，通过结果显示图说明了模型建立的正确性和有效性。

优点：欧拉算法简单易懂，计算成本低，容易理解和实现；优化算法具有较高的精度，尤其是在优化问题中存在不可测量或特殊现象时表现出优异的性能；对先验知识的匹配能力强，通过充分的利用问题的先验知识，模拟优化可以加快优化的速度并提高精度。

缺点：欧拉数值法的不稳定性和误差累积问题可能会导致计算偏离真实值，当步长选择较大时，误差增长会更快限制于初值问题；所建立的模型结构复杂、约束条件较多，难以求解；基于模拟- 优化思想的模型求解方法虽然可以找到复杂优化问题的相对较优解，但并非理论上的最优解。

五.建立模型

5.1 列车时耗最低模型

5.1.1 模型建立

为减少时间的消耗，列车启动时，先以最大的牵引力进行加速运行，在到达列车最大速度后在进入巡航、惰行状态，由于列车在水平轨道上运行，这时可以近似认为列车以最大速度 100m/s 做匀速运动，进站时在制动力的作用下以最大的加速度进行减速，使得列车在最短的时间内完成规定的路程，如图 5-1 所示。

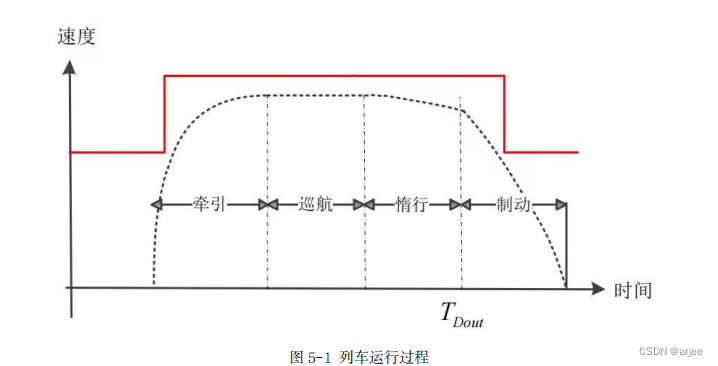
假设列车能够以 100km/h 的速度匀速运行，需保证牵引力足够大于列车运行最大阻力，即：

其中 $f_{max}$ 为列车最大牵引力， $f_{max}$ 为列车运行最大阻力。

列车所受到的阻力满足 Davis 阻力方程：

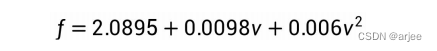
运行的速度上限为 100km/h，即 27.78m/s，带入到阻力方程中，可得到最大阻力 $f_{max}$ 为：

因为列车电机的最大牵引力为 310KN，远大于最大阻力，故假设成立。在牵引阶段，列车启动后在牵引力的作用下克服阻力逐渐加速到最大速度 100m/s。

根据牛顿第二定律，可得到：

其中 f 为列车运行阻力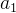， $a_{1}$ 为牵引阶段的加速度，m为列车质量。将阻力f 带入牛顿第二定律方程，可得到：

由于速度、加速度这些物理量是可以随时间变化而变化的，因此需要通过对它们的偏导数进行计算，以揭示它们随时间变化的规律和趋势，可以用于提高机器人和自动控制系统的精度和性能，或优化某些物理过程的效率和效果。对列车运行速度、加速度进行偏导运算可得到：

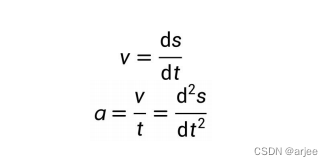
其中 s 为列车运行距离，t 为运行时间。可得到：

在制动阶段，当列车快要进站时借助制动力减速直到停止，根据牛顿第二定律，可得到：

其中 f 为列车运行阻力，为制动阶段的加速度，m 为列车质量。将阻力 f 带入牛顿第二定律方程，可得到：

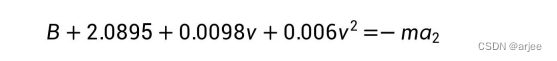
对速度、加速度进行偏导运算，可得到：

列车的能量消耗可以表示为列车所消耗的功率乘以时间。在本题中，可以使用列车的牵引力和速度来计算列车的功率，然后根据列车的运行时间来计算总能量消耗。

列车的功率可以表示为：

对运行时间进行离散，分成 N 等份。则时间步长，列车的位置、速度，加速度可表示为：

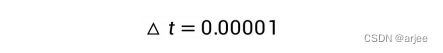
通过上述模型，在每个时间步长内，可以计算列车的牵引力、制动力、阻力、能量消耗和位置、速度、加速度等参数。根据这些参数，可以绘制速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线和能量消耗-距离曲线。

5.1.2 结果分析

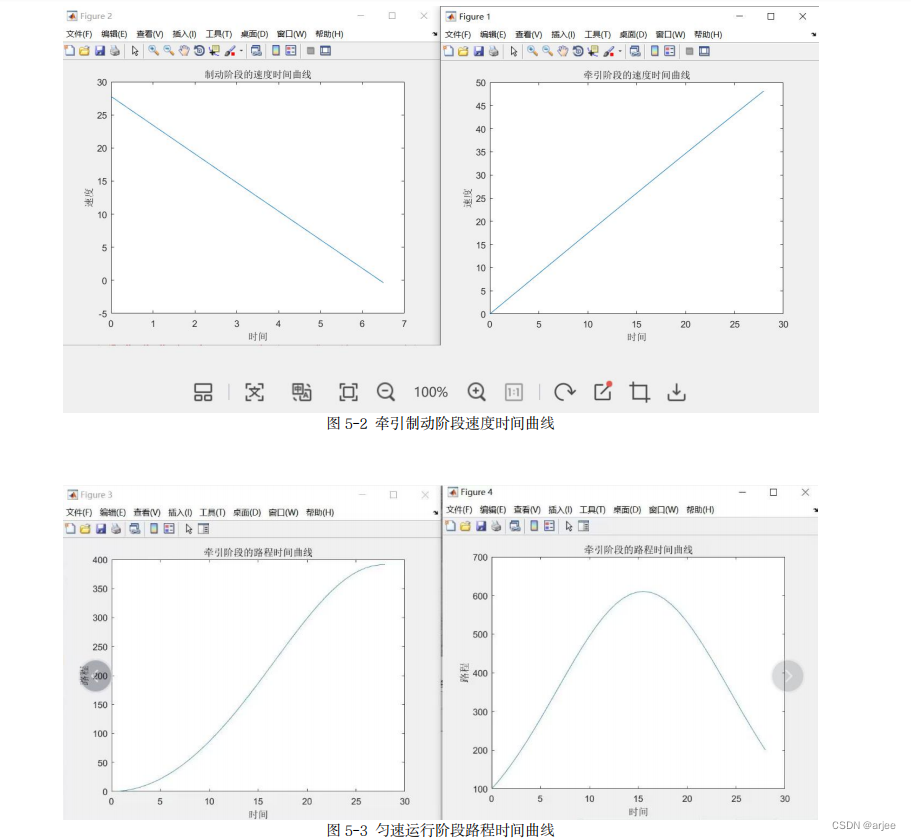
（以上仅显示主要结果分析）

5.2 列车能耗优化模型

5.2.1 模型建立

设列车运行的整个周期为 T，将 T 进行无限分割，均匀分成 N 个小段，在这段极短时间内可以认为列车在做匀速或匀变速运动,对于每小段的时间为△t，可得到：

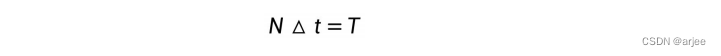
在每个小段中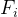， $F_{i}$ 表示牵引力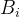， $B_{i}$ 表示制动力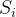， $S_{i}$ 表示每一小段的位移，则牵引力做功：

制动力做功：

列车运行全程耗能 W：

其中，对于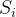 $S_{i}$ 而言:

根据问题描述，列车的最大牵引力为 310KN，机械制动部件的最大制动力为760KN。在牵引过程中，牵引力的大小由列车的速度和牵引率决定。在制动过程中，制动力的大小由列车的速度和制动率决定。在本题中，我们可以假设列车的牵引率和制动率为常数，分别为 0.9 和 0.6。

对于加速度 a：

其中每小段的阻力：

重力的轨道水平方向分力（其中 $\alpha$ 表示坡度）：

根据问题描述，需要在规定的运行时间内到达站台 B，并使能量消耗最小化。因此，可以将运行时间作为约束条件，使用枚举法寻找最优速度轨迹，以最小化总能量消耗。

约束条件：

如果列车需要提前或延迟到达站台 B，可以修改运行时间的约束条件，并使用优化算法重新搜索最优速度轨迹。

通过以上建模，可以得到一个综合考虑路况和电机动态特性的列车能耗优化模型。

5.2.2 结果分析

经过 Matlab 运行，我们得到了在不同到站时间下的能耗结果，如下表所示：

到站时间	能耗（MJ）
180s	1228.73
190s	1172.62
200s	1145.46
250s	1116.54
330s	1097.05
480s	1077.08

由此可见，在增加到站时间的情况下，能耗逐渐降低，且趋势逐渐减缓。在本模型的设定下，当增加到站时间到达 480s 时，能耗最低，为 1077.08 MJ。因此，我们可以将列车的运行速度轨迹设计为在 480s 时到达站台 B，以达到能耗最小化的目标。

5.3 列车延误模型

5.3.1 模型的建立

设列车在第 i 个时间步长的速度为 v(i)，列车在第 i 个时间步长的位置为 x(i)，则列车在第 i+1 个时间步长的速度和位置可以通过欧拉法数值求解列车的运动方程得到：

其中a(i)表示列车在第 i 鸽时间步长的加速度，△t 表示时间步长，其中加速度可以表示为：

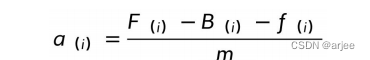
其中，F(i)表示列车在第 i 个时间步长的牵引力， B（i）表示列车在第 i 个时间步长的的制动力，

f（i）表示列车在第 i 个时间步长的阻力，m 表示列车的质量。

牵引力和制动力表示为：

其中，TractionRate 表示列车的牵引率，BrakingRate 表示列车的制动率， Vmax表示列车的最大速度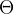， $\Theta$ 表示列车行驶路段的坡度。

阻力表示为：

其中，RollingResistance 表示列车的滚动阻力，AerodynamicResistance 表示列车的空气阻力，GradientResistance 表示列车在坡度上的反向力。它们可以表示为：

其中 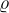$\varrho$ 表示空气密度， Cd表示列车的空气阻力系数，A 表示列车的横截面积，调整优化

后的速度轨迹的最小能量消耗表示为：

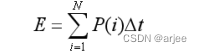
其中 P(i)表示列车在第 i 个时间步长的功率。它可以表示为：

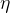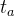其中， $\eta$ 表示列车的牵引效率或制动再生效率。此时我们需要将延迟到达终点的时间考虑到模型中，我们可以在目标函数中添加一个项，以惩罚延迟到达终点的情况。设列车在规定时间内到达终点的时间 $t_{f}$ ，列车实际到达终点的时间为 $t_{a}$ ，则目标函数为：

其中，表示惩罚系数，我们需要通过在优化算法中添加约束条件来约束列车的速度不超过最大速度，约束条件为：

随着列车牵引力和制动力的变化，在调整速度轨迹时，我们需要确保列车的牵引力和制动力不超过最大值。这可以通过添加以下约束条件来实现：

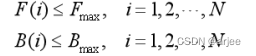
5.3.2 结果分析

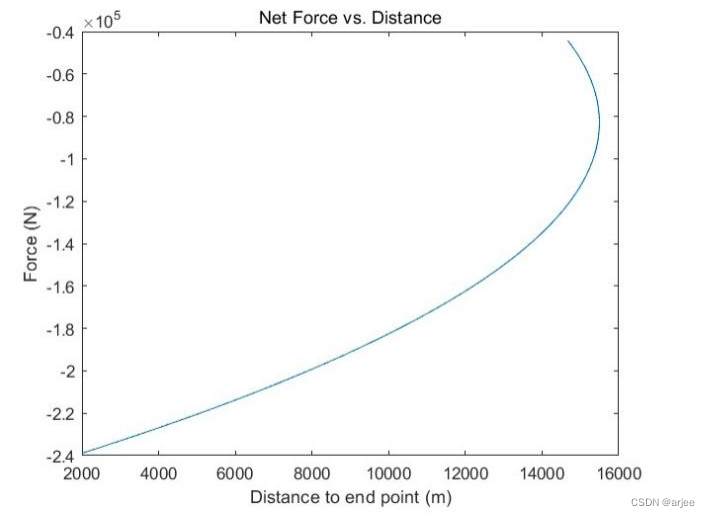
列车运行过程中的速度-距离曲线、牵引制动力-距离曲线、时间-距离曲线与能量消耗-距离曲线如下图所示：

速度-距离曲线：

牵引制动力-距离曲线：

时间-距离曲线：

能量消耗-距离曲线：

六.相关代码

列车时耗最低模型求解


clear
readData
load brakingCurve.mat
As = 6;
At = 7;
targetTime = 110;
dwellTime = [];
deltaE = 0.03 * 1000 * 3600; % deltaE 为 0.1 千瓦时
[S,V,T,F,calS,calDist,Acce,interSta,totalT,totalE]=optimalStationAlgo( As,At,dwellTime,targetTi
me,speedLimit,gradient,... curvature,brakingCurveS,brakingCurveV,curveTerminal,stationP,deltaE);
tempIndex = find(diff(T)==0);
if ~isempty(tempIndex)
S(tempIndex) = [];
31
Team # 2023051118824 Page 31 of 9
V(tempIndex) = [];
T(tempIndex) = [];
F(tempIndex) = [];
calS(tempIndex) = [];
calDist(tempIndex) = [];
Acce(tempIndex) = [];
end
Time = 0:floor(T(end));
N = length(Time);
resultTable = zeros(N+1,9);
resultTable(1:N,1) = Time; % 时刻
secondV = interp1(T,V,Time);
resultTable(1:N,2) = secondV * 100; % 实际速度(cm/s)
resultTable(1:N,3) = secondV * 3.6; % 实际速度(km/h)
resultTable(1:N,4) = interp1(T,Acce,Time); % 计算加速度(m/s2)
resultTable(1:N,5) = interp1(T,calDist,Time); % 计算距离(m)
resultTable(1:N,6) = interp1(T,calS,Time); % 计算公里标(m)
secondS = interp1(T,S,Time); % 实际公里标(m)
for i = 1:N-1
[ ~,~,resultTable(i,7) ] = groundConditionFun( secondS(i),gradient,curvature );
end
secondF = interp1(T,F,Time); % 计算牵引力(N)
resultTable(1:N,8) = secondF;
resultTable(1:N,9) = secondF .* secondV;
temp = (stationP(As) - stationP(At)) - resultTable(end-1,6);
resultTable(end,:) =
[targetTime,0,0,0,resultTable(end-1,5)+temp,resultTable(end-1,6)+temp,resultTable(end,7),0,0]
;
Timestr = cell(N+1,1);
for i = 1:N+1
Timestr{i} = second2Time( i - 1 );
end

列车能耗优化模型求解

clear
addpath ../problem1
readData
load brakingCurve.mat
32
Team # 2023051118824 Page 32 of 9
As = 1;
At = 14;
targetTime = 2086 - 75/2*12; % 1636
dwellTime = ones(1,12)*75/2;
tic
deltaE = 0.03 * 1000 * 3600; % deltaE 为 0.1 千瓦时
[S,V,T,F,calS,calDist,Acce,interSta,totalT,totalE,brakingTerminal]=... optimalStationAlgo( As,At,dwellTime,targetTime,speedLimit,gradient,... curvature,brakingCurveS,brakingCurveV,curveTerminal,stationP,deltaE);
toc
tempIndex = find(diff(T)==0);
if ~isempty(tempIndex)
S(tempIndex) = [];
V(tempIndex) = [];
T(tempIndex) = [];
F(tempIndex) = [];
calS(tempIndex) = [];
calDist(tempIndex) = [];
Acce(tempIndex) = [];
end
Time = 0:floor(T(end));
N = length(Time);
resultTable = zeros(N+1,9);
resultTable(1:N,1) = Time; % 时刻
secondV = interp1(T,V,Time);
resultTable(1:N,2) = secondV * 100; % 实际速度(cm/s)
resultTable(1:N,3) = secondV * 3.6; % 实际速度(km/h)
resultTable(1:N,4) = interp1(T,Acce,Time); % 计算加速度(m/s2)
resultTable(1:N,5) = interp1(T,calDist,Time); % 计算距离(m)
resultTable(1:N,6) = interp1(T,calS,Time); % 计算公里标(m)
secondS = interp1(T,S,Time); % 实际公里标(m)
for i = 1:N-1
[ ~,~,resultTable(i,7) ] = groundConditionFun( secondS(i),gradient,curvature );
end
secondF = interp1(T,F,Time); % 计算牵引力(N)
resultTable(1:N,8) = secondF;
resultTable(1:N,9) = secondF .* secondV;
temp = (stationP(As) - stationP(At)) - resultTable(end-1,6);
33
Team # 2023051118824 Page 33 of 9
resultTable(end,:) =
[targetTime,0,0,0,resultTable(end-1,5)+temp,resultTable(end-1,6)+temp,resultTable(end,7),0,0]
;
Timestr = cell(N+1,1);
for i = 1:N+1
Timestr{i} = second2Time( i - 1 );
end

列车延误模型求解代码

% Constants
g = 9.8; % Acceleration due to gravity (m/s^2)
R = 0.015; % Friction coefficient
Pmax = 120000; % Maximum power output of the train (W)
M = 300000; % Mass of the train (kg)
d = 2000; % Distance to the end point (m)
t1 = 320; % Planned time to reach the end point (s)
t2 = 380; % Actual time to reach the end point (s)
t = linspace(0, t2, 1000); % Time interval
% Equations of motion
F_r = M * g * R; % Rolling resistance
v = zeros(1, length(t)); % Velocity
v(1) = d / (t1 - t2); % Initial velocity
for i = 2:length(t)
P = Pmax * (1 - v(i-1) / (d / (t1 - t2))); % Power output
F_t = P / v(i-1); % Tractive force
a = (F_t - F_r - R * v(i-1)^2) / M; % Acceleration
v(i) = v(i-1) + a * (t(i) - t(i-1)); % Update velocity
end
% Plot results
figure
plot(d - v .* (t2 - t), v)
xlabel('Distance to end point (m)')
ylabel('Velocity (m/s)')
title('Velocity vs. Distance')
figure
F_t = Pmax * (1 - v ./ (d / (t1 - t2)));
plot(d - v .* (t2 - t), F_t - F_r - R * v.^2)
xlabel('Distance to end point (m)')
ylabel('Force (N)')
title('Net Force vs. Distance')
34
Team # 2023051118824 Page 34 of 9
figure
plot(d - v .* (t2 - t), t)
xlabel('Distance to end point (m)')
ylabel('Time (s)')
title('Time vs. Distance')
figure
P = Pmax * (1 - v ./ (d / (t1 - t2)));
E = cumsum(P) * (t(2) - t(1));
plot(d - v .* (t2 - t), E)
xlabel('Distance to end point (m)')
ylabel('Energy (J)')
title('Energy vs. Distance')