PyTorch第九讲 Softmax分类器

Softmax分类器

在多分类问题中，我们希望最终的输出是一个分布，满足$P(y=i)\ge 0$且${\sum }_{i=0}^{n}P(y=i)=1$，因此我们采用Softmax而不是之前的Sigmoid
P ( y = i ) = e Z i ∑ j = 0 K − 1 e Z j , i ∈ { 0 , … , K − 1 } P(y=i)=\frac{e^{Z_i}}{\sum_{j=0}^{K-1}e^{Z_j}},i\in\{0,\ldots,K-1\} P(y=i)=∑j=0K−1​eZj​eZi​​,i∈{0,…,K−1}

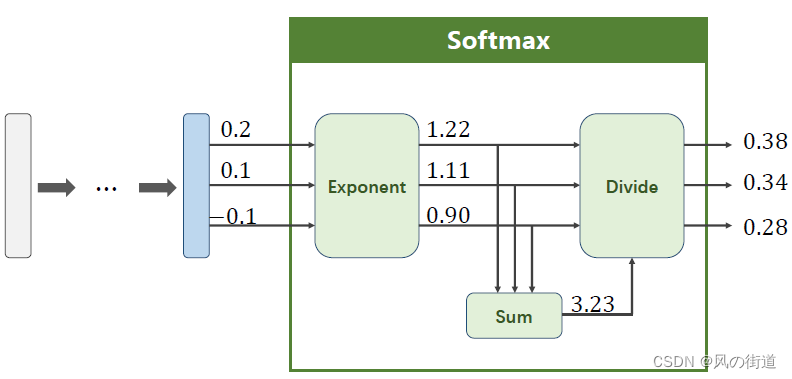
NLLLoss损失函数

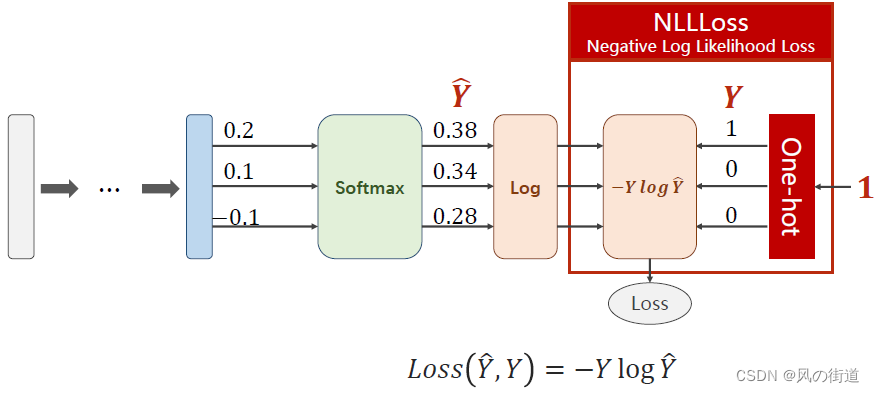
$$Loss(\hat{Y},Y)=-Y\log \hat{Y}$$
需要现在NLLLoss之前把softmax输出的数值求lg值

代码实现

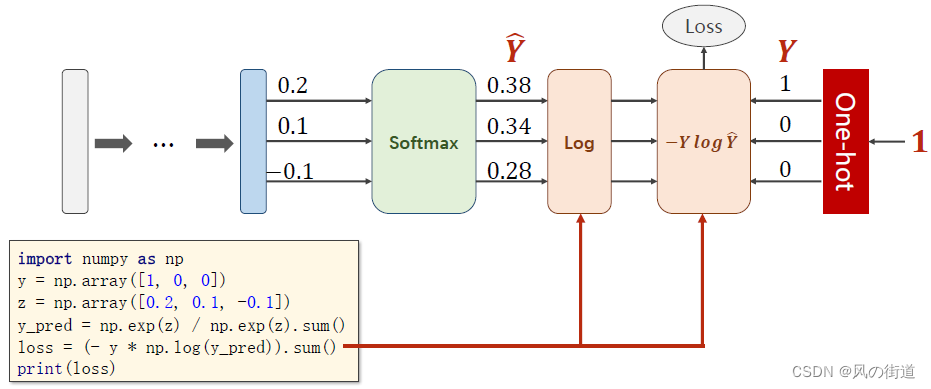
不用pytorch实现

用pytorch实现

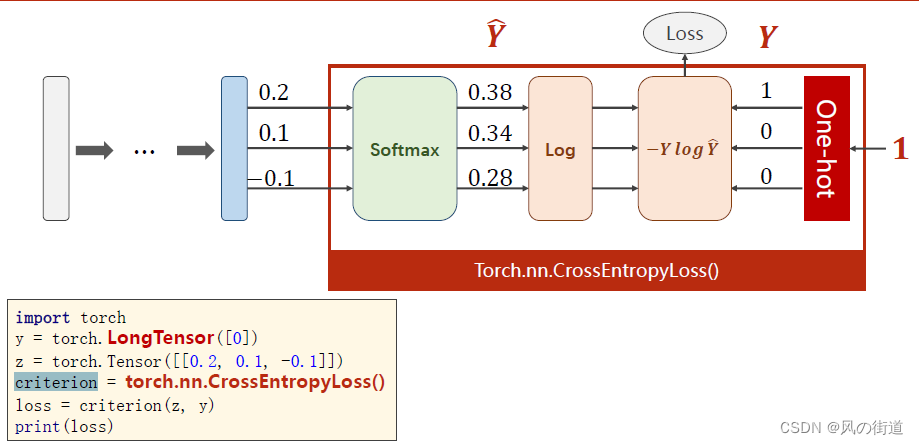
注意，y要用torch中的LongTensor类型,这里面[0]对应图中One-hot的1 0 0 即指出第一个数为1

具体代码

这里面Y的2，0，1的意思分别是3次真实结果中分别是第3，1，2个数为1，其余为0

实例代码

import torch
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision import transforms      #将w（宽）×h（高）×c（channel）转换成c×w×h，即把通道提到最前面

batch_size = 64
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))      #mnist数据集的均值，前人已经算好的，直接用这两个数就行
])

train_dataset = datasets.MNIST(root='./dataset/minist/',
                               train=True,
                               download=True,
                               transform=transform)
train_loader = DataLoader(train_dataset,
                          shuffle=True,
                          batch_size=batch_size)
test_dataset = datasets.MNIST(root='./dataset/mnist/',
                              train=False,
                              download=True,
                              transform=transform)
test_loader = DataLoader(test_dataset,
                         shuffle=False,
                         batch_size=batch_size)


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)

    def forward(self, x):
        x = x.view(-1, 784) #-1的意思是让电脑自动计算把这些数分成784列时有多少行
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x)       #最后一层不需要激活，因为后面用到的损失函数的输入需要的是未激活的值


model = Net()

criterion = torch.nn.CrossEntropyLoss() #交叉熵
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)        #momentum：动量，有助于更快收敛，也有助于跳出局部最优


def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad()

        #前馈+反馈+更新
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0
    total = 0
    with torch.no_grad():       #test不需要算梯度
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)   # 用_表示一个不重要的值，后面也没用到，就只占个位置，dim=1表示横向求max
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print('Accuracy on test set: %d %%' % (100 * correct/total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

[1,   300] loss: 2.155
[1,   600] loss: 0.788
[1,   900] loss: 0.411
Accuracy on test set: 89 %
[2,   300] loss: 0.310
[2,   600] loss: 0.270
[2,   900] loss: 0.227
Accuracy on test set: 93 %
[3,   300] loss: 0.178
[3,   600] loss: 0.183
[3,   900] loss: 0.150
Accuracy on test set: 95 %
[4,   300] loss: 0.136
[4,   600] loss: 0.120
[4,   900] loss: 0.114
Accuracy on test set: 96 %
[5,   300] loss: 0.102
[5,   600] loss: 0.095
[5,   900] loss: 0.086
Accuracy on test set: 96 %
[6,   300] loss: 0.082
[6,   600] loss: 0.071
[6,   900] loss: 0.072
Accuracy on test set: 97 %
[7,   300] loss: 0.062
[7,   600] loss: 0.060
[7,   900] loss: 0.060
Accuracy on test set: 97 %
[8,   300] loss: 0.051
[8,   600] loss: 0.046
[8,   900] loss: 0.050
Accuracy on test set: 97 %
[9,   300] loss: 0.039
[9,   600] loss: 0.039
[9,   900] loss: 0.044
Accuracy on test set: 97 %
[10,   300] loss: 0.028
[10,   600] loss: 0.032
[10,   900] loss: 0.036
Accuracy on test set: 97 %

课后作业

Try to implement a classifier for:

• Otto Group Product Classification Challenge
• Dataset: Kaggle数据集