题目描述
Drawing flags is a boring job. But it is nice to do this.
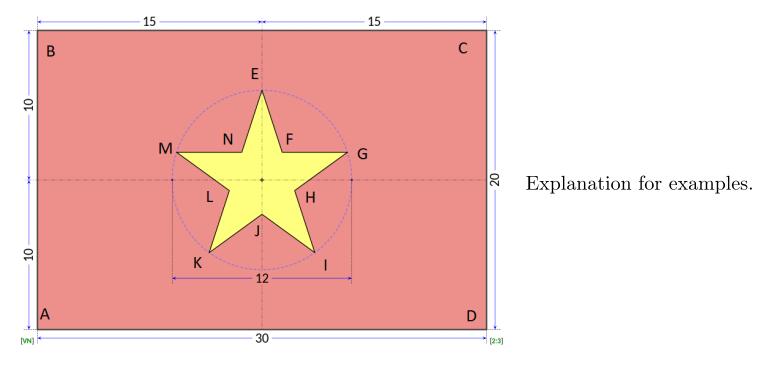
Given the coordinates of the point A and point B in the flag. You should output the coordinates of C, D,E, F, G, H, I, J, K, L, M and N.
The flag:
It is possible to scale the flag down or scale the flag up when drawing. So it is possible that |AB| ≠ 20.输入
The first line contains a single integer t (1 ≤ t ≤ 5000), the number of test cases. Then t test cases follow.
Each line contains 4 integers xA, yA, xB and yB separated by a space — the coordinates of the point A(xA, yA) and point B(xB, yB) (−105 ≤ x, y ≤ 105).输出
For each test case output 1 line.
Each line contains 24 real numbers
xC, yC, xD, yD, xE, yE, xF , yF , xG, yG, xH, yH, xI , yI , xJ , yJ , xK, yK, xL, yL, xM , yM , xN and yN separated by space — the coordinates of the point C(xC, yC), point D(xD, yD), point E(xE, yE), point F(xF , yF ),point G(xG, yG), point H(xH, yH), point I(xI , yI ), point J(xJ , yJ ), point K(xK, yK), point L(xL, yL),point M(xM , yM ) and point N(xN , yN ).样例输入 Copy
1 0 0 0 20样例输出 Copy
30.000000 20.000000 30.000000 -0.000000 15.000000 16.000000 16.347084 11.854102 20.706339 11.854102 17.179628 9.291796 18.526712 5.145898 15.000000 7.708204 11.473288 5.145898 12.820372 9.291796 9.293661 11.854102 13.652916 11.854102.提示
Your answer will be considered correct if its absolute or relative error does not exceed 10−6. Formally let your answer be a and jury’s answer be b. Your answer will be considered correct if


#include<bits/stdc++.h>
#define db double
using namespace std;
const int N=2e5+7;
const int mod=1e9+7;
const double pi=acos(-1.0);
const double eps=1e-8;
struct P{
db x,y;P(db X=0,db Y=0){x=X,y=Y;}
inline void in(){scanf("%lf%lf",&x,&y);}
inline void out(){printf("%.6lf %.6lf ",x,y);}
}a,b,c,d,e,f,g,h,i,j,k,l,m,n,o;
inline db Dot(P a,P b){return a.x*b.x+a.y*b.y;}
inline db Cro(P a,P b){return a.x*b.y-a.y*b.x;}
inline db Len(P a){
return sqrt(Dot(a,a));
}
inline P turn_PP(P a,P b,db theta){
db x=(a.x-b.x)*cos(theta)+(a.y-b.y)*sin(theta)+b.x;
db y=-(a.x-b.x)*sin(theta)+(a.y-b.y)*cos(theta)+b.y;
return P(x,y);
}
double ps,r;
void Solve(){
a.in();b.in();
P v1(b.x-a.x,b.y-a.y);
P v2(3*v1.y/2,-3*v1.x/2);
d.x=a.x+v2.x,d.y=a.y+v2.y;
c.x=b.x+v2.x,c.y=b.y+v2.y;
o.x=(a.x+c.x)/2.0,o.y=(a.y+c.y)/2.0,ps=sin(pi*18/180.0)/sin(pi*126/180.0);
e.x=o.x+v1.x*3/10,e.y=o.y+v1.y*3/10;
j.x=o.x-v1.x*3/10*ps,j.y=o.y-v1.y*3/10*ps;
g=turn_PP(e,o,pi*2/5);
i=turn_PP(e,o,pi*4/5);
k=turn_PP(e,o,pi*6/5);
m=turn_PP(e,o,pi*8/5);
l=turn_PP(j,o,pi*2/5);
n=turn_PP(j,o,pi*4/5);
f=turn_PP(j,o,pi*6/5);
h=turn_PP(j,o,pi*8/5);
c.out();
d.out();
e.out();
f.out();
g.out();
h.out();
i.out();
j.out();
k.out();
l.out();
m.out();
n.out();
}
int main(){
int T=1;
cin>>T;
while(T--){
Solve();
}
return 0;
}







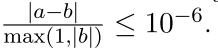
















 657
657

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








