概念
支持向量机(Support Vector Machine,SVM)是一种在机器学习中广泛应用的监督学习算法,主要用于数据的二分类问题。它的基本理念是寻找一个最优的超平面,这个超平面可以在特征空间中最大化两个类别之间的间隔,从而最完美地将两类数据分开。SVM的目标是最小化超平面的错误分类,同时最大化分类边界的间隔,以提高其泛化能力。
优点和缺点
优点:
1. 泛化能力:SVM通过最大化分类间隔来提高模型的泛化能力,这意味着它在处理未见过的数据时通常能表现得很好。
2. 小样本学习:SVM能够在只有少量训练样本的情况下仍然学习到有效的分类模型,这使得它非常适合处理小样本问题。
3. 处理高维数据:SVM通过核函数可以将数据映射到高维空间,从而有效地处理高维数据集。
4. 鲁棒性:SVM在处理异常值和噪声时具有较强的鲁棒性,因为它只关注支持向量,而支持向量通常代表了数据的主要结构。
5. 灵活性和多样性:通过选择不同的核函数,SVM可以适用于多种不同的数据分布和问题。
6. 无需依赖整个数据集:SVM的最终决策函数只由支持向量决定,这意味着它不需要依赖整个数据集来做出预测。
缺点:
1. 计算复杂度高:对于大规模的数据集,SVM需要大量的计算资源和时间来找到最优的超平面。
2. 对缺失数据敏感:SVM对缺失数据比较敏感,因为缺失数据可能会导致错误的支持向量。
3. 核函数选择困难:对于非线性问题,选择合适的核函数是一个挑战,错误的核函数可能导致模型性能不佳。
4. 解释性差:SVM在高维空间中工作,这使得模型的解释性较差,难以理解模型的决策过程。
5. 只支持二分类:标准的SVM只能处理二分类问题,对于多分类问题需要采用额外的策略,如一对多(One-vs-All)或二叉树结构。
6. 对参数敏感:SVM模型的性能对某些参数(如惩罚参数C、核函数参数)非常敏感,需要仔细调整以获得最佳性能。
原理
我们可知svm算法其实现过程中即是需要我们将数据集中的一些数据点进行二分,而将这些数据分开的平面就称为分割超平面,而当数据是二维的时候这些分割超平面是一条直线,而当数据是三维的时候分割超平面则为一个平面。而这个分割超平面可以有无数个,但是分割效果最好的也就是几何间隔最大那个分割超平面却只能有一个。也就是说我们若想找出最佳的决策边界也就是找出几何间隔最大的分离超平面。
我们首先可以得超平面的公式如下:
![]()
则我们可以得到数据集中的任意一个点到超平面的距离为
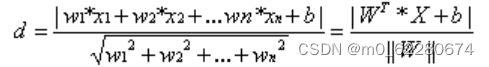
现在我们已经知道了如何去求数据点到超平面的距离,在超平面确定的情况下,我们就能够找出所有支持向量,然后计算出间隔margin。每一个超平面都对应着一个margin,我们的目标就是找出所有margin中最大的那个值对应的超平面。因此用数学语言描述就是确定w、b使得margin最大。这是一个优化问题其目标函数可以写成 :
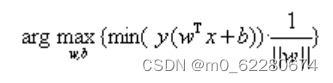
其中y表示数据点的标签,且其为-1或1。距离用计算,这是就能体会出-1和1的好处了。如果数据点在平面的正方向(即+1类)那么是一个正数,而当数据点在平面的负方向时(即-1类),依然是一个正数,这样就能够保证始终大于零了。注意到当w和b等比例放大时,d的结果是不会改变的。因此我们可以令所有支持向量的u为1,而其他点的u大1这是可以办通过调节w和b求到的。因此上面的问题可以简化为:
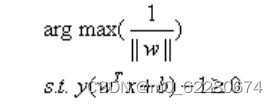
为了后面计算的方便,我们将目标函数等价替换为:
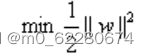
这是一个有约束条件的优化问题,通常我们可以用拉格朗日乘子法来求解,应用拉格朗日乘子法如下:
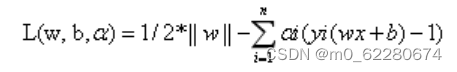 公式1
公式1
求L关于求偏导数得:
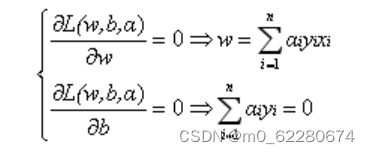 公式2
公式2
将公式2代入到公式1中化简得:
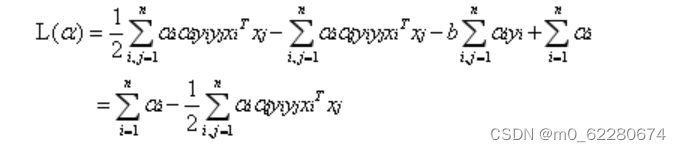
该对偶问题的KKT条件为:

svm算法实现鸢尾花分类
svm算法:
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
for i in range(len(data)):
if data[i,-1] == 0:
data[i,-1] = -1
return data[:,:2], data[:,-1]
#使用RBF(Radial basis function)核函数处理
def K(x,z,sigma=1.5):
return np.exp(np.dot((x-z),(x-z).T)/-(2*sigma**2))
#对应课本147页的g(x_i),该函数助于验证KKT条件
def g(i,x,y,alpha,b):
sum=b
for j in range(len(y)):
sum+=alpha[j]*y[j]*K(x[i],x[j])
return sum
#验证第i个样本点是否满足KKT条件
def isKKT(alpha,i,x,y,b,C):
if alpha[i]==0 and y[i]*g(i,x,y,alpha,b)>=1:
return True
elif alpha[i]==C and y[i]*g(i,x,y,alpha,b)<=1:
return True
elif alpha[i]>0 and alpha[i]<C and y[i]*g(i,x,y,alpha,b)==1:
return True
else:
return False
#验证第i个样本点违反KKT条件的程度。由于KKT条件和y_i*g(x_i)与1的不等式有关
#因此计算y_i*g(x_i)与1之间差值的绝对值作为衡量违反程度的标准
def vioKKT(alpha,i,x,y,b):
return abs(y[i]*g(i,x,y,alpha,b)-1)
#在数组x中找到值为a的元素第一次出现的位置
def findindex(x,a):
for i in range(len(x)):
if x[i]==a:
return i
#某个样本点分类误差函数
def E(w,b,x_k,y_k):
predi_k=int(np.sign(np.dot(w,x_k.T)+b))
return predi_k-y_k
#计算样本点与分割直线的距离
def distance_count(x,w,b):
return abs(w[0]*x[0]+w[1]*x[1]+b) / np.sqrt(w[0]**2 + w[1]**2)测试函数:
from functions import *
from numpy import *
from random import *
from matplotlib import pyplot as plt
def train(C=1.0):
#获得数据集
x,y=create_data()
#设定迭代次数为100次
iter=100
#样本容量也就是标签的个数
N=len(y)
#alpha的初始值取全0
alpha=zeros(len(y))
#设置i,j的初始值(对应alpha1和alpha2)
i,j=randint(0,N-1),randint(0,N-1)
#保证i≠j
while i==j:
i=randint(0,N-1)
for k in range(iter):
#x的尺寸为一个1×2行向量
x_i,x_j=x[i],x[j]
#y的取值为+1或-1
y_i,y_j=y[i],y[j]
#计算ita,为计算a2_newunc做准备
ita=K(x_i,x_i)+K(x_j,x_j)-2*K(x_i,x_j)
if ita==0:
continue
#计算分割平面参数w与b
#x:100×2矩阵,w:1×2矩阵
#由于y-dot(w,x.T)是个与y等长的行向量,取其各元素平均值
w=dot(alpha*y,x)
b=mean(y-dot(w,x.T))
#计算误差E1和E2
E_i=E(w,b,x_i,y_i)
E_j=E(w,b,x_j,y_j)
#计算a2_ewunc
a1_old=alpha[i]
a2_old=alpha[j]
a2_newunc=a2_old+y_j*(E_i-E_j)/ita
#计算L与H
L,H=0.0,0.0
if y_i!=y_j:
L=max(0,a2_old-a1_old)
H=min(C,C+a2_old-a1_old)
elif y_i==y_j:
L=max(0,a2_old+a1_old-C)
H=min(C,a2_old+a1_old)
#计算剪辑后a2_new与a1_new的值
a2_new=max(L,min(H,a2_newunc))
a1_new=a1_old+y_i*y_j*(a2_old-a2_new)
#更新alpha
alpha[i],alpha[j]=a1_new,a2_new
#violation表示每个元素违反KKT条件的程度
violation=zeros(N)
#对每一个样本点检验KKT条件,在violation内记录每个样本点违反KKT的程度
for k in range(N):
if isKKT(alpha,k,x,y,b,C)==False:
violation[k]=float(vioKKT(alpha,k,x,y,b))
#如果没有违反KKT条件,则违反程度是0
else:
violation[k]=0.0
#找到violation中违反程度最大的点,设定为i,对应alpha_1
i=findindex(violation,max(violation))
#这里设置j(对应alpha_2)为不等于i的随机数。
#原本alpha_2的选取应该是令abs(E_i-E_k)最大的k值对应的alpha点
#经过测试,在大多数情况下,abs(E_i-E_k)(1×100向量)的所有元素都是0
#即预测每个元素都准确,每个元素的分类误差都是0,误差的差值也是0
#只有少数情况下,会有一个误差差值不等于0
#对于前一种情况,无所谓“最大的误差差值”(因为都是0),因此只能设置j为随机数
#对于后一种情况,由于出现的次数少,并且那一个不为0的差值的元素出现的位置具有随机性
#因此总是将j设定为随机数
j=randint(0,N-1)
while j==i:
j = randint(0, N - 1)
#计算最终(迭代100次)分割平面参数
w = dot(alpha * y, x)
b = mean(y - dot(w, x.T))
draw_x, draw_y, draw_label = [], [], []
#在散点图上标记样本点的位置,样本点第一个元素作为x坐标,第二个元素作为y坐标
for p in x:
draw_x.append(p[0])
draw_y.append(p[1])
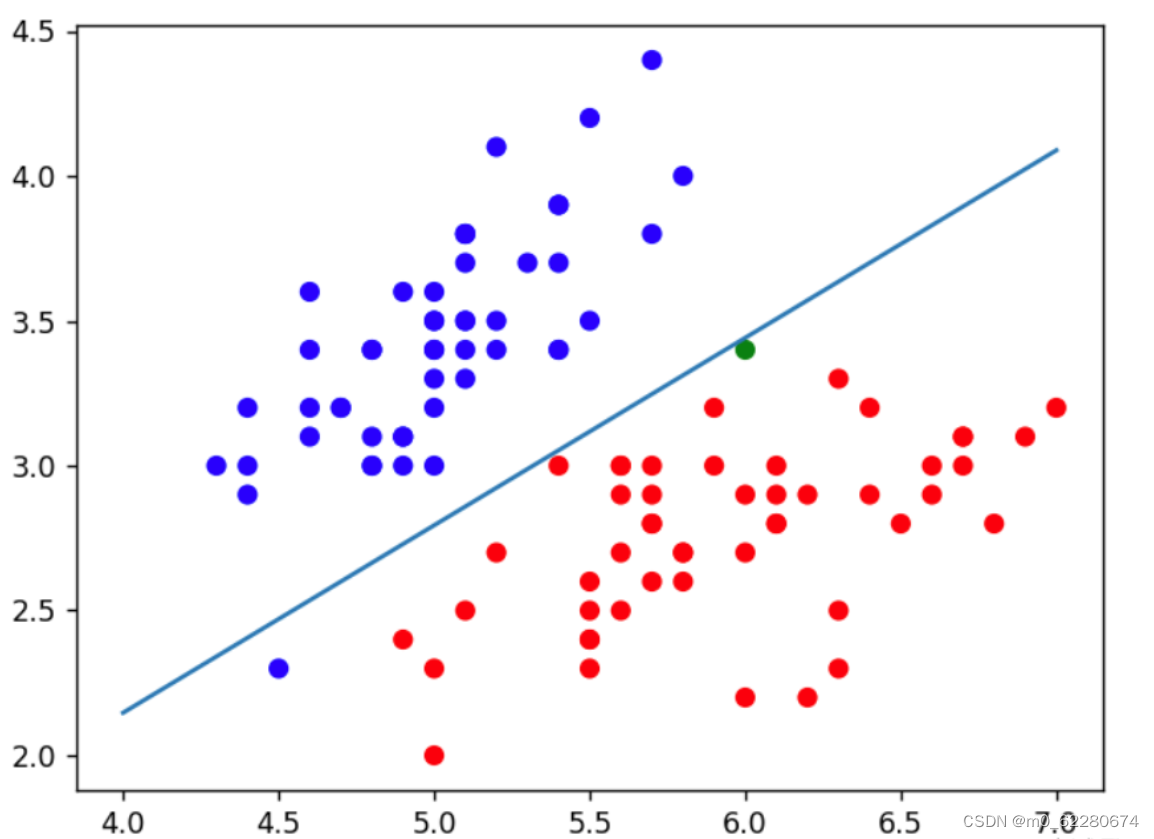
#画散点图,其中支持向量呈现绿色,正类呈现红色,负类呈现蓝色
#样本点离分割直线最近的为支持向量
distance=zeros(len(y))
for i in range(len(y)):
distance[i]=distance_count(x[i],w,b)
vector=findindex(distance,min(distance))
for i in range(len(y)):
if i==vector:
draw_label.append('g')
else:
if y[i] > 0:
draw_label.append('r')
else:
draw_label.append('b')
plt.scatter(draw_x, draw_y, color=draw_label)
plain_x = range(4, 8, 1)
plain_y = []
for i in plain_x:
temp = double(-(w[0] * i + b) / w[1])
plain_y.append(temp)
plt.plot(plain_x, plain_y)
#最终绘图
plt.savefig('SMO.jpg')
plt.show()
if __name__ == '__main__':
train()结果:





















 1512
1512











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








