基于python实现pca（主成分分析）原理和实现

一、PCA的概念

1.1实现背景

在许多领域的数据的分析和处理中，往往会有许多复杂的变量，变量与变量之间通常还存在着相关性，要从大量的变量中提取出能反映事物特征的信息是极其困难的，对单个的变量分析不全面，并且会损失信息，造成错误的结论。主成分分析（PCA）便是通过数学降维，找出最能决定数据特性的主元成分的数据分析方法，用较少的综合指标，揭示隐藏在多维复杂数据变量背后的简单结构，得到更为科学有效的数据信息。

PCA 的实现背景可以追溯到19世纪的协方差矩阵理论。然而，PCA 的现代形式最早由卡尔·皮尔逊（Karl Pearson）在1901年提出，并在20世纪上半叶得到了进一步的发展。

PCA 的核心思想是通过线性变换将原始数据投影到新的坐标系中，使得投影后的数据具有最大的方差。这意味着在新坐标系中的第一个主成分（Principal Component，PC）所包含的信息量最大。然后，通过寻找与第一个主成分正交的方向上的第二个主成分，以及后续的主成分，可以逐步捕捉数据中的剩余方差。

1.2PCA的降维介绍

PCA（Principal Component Analysis）是一种常用的数据降维技术，通过线性变换将原始数据映射到新的低维空间中，保留原始数据中的大部分信息。PCA 的基本思想是，寻找一个正交基使得在这个基上的方差最大，从而达到降维的目的。

在平时的数学建模中，需要用到降维操作：

比如在图像处理中，如果要识别人脸，需要将每张图像表示为一个向量，每个元素代表图像中某个像素点的灰度值。由于每张图像的像素数量很大，可能成百上千万甚至更多，这会导致计算和存储成本非常高。

在这种情况下，可以使用PCA对这些向量进行降维，将每张图像表示为一个包含较少元素的向量，从而使得计算和存储成本大大降低。同时，PCA还能够从这些低维向量中提取出最具代表性的信息，以便于后续s的人脸识别任务。

如下图所示：

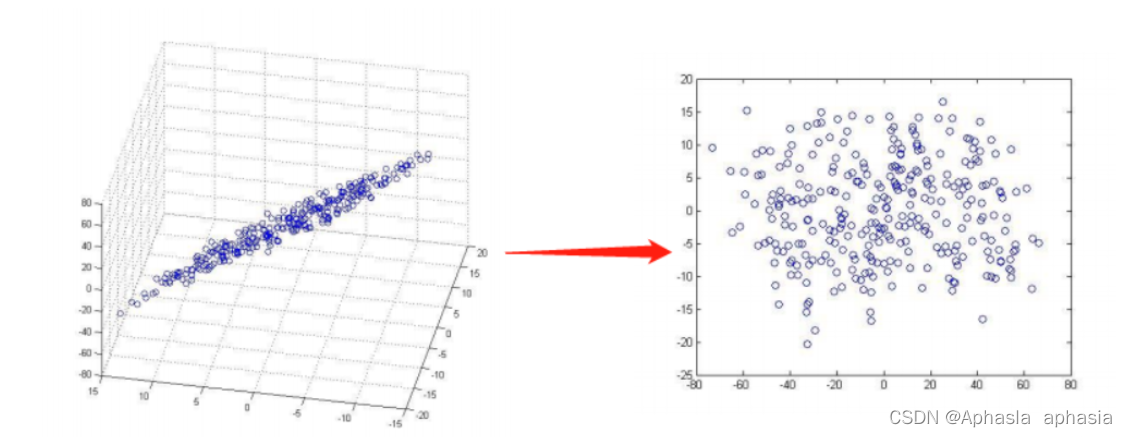
二、PCA要到的数学原理介绍

2.1向量的内积

这是两个向量的 A 和 B 内积：

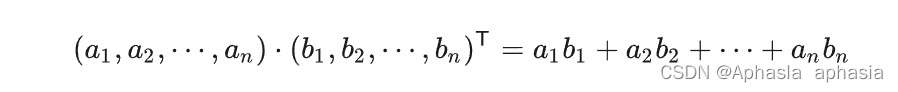
内积运算将两个向量映射为实数，其计算方式非常容易理解，但我们无法看出其物理含义。接下来我们从几何角度来分析，为了简单起见，我们假设 A 和 B 均为二维向量，则：

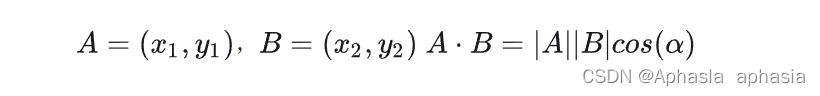
它的几何意义为：

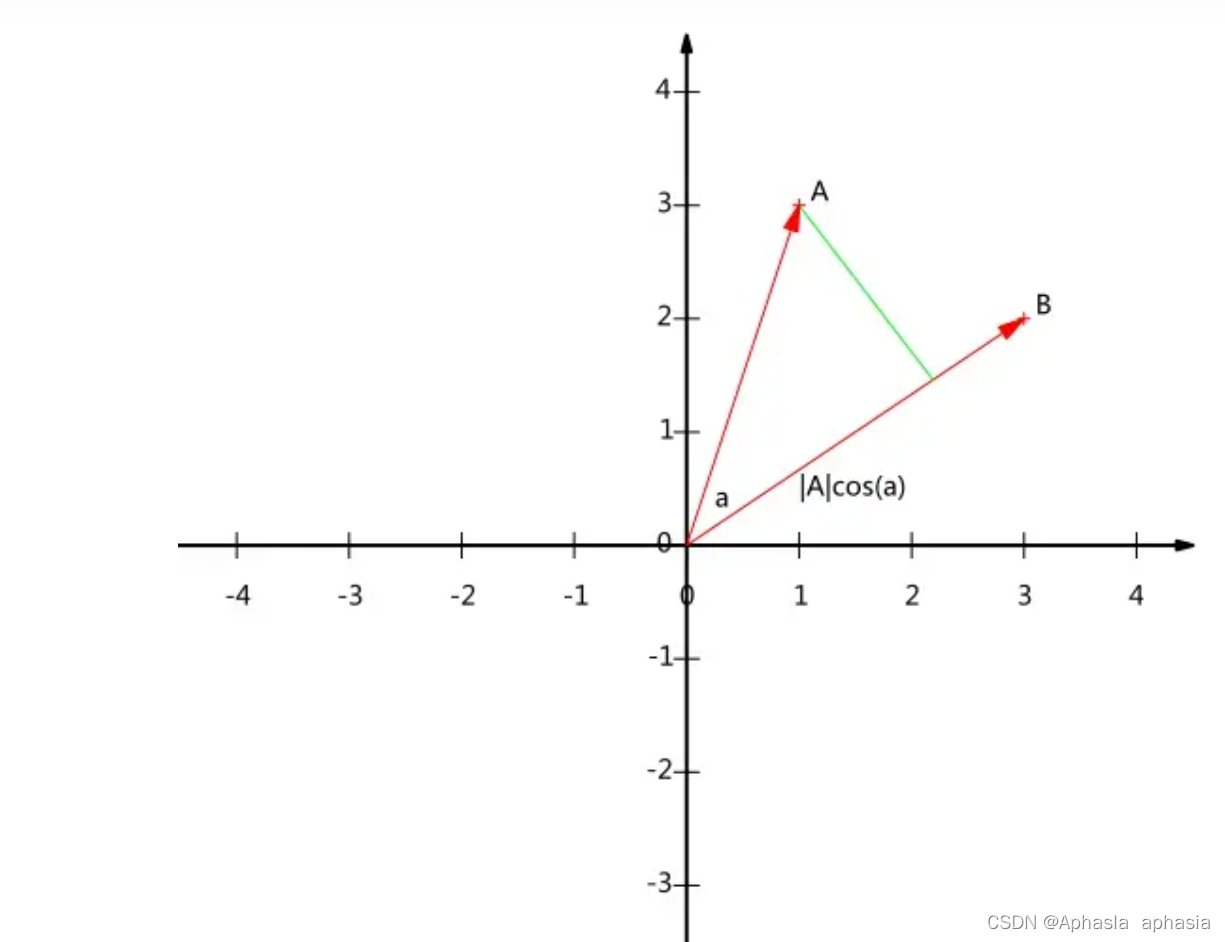
我们看出 A 与 B 的内积等于 A 到 B 的投影长度乘以 B 的模。如果假设 B 的模为 1，就变为了：

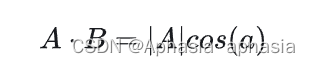
2.2基

在我们常说的坐标系种，向量 (3,2) 其实隐式引入了一个定义：以 x 轴和 y 轴上正方向长度为 1 的向量为标准。向量 (3,2) 实际是说在 x 轴投影为 3 而 y 轴的投影为 2。注意投影是一个标量，所以可以为负。

所以，对于向量 (3, 2) 来说，如果我们想求它在 (1,0),(0,1) 这组基下的坐标的话，分别内积即可。当然，内积完了还是 (3, 2)。

所以，我们大致可以得到一个结论，我们要准确描述向量，首先要确定一组基，然后给出在基所在的各个直线上的投影值，就可以了。为了方便求坐标，我们希望这组基向量模长为 1。因为向量的内积运算，当模长为 1 时，内积可以直接表示投影。然后还需要这组基是线性无关的，我们一般用正交基，非正交的基也是可以的，不过正交基有较好的性质。

2.3基变换的矩阵表示

对于向量 (3,2) 这个点来说，在（ ，）和 （ ，） 这组基下的坐标是多少？

我们拿 (3,2) 分别与之内积，得到（，）这个坐标。

我们可以用矩阵相乘的形式简洁的表示这个变换：

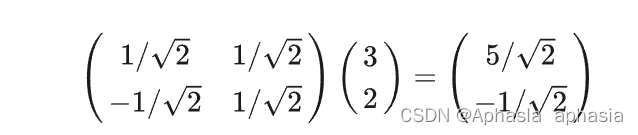
左边矩阵的两行分别为两个基，乘以原向量，其结果刚好为新基的坐标。推广一下，如果我们有 m 个二维向量，只要将二维向量按列排成一个两行 m 列矩阵，然后用“基矩阵”乘以这个矩阵就可以得到了所有这些向量在新基下的值。例如对于数据点 (1,1)，(2,2)，(3,3) 来说，想变换到刚才那组基上，则可以这样表示：

我们可以把它写成通用的表示形式：

其中 pi 是一个行向量，表示第 i 个基， aj 是一个列向量，表示第 j 个原始数据记录。实际上也就是做了一个向量矩阵化的操作。

上述分析给矩阵相乘找到了一种物理解释：两个矩阵相乘的意义是将右边矩阵中的每一列向量ai 变换到左边矩阵中以每一行行向量为基所表示的空间中去。也就是说一个矩阵可以表示一种线性变换。

2.4最大可分性

上面我们讨论了选择不同的基可以对同样一组数据给出不同的表示，如果基的数量少于向量本身的维数，则可以达到降维的效果。

但是我们还没回答一个最关键的问题：如何选择基才是最优的。或者说，如果我们有一组 N 维向量，现在要将其降到 K 维（K 小于 N），那么我们应该如何选择 K 个基才能最大程度保留原有的信息？

一种直观的看法是：希望投影后的投影值尽可能分散，因为如果重叠就会有样本消失。当然这个也可以从熵的角度进行理解，熵越大所含信息越多。

2.5方差

我们知道数值的分散程度，可以用数学上的方差来表述。一个变量的方差可以看做是每个元素与变量均值的差的平方和的均值，即：

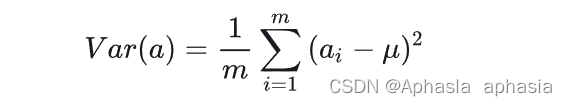
为了方便处理，我们将每个变量的均值都化为 0 ，因此方差可以直接用每个元素的平方和除以元素个数表示：

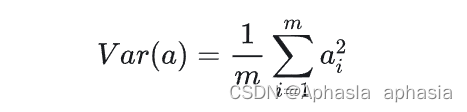
于是上面的问题被形式化表述为：寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。

2.6协方差

在一维空间中我们可以用方差来表示数据的分散程度。而对于高维数据，我们用协方差进行约束，协方差可以表示两个变量的相关性。为了让两个变量尽可能表示更多的原始信息，我们希望它们之间不存在线性相关性，因为相关性意味着两个变量不是完全独立，必然存在重复表示的信息。

协方差公式为：

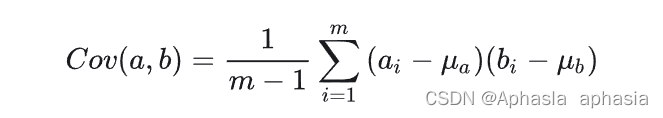
由于均值为 0，所以我们的协方差公式可以表示为：

当样本数较大时，不必在意其是 m 还是 m-1，为了方便计算，我们分母取 m。

当协方差为 0 时，表示两个变量线性不相关。为了让协方差为 0，我们选择第二个基时只能在与第一个基正交的方向上进行选择，因此最终选择的两个方向一定是正交的。

至此，我们得到了降维问题的优化目标：将一组 N 维向量降为 K 维，其目标是选择 K 个单位正交基，使得原始数据变换到这组基上后，各变量两两间协方差为 0，而变量方差则尽可能大（在正交的约束下，取最大的 K 个方差）。

2.7协方差矩阵

针对我们给出的优化目标，接下来我们将从数学的角度来给出优化目标。

我们看到，最终要达到的目的与变量内方差及变量间协方差有密切关系。因此我们希望能将两者统一表示，仔细观察发现，两者均可以表示为内积的形式，而内积又与矩阵相乘密切相关。于是我们有：

假设我们只有 a 和 b 两个变量，那么我们将它们按行组成矩阵 X：

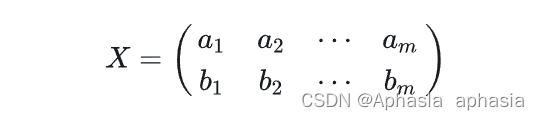
然后：

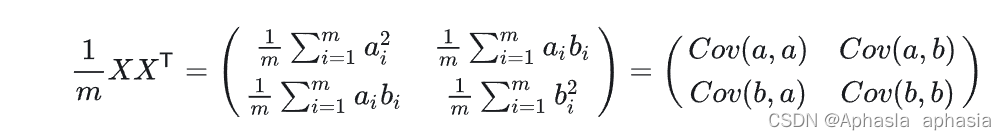
我们可以看到这个矩阵对角线上的分别是两个变量的方差，而其它元素是 a 和 b 的协方差。两者被统一到了一个矩阵里。

我们很容易被推广到一般情况：

设我们有 m 个 n 维数据记录，将其排列成矩阵Xmn ，设 ，则 C 是一个对称矩阵，其对角线分别对应各个变量的方差，而第 i 行 j 列和 j 行 i 列元素相同，表示 i 和 j 两个变量的协方差。

2.8矩阵对角化

根据我们的优化条件，我们需要将除对角线外的其它元素化为 0，并且在对角线上将元素按大小从上到下排列（变量方差尽可能大），这样我们就达到了优化目的。这样说可能还不是很明晰，我们进一步看下原矩阵与基变换后矩阵协方差矩阵的关系。

设原始数据矩阵 X 对应的协方差矩阵为 C，而 P 是一组基按行组成的矩阵，设 Y=PX，则 Y 为 X 对 P 做基变换后的数据。设 Y 的协方差矩阵为 D，我们推导一下 D 与 C 的关系：

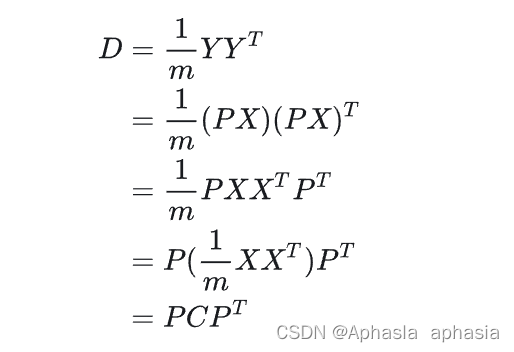
这样我们就看清楚了，我们要找的 P 是能让原始协方差矩阵对角化的 P。换句话说，优化目标变成了寻找一个矩阵 P，满足  是一个对角矩阵，并且对角元素按从大到小依次排列，那么 P 的前 K 行就是要寻找的基，用 P 的前 K 行组成的矩阵乘以 X 就使得 X 从 N 维降到了 K 维并满足上述优化条件。

至此，我们离 PCA 还有仅一步之遥，我们还需要完成对角化。

由上文知道，协方差矩阵 C 是一个是对称矩阵，在线性代数中实对称矩阵有一系列非常好的性质：

1. 实对称矩阵不同特征值对应的特征向量必然正交。
2. 设特征向量 � 重数为 r，则必然存在 r 个线性无关的特征向量对应于 � ，因此可以将这 r 个特征向量单位正交化。

由上面两条可知，一个 n 行 n 列的实对称矩阵一定可以找到 n 个单位正交特征向量，设这 n 个特征向量为 e1，e2......en ，我们将其按列组成矩阵： E=(e1，e2......en) 。

则对协方差矩阵 C 有如下结论：

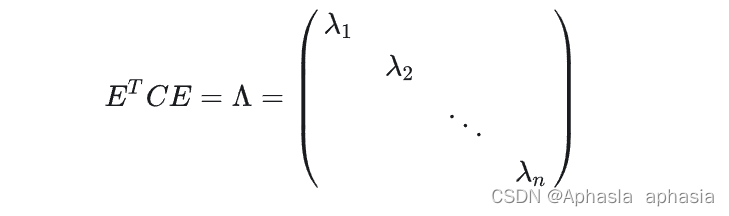
其中 Λ 为对角矩阵，其对角元素为各特征向量对应的特征值（可能有重复）。

到这里，我们发现我们已经找到了需要的矩阵 

P 是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是 C 的一个特征向量。如果设 P 按照 Λ 中特征值的从大到小，将特征向量从上到下排列，则用 P 的前 K 行组成的矩阵乘以原始数据矩阵 X，就得到了我们需要的降维后的数据矩阵 Y。

2.9拉格朗日乘子法

在叙述求协方差矩阵对角化时，我们给出希望变化后的变量有：变量间协方差为 0 且变量内方差尽可能大。然后我们通过实对称矩阵的性质给予了推导，此外我们还可以把它转换为最优化问题利用拉格朗日乘子法来给予推导。

我们知道样本点 Xi在基 w 下的坐标为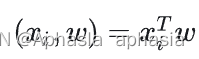，于是我们有方差：

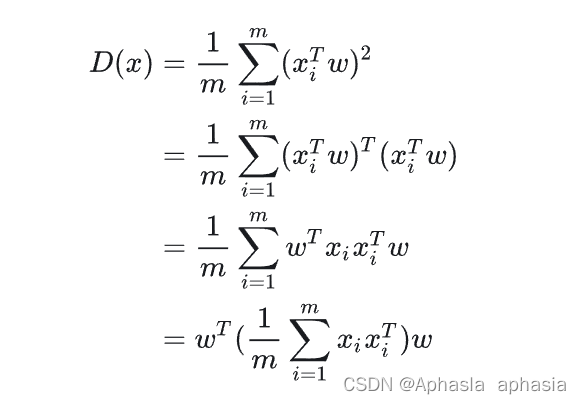
我们看到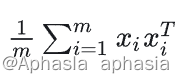就是原样本的协方差，我们另这个矩阵为 Λ ，于是我们有：

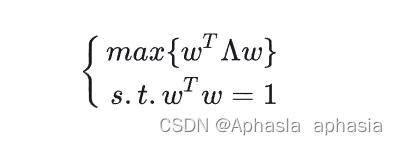
构造拉格朗日函数：

对 w 求导：

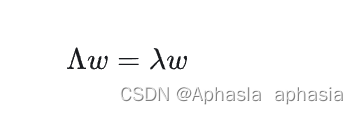
此时我们的方差为：

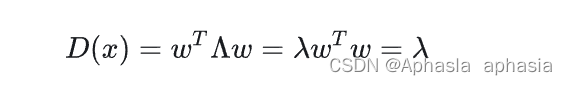
于是我们发现，x 投影后的方差就是协方差矩阵的特征值。我们要找到最大方差也就是协方差矩阵最大的特征值，最佳投影方向就是最大特征值所对应的特征向量，次佳就是第二大特征值对应的特征向量，以此类推。

至此我们完成了基于最大可分性的 PCA 数学证明

2.10最近重构性

以上的证明思路主要是基于最大可分性的思想，通过一条直线使得样本点投影到该直线上的方差最大。除此之外，我们还可以将其转换为线型回归问题，其目标是求解一个线性函数使得对应直线能够更好地拟合样本点集合。这就使得我们的优化目标从方差最大转化为平方误差最小，因为映射距离越短，丢失的信息也会越小。区别于最大可分性，这是从最近重构性的角度进行论证。

三、PCA的具体实现方法

3.1实现的步骤

设有 m 条 n 维数据。

1. 将原始数据按列组成 n 行 m 列矩阵 X；
2. 将 X 的每一行进行零均值化，即减去这一行的均值；
3. 求出协方差矩阵  ；
4. 求出协方差矩阵的特征值及对应的特征向量；
5. 将特征向量按对应特征值大小从上到下按行排列成矩阵，取前 k 行组成矩阵 P；
6. Y=PX 即为降维到 k 维后的数据。

3.2构建协方差矩阵

对于我们得到的一组数据，可以求出其样本均值：

样本方差：

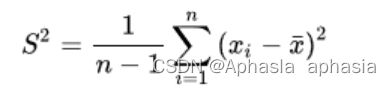
两个样本之间的协方差：

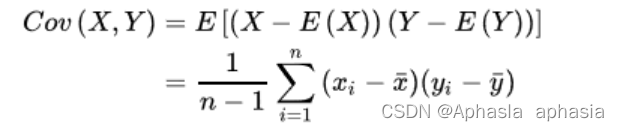
当协方差为0时，说明X和Y变量之间是线性无关的。

由所有的样本的列向量组成的矩阵X,根据可以得到两两数据之间的协方差矩阵：

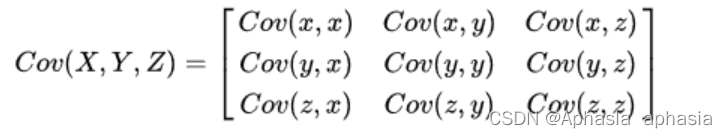
由矩阵知识可知，协方差矩阵为对称矩阵，对角线上为样本的方差，其他为两两变量之间的协方差。我们便可以利用对称矩阵的对角化将协方差化为0，实现变量间的线性无关，并且此时对角线上选取最大的K个方差即可。

3.3特征值和特征向量

根据协方差矩阵计算其特征值与特征向量，由线性代数我们知道，如果一个向量v是矩阵A的特征向量，将一定可以表示成下面的形式：

从而利用 |λE - A| = 0可解出矩阵的特征值，一个特征值便对应一组特征向量，特征向量之间是相互正交的。将所得到的特征向量对应其特征值从大到小排列，选出最大的k个向量单位化，便可作为PCA变换所需要的k个基向量，且方差最大。
通过数学方法可以证明，特征值λ即为降维后数据的方差，具体证明可以参照拉格朗日乘数法的最优化，在此不赘述。
 

3.4基向量的变换

X是一个mxn 的矩阵，它的每一个列向量都表示一个采样点上的数据 。Y 表示转换以后的新的数据集表示。 P是他们之间的线性转换，即计算向量内积。可表示为：

Y=PX
P便是由基向量组成的变换矩阵，经过线性转换，X的坐标便转换到新的基向量所决定的空间中的坐标Y,从几何上看，Y是X在新的空间中的投影。

经过基向量变换，即完成了数据的降维。

四、PC实现的实例分析

以这样一组二维数据为例

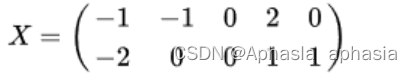
我们要把它降到一维，两组行向量的均值都为零，故不需要零均值中心化。

求协方差矩阵：

再根据所求的协方差矩阵计算其特征值与特征向量，求解得特征值为：

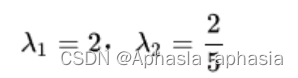
对应的特征向量为：

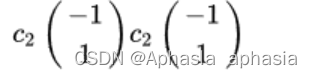
将特征向量单位化得到：

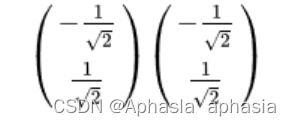
故基向量变换矩阵为：

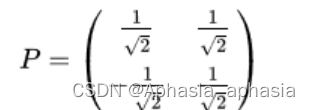
最后利用P与矩阵X做向量内积，便得到降维后的矩阵Y：

N维的数据矩阵也可以此类推，在得到k维降维后的向量之后，通常取2-3维作为主成分坐标，便可反映绝大部分的特征信息。

五、代码实现

5.1主体代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits

# 加载手写数字数据集
digits = load_digits()
X = digits.data
y = digits.target

# 绘制降维前的图像
fig, ax = plt.subplots(nrows=2, ncols=5, sharex=True, sharey=True, figsize=(10, 5))
ax = ax.flatten()
for i in range(10):
    img = X[y == i][0].reshape(8, 8)
    ax[i].imshow(img, cmap='Greys')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()

# PCA 的实现过程
mean_vec = np.mean(X, axis=0)
cov_mat = np.cov(X.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
sorted_idx = np.argsort(eig_vals)[::-1]
sorted_eig_vals = eig_vals[sorted_idx]
sorted_eig_vecs = eig_vecs[:, sorted_idx]
k = 2
projection_mat = sorted_eig_vecs[:, :k]
X_pca = X.dot(projection_mat)

# 绘制降维后的图像
colors = ['red', 'blue', 'green', 'purple', 'yellow', 'orange', 'pink', 'cyan', 'gray', 'brown']
plt.figure(figsize=(10, 8))
for i in range(len(colors)):
    plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], c=colors[i], label=str(i), edgecolor='k')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(title='Digit')
plt.title('PCA on MNIST Dataset')
plt.show()
plt.show()

5.2代码分析

首先我们使用 load_digits 函数加载手写数字数据集，将特征存储在变量 X 中，将标签存储在变量 y 中。

然后，我绘制降维前的图像。具体地，我们选取每个数字类别中的第一个样本，将其转换成 8x8 的图像并展示出来。

接着，我按照 PCA 的实现过程对数据进行降维操作。具体地，我首先计算样本的均值向量和协方差矩阵，然后对协方差矩阵进行特征值分解，得到特征值和特征向量。接着，我们将特征向量按照对应的特征值大小排序，并选取前两个特征向量组成投影矩阵。最后，我将原始数据点乘以投影矩阵，得到降维后的数据 X_pca。

最后，我们使用 matplotlib 绘制降维后的图像。我们根据每个样本的标签将其在降维空间中的坐标进行着色，并绘制出来。

5.3代码的输出

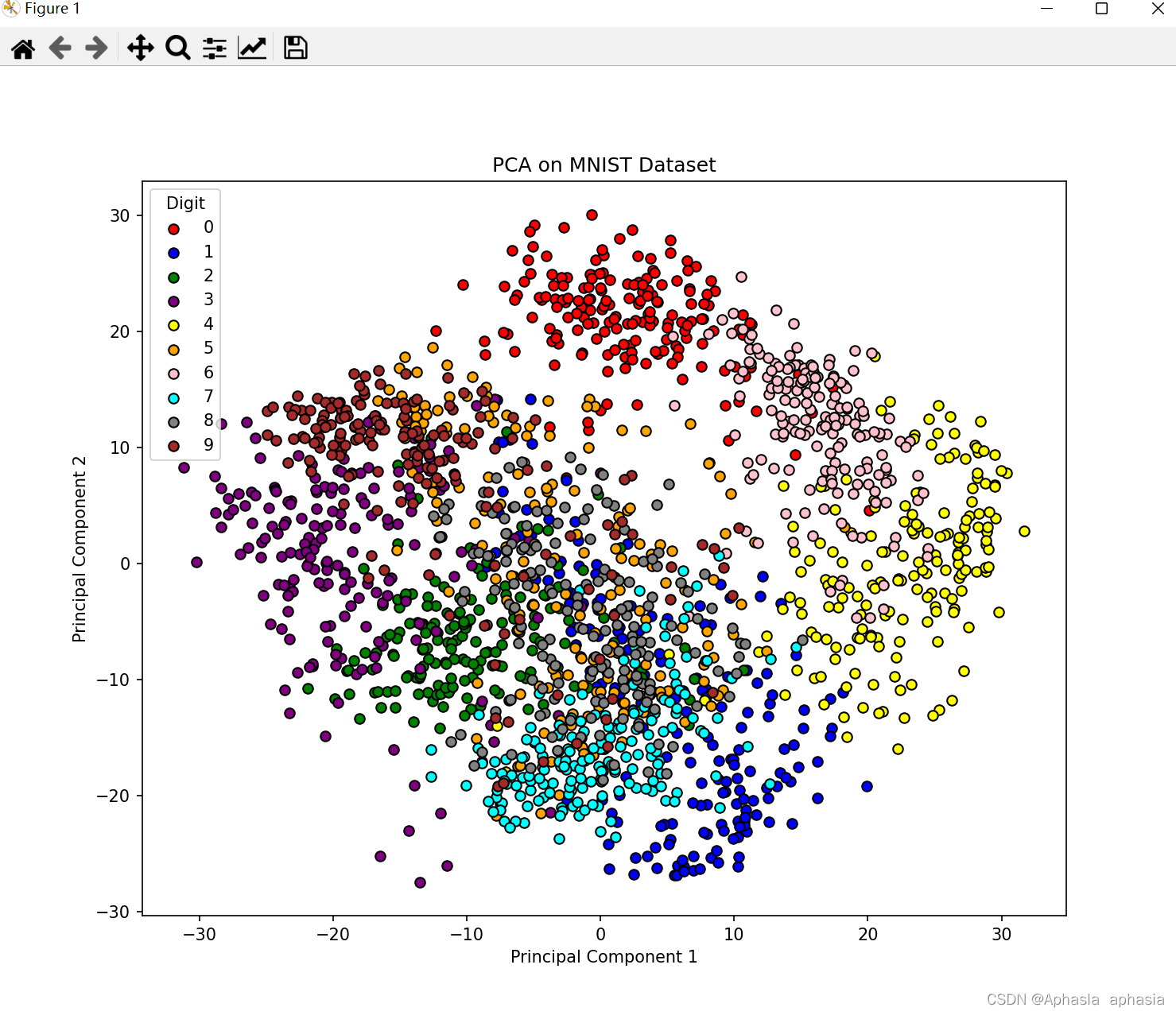
六、总结

6.1PCA的性质

需要注意的是，PCA 是基于线性变换的降维方法，在某些情况下可能无法捕捉到非线性的数据结构。对于非线性数据，可以考虑使用核主成分分析（Kernel PCA）等非线性降维方法。

1. 最大可分性：PCA 旨在通过选择投影方向来最大程度地保留原始数据的方差。这意味着第一个主成分将包含数据中的最大方差，第二个主成分将包含数据中的次大方差，以此类推。通过选择前k个主成分，可以保留数据中大部分的方差，从而最大程度地保留原始数据的信息。

2. 无关性：PCA 通过选择正交的主成分来表示数据。这意味着每个主成分与其他主成分是不相关的。这种无关性使得 PCA 在降维过程中能够最大限度地减少特征之间的冗余。

3. 数据恢复：在 PCA 中，我们可以使用选定的主成分将降维后的数据映射回原始高维空间。这意味着我们可以通过反向变换来恢复降维后的数据，尽可能地接近原始数据。

4. 特征重要性排序：PCA 的特征值表示了对应特征向量所解释的方差大小。较大的特征值表示了对应主成分所包含的信息量更多。因此，我们可以根据特征值的大小来评估每个主成分的重要性。通过选择具有最大特征值的主成分，我们可以选择保留最多信息的投影方向。

5. 数据可视化：PCA 可以帮助我们将高维数据投影到低维空间中，通常是二维或三维空间。这使得我们能够更容易地可视化高维数据，并在图形上观察数据之间的模式和关系。

6.2 零均值化的注意使用

当对训练集进行 PCA 降维时，也需要对验证集、测试集执行同样的降维。而对验证集、测试集执行零均值化操作时，均值必须从训练集计算而来，不能使用验证集或者测试集的中心向量。

其原因也很简单，因为我们的训练集时可观测到的数据，测试集不可观测所以不会知道其均值，而验证集再大部分情况下是在处理完数据后再从训练集中分离出来，一般不会单独处理。如果真的是单独处理了，不能独自求均值的原因是和测试集一样。

另外我们也需要保证一致性，我们拿训练集训练出来的模型用来预测测试集的前提假设就是两者是独立同分布的，如果不能保证一致性的话，会出现 Variance Shift 的问题。