机器学习全解 - PCA主成分分析（含算法讲解，公式全解，手写代码实现，调包实现）

本文链接：https://blog.csdn.net/qq_51222843/article/details/138864327

1. PCA主成分分析

1.1 降维

降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。

通俗来讲就是将一个样本中的多个特征进行筛选，保留最重要的特征，能够快速处理数据，为数据样本提供一个更好的解释效果。

1.2 PCA算法

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

实际上PCA算法的本质就是将样本的特征进行重新构造。如下图所示，这里有两个样本点A，B，每个样本拥有两个特征，如左图所示每个特征体现在坐标轴之上。PCA算法的实质就是重现构造特征，并且新的特征能够最大程度的反应原始数据之间特征的不同。

如右图所示，我们为这两个样本构造一个新的坐标轴l，A与B在l上的投影就是降维得到的新特征。怎样才能保证原有数据特征之间的特点呢？

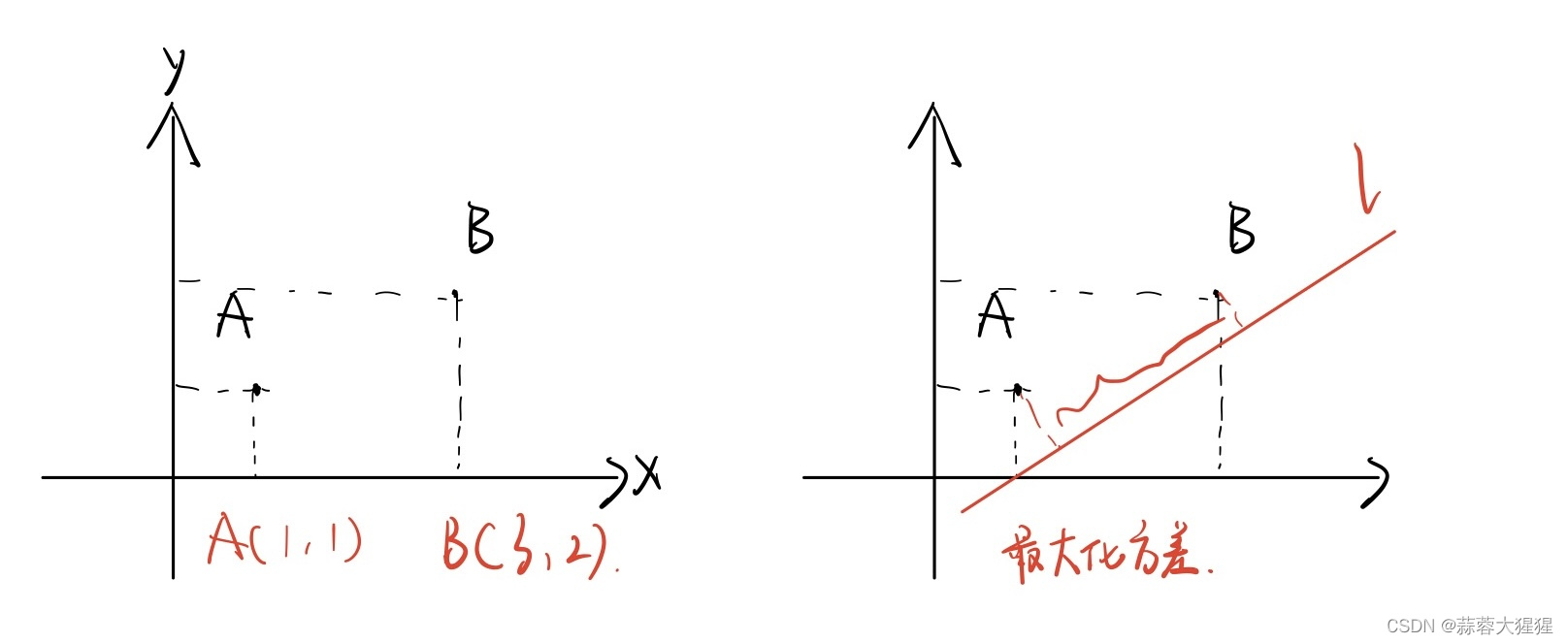
答案就是最大化方差。

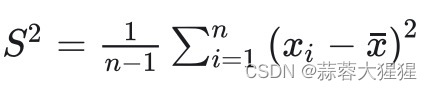
脑补一下怎样去区分数据，数据集A平均数为100，数据集C平均数为1，我们可以很好的去区分数据集A中的数据是大于数据集C的，但如果A&C的平均数各是60.0与60.1呢，最大化方差的效果就是尽可能使样本不仅保留原始效果还将样本间的可辨别性增强，让他们尽可能分散。

但现在又出现了新的问题，如果数据降维这么轻松找到方差最大的方向，那降至二维就是找方差最大的两个方向么？

与之前相同，首先我们希望找到一个方向使得投影后方差最大，这样就完成了第一个方向的选择，继而我们选择第二个投影方向。

如果我们还是单纯只选择方差最大的方向，很明显，这个方向与第一个方向应该是“几乎重合在一起”，显然这样的维度是没有用的，因此，应该有其他约束条件。从直观上说，让两个字段尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，因为相关性意味着两个字段不是完全独立，必然存在重复表示的信息。

所以每个方向之间应该是不相关的，数学上我们使用协方差来衡量相关性

假设我们现在有一组数据：

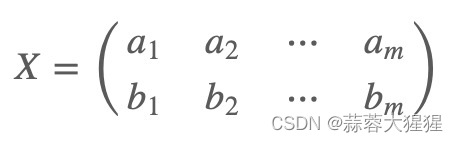
这是这组数据的协方差矩阵：

一边对角线就是协方差，另一边的对角线为方差，上述我们所说我们需要协方差为0，OK很简单直接将代表协方差的数值设置为0即可。为一个对角线矩阵。

这代表变换后的数据样本协方差为0.

设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系：

根据上述所推导，D为一个对角线矩阵，所以我们问题转换为求解P使得原数据协方差矩阵转换为对角线矩阵，也就是老生常谈的矩阵对角化。

数学家真的令人敬佩，特征向量与特征值就派上了用场。

其中，特征向量表示表示新的坐标轴，特征值表示这些主成分方向上投影数据较大的方差。

1.3 基于特征值分解协方差矩阵实现PCA算法

总结一下算法：

输入：数据集，需要降到k维。

1) 去平均值(即去中心化)，即每一位特征减去各自的平均值。

2) 计算协方差矩阵，这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。

3) 用特征值分解方法求协方差矩阵的特征值与特征向量。

4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。

5) 将数据转换到k个特征向量构建的新空间中，即Y=PX。

看着抽象的很，直接上算法公式：

设有m条n维数据。

1）将原始数据按列组成n行m列矩阵X

2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值

3）求出协方差矩阵C=1/m * X *X𝖳

4）求出协方差矩阵的特征值及对应的特征向量

5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P

6）Y=PX即为降维到k维后的数据

2. 手写代码实现

#PCA
import numpy as np
dataset = np.mat([[1,2,3],[4,5,6],[7,8,9],[1,4,6],[7,0,2],[9,10,5],[1,2,2]])

def pca(datamat,topNfeat): #topNfeat保留多少个特征
    meanVals = np.mean(datamat,axis=0)
    meanRemoved = datamat - meanVals #去除平均值
    covMat = np.cov(meanRemoved,rowvar=0) #计算协方差矩阵
    eigVals,eigVects = np.linalg.eig(np.mat(covMat)) #获取特征值与特征向量
    eigValInd = np.argsort(eigVals) #特征值从小到大排列
    eigValInd = eigValInd[:-(topNfeat+1):-1] #保留最上面N个特征向量
    redEigVects = eigVects[:,eigValInd] #转移构建的新空间 从大到小特征值所对应的特征向量
    lowDDataMat = meanRemoved * redEigVects#在特征向量上的投影

    return lowDDataMat

结果显示：

3. 调包实现

from sklearn.decomposition import PCA
import numpy as np
X = np.array([[1,2,3],[4,5,6],[7,8,9],[1,4,6],[7,0,2],[9,10,5],[1,2,2]])
pca=PCA(n_components=2)
pca.fit(X)
print(pca.transform(X))

结果显示与我们的手写代码一模一样。