SVM算法

一、定义输⼊数据

假设给定⼀个特征空间上的训练集为：T = {(x , y ),(x , y )…,(x , y )}
x i∈ R , y ∈ {+1, −1},i = 1, 2, …, N.其中，(x ,y )称为样本点。x 为第i个实例（样本），
y 为的x 标记：

• 当y =1时，为x 正例
• 当y =-1时，为x 负例

二、线性可分⽀持向量机

给定了上⾯提出的线性可分训练数据集，通过间隔最⼤化得到分离超平⾯为 :y(x) = w Φ(x) + b
相应的分类决策函数为： $f(x)=sign(w^T\varphi (x)+b)$以上决策函数就称为线性可分⽀持向量机。
$\varphi (x)$这是某个确定的特征空间转换函数，它的作⽤是将x映射到更⾼的维度，它有⼀个
以后我们经常会⻅到的专有称号”核函数“。

⽐如我们看到的特征有2个： x1,x2,组成最先⻅到的线性函数可以是:$w_1{x}_1+w_2{x}_2$但也许这两个特征并不能很好地描述数据，于是我们进⾏维度的转化，变成了:$w_1{x}_1+w_2{x}_2+w_3{x}_1{x}_2+w_4{x}_1^2+w_5{x}_2^2$,于是我们多了三个特征。⽽这个就是笼统地描述x的映射的。 最简单直接的就是：$\varphi (x=x)$

以上就是线性可分⽀持向量机的模型表达式。我们要去求出这样⼀个模型，或者说
这样⼀个超平⾯y(x),它能够最优地分离两个集合。其实也就是我们要去求⼀组参数（w,b),使其构建的超平⾯函数能够最优地分离两个集合。
如下就是⼀个最优超平⾯：

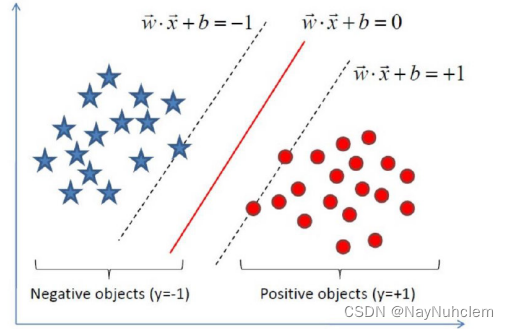
也可以如下：

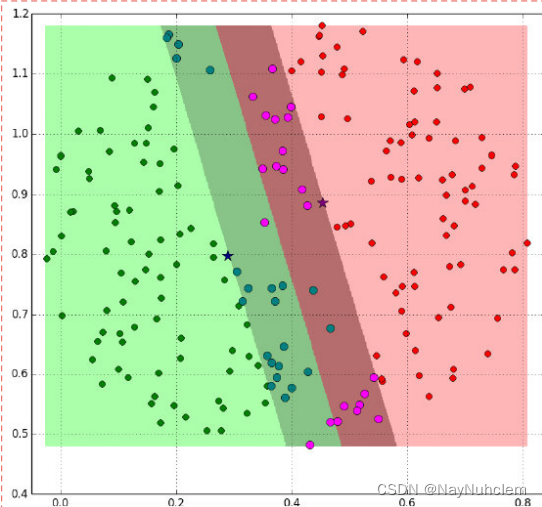
阴影部分是⼀个“过渡带”，“过渡带”的边界是集合中离超平⾯最近的样本点落在的
地⽅。

三、SVM的计算过程与算法步骤

3.1 推导⽬标函数

我们知道了⽀持向量机是个什么东⻄了。现在我们要去寻找这个⽀持向量机，也就
是寻找⼀个最优的超平⾯。
于是我们要建⽴⼀个⽬标函数。那么如何建⽴呢？
再来看⼀下我们的超平⾯表达式： y(x) = w Φ(x) + b
为了⽅便我们让：Φ(x) = x
则在样本空间中，划分超平⾯可通过如下线性⽅程来描述：w x + b = 0

• 我们知道 $w=(w1,w2,...wd)$为法向量，决定了超平⾯的⽅向；
• b为位移项，决定了超平⾯和原点之间的距离。
• 显然，划分超平⾯可被法向量w和位移b确定，我们把其记为（w,b）.样本空间中任意点x到超平⾯（w,b）的距离可写成$r=\frac{w^T+b}{|w|}$

假设超平⾯（w, b）能将训练样本正确分类，即对于$(x_i,y_i)\in D$

• 若$y_i=+1$,则有$w^T{x}_i+b>0$
• 若$y_i=-1$,则有$w^T{x}_i+b<0$

令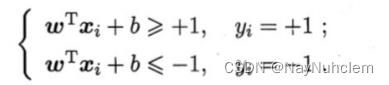

如图所示，距离超平⾯最近的⼏个训练样本点使上式等号成⽴，他们被称为“⽀持
向量"，
两个异类⽀持向量到超平⾯的距离之和为:$r=\frac{2}{||w||}$，它被称为“”间隔“”。

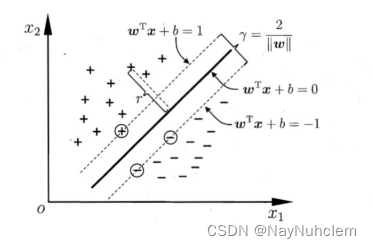
欲找到具有最⼤间隔的划分超平⾯，也就是要找到能满⾜下式中约束的参数w和b，使得 r 最⼤。

显然，为了最⼤化间隔，仅需要最⼤化${\left|\left|w\right|\right|}^{-1}$ ，这等价于最⼩化 ${\left|\left|w\right|\right|}^2$。于是
上式可以重写为：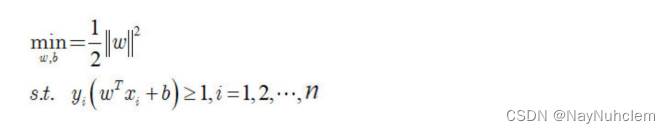
这就是⽀持向量机的基本型。

3.2 目标函数的求解

到这⼀步，终于把⽬标函数给建⽴起来了。
那么下⼀步⾃然是去求⽬标函数的最优值.
因为⽬标函数带有⼀个约束条件，所以我们可以⽤拉格朗⽇乘⼦法求解。

3.2.1 拉格朗日乘子法

拉格朗⽇乘⼦法 (Lagrange multipliers)是⼀种寻找多元函数在⼀组约束下的极值的⽅法.
通过引⼊拉格朗⽇乘⼦，可将有 d 个变量与 k 个约束条件的最优化问题转化为具有d + k 个变量的⽆约束优化问题求解。
经过朗格朗⽇乘⼦法，我们可以把⽬标函数转换为：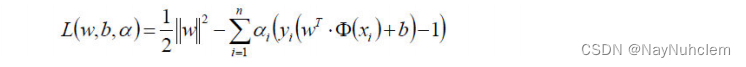
然后我们令：
容易验证，当某个约束条件不满⾜时，例如$y_i(w^T{x}_i+b)<1$，那么显然有 θ(w) = ∞ （只要令 αi =∞ 即可）。⽽当所有约束条件都满⾜时，则有$\theta (w)=\frac{1}{2}{\left|\left|w\right|\right|}^2$，亦即最初要 最⼩化的量。
因此，在要求约束条件得到满⾜的情况下最⼩化$\frac{1}{2}{\left|\left|w\right|\right|}^2$，实际上等价于直接最⼩化 θ(w)（当然， 这⾥也有约束条件， 就是 α ≥ 0, i = 1, …, n），因为如果约束条件没有得 到满⾜， θ(w) 会等于⽆穷⼤，⾃然不会是我们所要求的最⼩值。
具体写出来，⽬标函数变成了：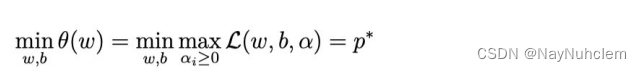
这⾥⽤ p* 表示这个问题的最优值，且和最初的问题是等价的。如果直接求解，那么⼀上来便得⾯对 w 和 b 两个参数，⽽ α ⼜是不等式约束，这个求解过程不好做。
此时，我们可以借助对偶问题进⾏求解。

3.2.2 对偶问题

因为我们在上⾯求解的过程中，直接求解 w 和 b 两个参数不⽅便，所以想办法转换为对偶问题。
我们要将其转换为对偶问题，变成极⼤极⼩值问题：
如何获取对偶函数？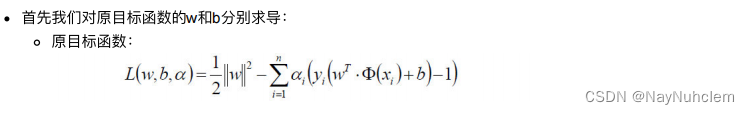

3.2.3 整体流程确定

四、SVM的损失函数

在SVM中，我们主要讨论三种损失函数：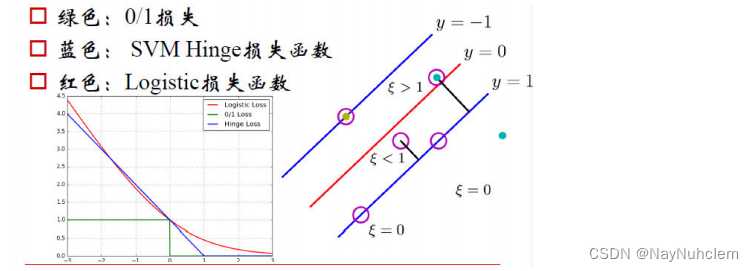

• 绿色：0/1损失
  • 当正例的点落在y=0这个超平⾯的下边，说明是分类正确，⽆论距离超平⾯所远多近，误差都是0.
  • 当这个正例的样本点落在y=0的上⽅的时候，说明分类错误，⽆论距离多 远多近，误差都为1.
  • 图像就是上图绿⾊线。
• 蓝色：SVM Hinge损失函数
  • 当⼀个正例的点落在y=1的直线上，距离超平⾯⻓度1，那么1-ξ=1，ξ=0，也就是说误差为0；
  • 当它落在距离超平⾯0.5的地⽅，1-ξ=0.5，ξ=0.5，也就是说误差为0.5；
  • 当它落在y=0上的时候，距离为0，1-ξ=0，ξ=1，误差为1；
  • 当这个点落在了y=0的上⽅，被误分到了负例中，距离算出来应该是负的，⽐如-0.5，那么1-ξ=-0.5，ξ=1.5.误差为1.5.
  • 以此类推，画在⼆维坐标上就是上图中蓝⾊那根线了。
• 红色：Logistic损失函数
  • 损失函数的公式为：$ln(1+e^{-yi})$
  • 当yi=0 时，损失等于ln2,这样真丑，所以我们给这个损失函数除以ln2.
  • 这样到yi=0时，损失为1，即损失函数过（0，1）点
  • 即上图中的红⾊线。

五、SVM的核方法

核函数并不是SVM特有的，核函数可以和其他算法也进⾏结合，只是核函数与SVM结合的优势⾮常⼤。

1 什么是核函数

1.1 核函数概念

核函数，是将原始输⼊空间映射到新的特征空间，从⽽，使得原本线性不可分的样本可能在核空间可分。
下图所示的两类数据，分别分布为两个圆圈的形状，这样的数据本身就是线性不可分的，此时该如何把这两类数据分开呢?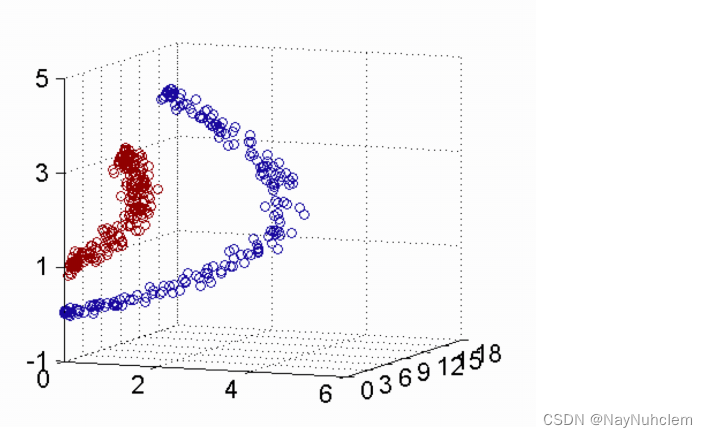

• 假设X是输⼊空间
• H是特征空间
• 存在⼀个映射ϕ使得X中的点x能够计算得到H空间中的点h
• 对于所有的X中的点都成⽴：$h=\varphi (x)$
  若x，z是X空间中的点，函数k(x,z)满⾜下述条件，那么都成⽴，则称k为核函数，⽽ϕ为映射函数：
  $$k(x,z)=\varphi (x)\bullet \varphi (z)$$

1.2 核函数举例

1.2.1 核⽅法举例

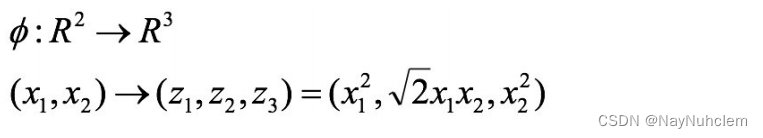
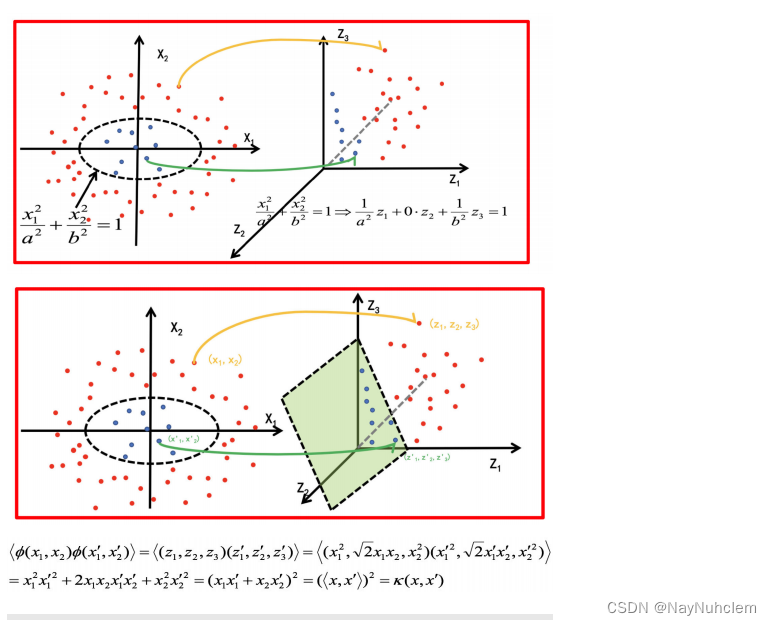
经过上⾯公式，具体变换过过程为：

2 常见核函数

1.多项核中，d=1时，退化为线性核；
2.⾼斯核亦称为RBF核。

• 线性核和多项式核：
  • 这两种核的作⽤也是⾸先在属性空间中找到⼀些点，把这些点当做base，核函数的作⽤就是找与该点距离和⻆度满⾜某种关系的样本点。
  • 当样本点与该点的夹⻆近乎垂直时，两个样本的欧式⻓度必须⾮常⻓才能保证满⾜线性核函数⼤于0；⽽当样本点与base点的⽅向相同时，⻓度就不必很⻓；⽽当⽅向相反时，核函数值就是负的，被判为反类。即，它在空间上划分出⼀个梭形，按照梭形来进⾏正反类划分。
• RBF核：
  • ⾼斯核函数就是在属性空间中找到⼀些点，这些点可以是也可以不是样本点，把这些点当做base，以这些base为圆⼼向外扩展，扩展半径即为带宽，即可划分数据。
  • 换句话说，在属性空间中找到⼀些超圆，⽤这些超圆来判定正反类。
• Sigmoid核：
  • 同样地是定义⼀些base，
  • 核函数就是将线性核函数经过⼀个tanh函数进⾏处理，把值域限制在了-1到1上。
• 总之，都是在定义距离，⼤于该距离，判为正，⼩于该距离，判为负。⾄于选
  择哪⼀种核函数，要根据具体的样本分布情况来确定。

⼀般有如下指导规则：
1） 如果Feature的数量很⼤，甚⾄和样本数量差不多时，往往线性可分，这时选⽤LR或者线性核Linear；
2） 如果Feature的数量很⼩，样本数量正常，不算多也不算少，这时选⽤RBF核；
3） 如果Feature的数量很⼩，⽽样本的数量很⼤，这时⼿动添加⼀些Feature，使得线性可分，然后选⽤LR或者线性核Linear；
4） 多项式核⼀般很少使⽤，效率不⾼，结果也不优于RBF；
5） Linear核参数少，速度快；RBF核参数多，分类结果⾮常依赖于参数，需要交叉验证或⽹格搜索最佳参数，⽐较耗时；
6）应⽤最⼴的应该就是RBF核，⽆论是⼩样本还是⼤样本，⾼维还是低维等情况，RBF核函数均适⽤。

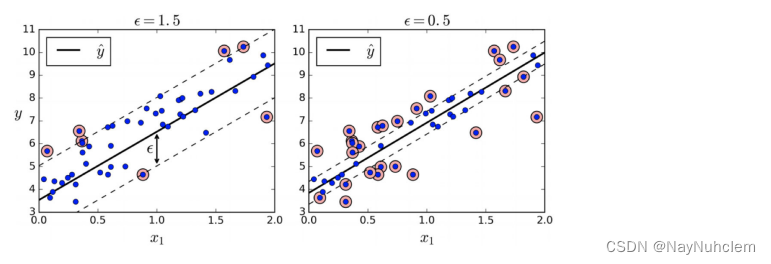
六、SVM回归

SVM回归是让尽可能多的实例位于预测线上，同时限制间隔违例（也就是不在预测线距上的实例）。

线距的宽度由超参数ε控制。