★★★ 本文源自AlStudio社区精品项目,【点击此处】查看更多精品内容 >>>
1. 项目简介
该项目是基于飞桨paddlepaddle框架复现论文Reduced-order Model for Fluid Flows via Neural Ordinary Differential Equations。该项目的内容是对时间系数的模拟来实现降阶系统(ROM)对全阶系统(FOM)的重构,具体实现思路如下:
- 使用大涡模拟(LES)获取300组全阶系统的模拟数据,流经圆柱的冯卡门涡街数据集 - 飞桨AI Studio (baidu.com)
- 使用本征正交分解(
POD)对全阶系统数据分解,选取前8个POD模式 - 拟设一个分解,假定原时空系统可有分解:时空系数(矩阵)= 时间系数(矩阵) x 空间系数(矩阵)
- 将时间系数提取出来,输入到一个包含神经微分方程节点的变分自编码器(
VAE)中,编码器用于提取关键特征,解码器用于还原时间系数 - 利用还原的参数和原有参数进行比较并且重构时空系统
2. 物理场描述
二维圆柱绕流的流动控制方程(NS方程)的LES求解方程其可写成如下
∂
ρ
∂
t
+
ρ
u
i
∂
x
i
=
0
(2.1)
\frac{\partial \rho}{\partial t}+\frac{\rho u_i}{\partial x_i}=0 \tag{2.1}
∂t∂ρ+∂xiρui=0(2.1)
∂
ρ
u
i
∂
t
+
∂
(
u
i
u
j
)
∂
x
j
=
∂
∂
x
j
[
ρ
v
(
∂
u
j
∂
x
i
+
∂
u
i
∂
x
j
)
−
2
3
ρ
v
∂
u
k
∂
x
k
δ
i
j
−
ρ
τ
i
j
s
g
s
]
−
∂
ρ
∂
x
i
+
ρ
g
i
(2.2)
\frac{\partial \rho u_i}{\partial t}+\frac{\partial (u_i u_j )}{\partial x_j}=\frac{\partial}{\partial x_j}[\rho v(\frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j})-\frac{2}{3}\rho v \frac{\partial u_k}{\partial x_k}\delta_{ij}-\rho \tau_{ij}^{sgs}]-\frac{\partial \rho}{\partial x_i}+\rho g_i \tag{2.2}
∂t∂ρui+∂xj∂(uiuj)=∂xj∂[ρv(∂xi∂uj+∂xj∂ui)−32ρv∂xk∂ukδij−ρτijsgs]−∂xi∂ρ+ρgi(2.2)
方程(2.1)为连续性方程,方程(2.2)为动量方程,
u
u
u表示速度,
ρ
\rho
ρ表示流体密度,
v
v
v表示动态粘度,使用PIMPLE算法对这些方程进行数值求解,求得速度的
x
x
x和
y
y
y分量(Re=240,t=100)如下所示

3. POD/PCA原理
注意:数据的方差代表了包含的信息量
本征正交分解(以下均称为POD)又称主成分分析(PCA),是一种源于矢量数据统计分析的方法,广泛应用于数据降维,流场分析等,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析就属于这类降维算法。
POD/PCA的主要思想和直观解释是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第一,二个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。
数学模型与求解: 设总体
x
=
(
x
1
,
x
2
,
.
.
.
,
x
p
)
T
x=(x_1, x_2, ..., x_p)^T
x=(x1,x2,...,xp)T,是
p
p
p元总体,
E
(
x
)
=
μ
E(x)=\mu
E(x)=μ,
V
a
r
(
x
)
=
Σ
=
(
σ
i
j
)
Var(x)=\Sigma=(\sigma_{ij})
Var(x)=Σ=(σij),目的是将这
p
p
p个指标综合成少数几个指标,且要求这些新指标既尽可能地反映原来
p
p
p个指标所提供地信息,彼此之间又互不相关。首先考虑将多维变量
x
x
x的各个指标综合成一维指标
y
1
y_1
y1,最直白的方法是将其取为原来
p
p
p个指标的线性组合,即设
u
=
(
u
1
,
u
2
,
.
.
.
,
u
p
)
T
u=(u_1, u_2, ..., u_p)^T
u=(u1,u2,...,up)T为待定的单位常数向量,令
y
1
=
u
1
x
1
+
u
2
x
2
+
.
.
.
+
u
p
x
p
=
u
T
x
(3.1)
y_1=u_1x_1+u_2x_2+...+u_px_p=u^Tx \tag{3.1}
y1=u1x1+u2x2+...+upxp=uTx(3.1)
希望选取合适的
u
u
u是
y
1
y_1
y1能尽可能多地反映
x
x
x地信息。由于信息量与方差成正比,因此可以使用
y
1
y_1
y1的方差来度量其所提供的
x
x
x信息量的多少。根据计算可以得到
V
a
r
(
y
1
)
=
u
T
Σ
u
Var(y_1)=u^T\Sigma u
Var(y1)=uTΣu,设
Σ
\Sigma
Σ的特征值为
λ
1
⩾
λ
2
⩾
.
.
.
⩾
λ
p
⩾
0
\lambda_1\geqslant \lambda_2\geqslant ...\geqslant\lambda_p\geqslant 0
λ1⩾λ2⩾...⩾λp⩾0,对应的特征向量为
a
1
,
a
2
,
.
.
.
,
a
p
a_1, a_2, ..., a_p
a1,a2,...,ap,对第
k
k
k个主成分
y
k
y_k
yk,数学模型可以记作
max
V
a
r
(
y
k
)
=
u
T
Σ
u
s
.
t
.
u
T
u
=
1
u
T
a
i
=
0
(
i
=
1
,
2
,
.
.
.
,
k
−
1
)
(3.2)
\begin{aligned} \max \quad &Var(y_k)=u^T\Sigma u \\ s.t. \quad &u^Tu=1 \\ \quad &u^Ta_i=0\quad (i=1, 2, ..., k-1)\\ \end{aligned} \tag{3.2}
maxs.t.Var(yk)=uTΣuuTu=1uTai=0(i=1,2,...,k−1)(3.2)
通过拉格朗日乘子法可以求得
u
u
u在
u
=
a
k
u=a_k
u=ak处取得最大值
λ
k
\lambda_k
λk。通过定义降维后数据包含的信息占原始数据信息的比重来确定降维后的维度
r
r
r,也就是根据特征值的贡献率来选取前
r
r
r个最大的特征向量,即定义一个比重阈值
a
∈
(
0
,
1
)
a\in (0,1)
a∈(0,1),使得
Σ
i
=
1
r
λ
i
Σ
i
=
1
p
λ
i
≥
a
(3.3)
\frac{\Sigma_{i=1}^r\lambda_i}{\Sigma_{i=1}^p\lambda_i} \geq a \tag{3.3}
Σi=1pλiΣi=1rλi≥a(3.3)
具体步骤可以概括为:通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的r个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中,实现数据特征的降维。由于得到协方差矩阵的特征值特征向量有两种方法:特征值分解协方差矩阵、奇异值分解协方差矩阵,所以PCA算法有两种实现方法:基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法(如果想深入继续学习,推荐哔哩哔哩PCA学习视频)。
4. 速度场的POD分解
- 使用流动的雷诺分解计算速度的波动分量:
u = u ˉ + u ‘ (4.1) u=\bar{u}+u^` \tag{4.1} u=uˉ+u‘(4.1)
u ˉ \bar{u} uˉ是FOM模型给出的解的时间平均值。 - 定义矩阵Y为以下形式组合:
Y = [ u x ‘ ( x 1 , y 1 , t 1 ) u y ‘ ( x N x , y N y , t N t ) . . . . . . u x ‘ ( x 1 , y 1 , t 1 ) u y ‘ ( x N x , y N y , t N t ) ] ∈ R N t × ( 2 × N x × N y ) (4.2) Y= \begin{bmatrix} u_x^`(x_1,y_1,t_1) & u_y^`(x_{N_x},y_{N_y},t_{N_t}) \\ ... & ... \\ u_x^`(x_1,y_1,t_1) & u_y^`(x_{N_x},y_{N_y},t_{N_t}) \end{bmatrix}\in R^{N_t \times (2\times N_x \times N_y)} \tag{4.2} Y= ux‘(x1,y1,t1)...ux‘(x1,y1,t1)uy‘(xNx,yNy,tNt)...uy‘(xNx,yNy,tNt) ∈RNt×(2×Nx×Ny)(4.2) - 建立相关矩阵
K
K
K并计算其特征向量
a
j
a_j
aj
K = Y Y T (4.3) K=YY^T \tag{4.3} K=YYT(4.3)
K a j = λ j a j (4.4) Ka_j=\lambda_j a_j \tag{4.4} Kaj=λjaj(4.4) - 选择模型的降维:较大的特征值与动力系统的主要特征直接相关,而较小的特征值则与动力行为的扰动相关。为新基础选择成分的标准是使用实现所需回收百分比所需的最小数量的成分N来最大化相对信息内容
I ( N ) = Σ i = 1 N λ i Σ i = 1 N t λ i (4.5) I(N)=\frac{\Sigma_{i=1}^N\lambda_i}{\Sigma_{i=1}^{N_t}\lambda_i} \tag{4.5} I(N)=Σi=1NtλiΣi=1Nλi(4.5) - 用降维空间中的时间系数和POD的一个假设分解来计算空间模式
u ‘ = Σ i = 1 N α i ( t ) Ψ i ( x ) Ψ i ( x ) = 1 λ i Σ j = 1 N α i ( y j ) u ‘ ( t j ) (4.6) \begin{aligned} &u^`=\Sigma_{i=1}^{N}\alpha_i(t) \Psi_i(x) \end{aligned} \\ \Psi_i(x)=\frac{1}{\lambda_i}\Sigma_{j=1}^N \alpha_i(y_j)u^`(t_j)\tag{4.6} u‘=Σi=1Nαi(t)Ψi(x)Ψi(x)=λi1Σj=1Nαi(yj)u‘(tj)(4.6)
Ψ i ( x ) , α ( t ) \Psi_i(x),\alpha(t) Ψi(x),α(t)分别为空间系数和时间系数。
5. Neural ODE介绍
神经常微分方程是利用数据驱动结合微分方程数值解来构建合适的微分方程模型。对一阶常微分方程
d
h
(
t
)
d
t
=
f
(
h
t
,
t
)
(5.1)
\frac{dh(t)}{dt}=f(h_t,t)\tag{5.1}
dtdh(t)=f(ht,t)(5.1)
其解应为
h
t
2
=
h
t
1
+
∫
t
1
t
2
f
(
h
t
,
t
)
d
t
(5.2)
h_{t_2}=h_{t_1}+\int_{t_1}^{t_2}{f(h_t, t)dt} \tag{5.2}
ht2=ht1+∫t1t2f(ht,t)dt(5.2)
通过积分中值定理可知,上式可简化为
h
t
2
=
h
t
1
+
f
(
h
ξ
,
θ
)
Δ
t
,
Δ
t
=
t
2
−
t
1
,
ξ
∈
[
t
1
,
t
2
]
(5.3)
h_{t_2}=h_{t_1}+{f(h_{\xi}, \theta)\Delta t},\quad \Delta t = t_2 - t_1, \quad \xi \in [t_1, t_2] \tag{5.3}
ht2=ht1+f(hξ,θ)Δt,Δt=t2−t1,ξ∈[t1,t2](5.3)
微分方程数值解是通过数值手段来构建平均增量
f
(
h
ξ
,
θ
)
f(h_{\xi}, \theta)
f(hξ,θ)来求解已知的微分方程模型,以经典四阶龙格-库塔方法为例
h
t
n
+
1
=
h
t
n
+
k
1
+
2
k
2
+
2
k
3
+
k
4
6
Δ
t
k
1
=
f
(
h
t
n
,
t
n
)
k
i
+
1
=
f
(
h
t
n
+
Δ
t
2
k
i
,
t
n
+
Δ
t
2
)
i
=
1
,
2
k
4
=
f
(
h
t
n
+
Δ
t
k
3
,
t
n
+
Δ
t
)
(5.4)
\begin{aligned} &h_{t_{n+1}}=h_{t_n}+\frac{k_1 + 2k_2 + 2k_3 + k_4}{6}\Delta t \\ &k_1=f(h_{t_n},t_n) \\ &k_{i+1}=f(h_{t_n}+\frac{\Delta t}{2}k_i, t_n+\frac{\Delta t}{2}) \quad i=1,2 \\ &k_4 = f(h_{t_n}+\Delta tk_3, t_n+\Delta t)\\ \end{aligned} \tag{5.4}
htn+1=htn+6k1+2k2+2k3+k4Δtk1=f(htn,tn)ki+1=f(htn+2Δtki,tn+2Δt)i=1,2k4=f(htn+Δtk3,tn+Δt)(5.4)
神经微分方程则是去利用神经网络去拟合
f
(
h
t
,
t
)
f(h_t,t)
f(ht,t),通过数值解求得当前拟合函数的结果,与真实采样数据做损失函数,不断优化,直到神经网络拟合的
f
(
h
t
,
t
)
f(h_t,t)
f(ht,t)足够好。
备注:在数据集中的视频文件是一位南朝鲜的老师关于Neural ODE的授课音频(英语),想学习Neural ODE的同学不妨下载下来看看。
6. 模型介绍
模型的主体结构是VAE的Encoder-Decoder结构,编码器和解码器都是由RNN构成的,二者中间有一个神经微分方程节点用于处理Encoder提取到的关键信息,具体原理图和结构图可见下图


6.1 Encoder and Decoder
编码器和解码器的结构简单,以循环神经网络为主体,结构代码见下
# 编码器
class Encoder(nn.Layer):
""" Encoder : transforms the input from data to latent
space using a Seq2Vec architecture """
def __init__(self, latent_dim, obs_dim, hidden_units, hidden_layers):
super(Encoder, self).__init__()
self.rnn = nn.GRU(obs_dim, hidden_units, hidden_layers, time_major=False)
self.h2o = nn.Linear(hidden_units, latent_dim * 2)
def forward(self, x):
y, _ = self.rnn(x)
# take last step trough the dense layer
y = y[:, -1, :]
y = self.h2o(y)
return y
# 解码器
class Decoder(nn.Layer):
""" Decoder : transforms the input from latent to data space using a
Seq2Seq architecture """
def __init__(self, latent_dim, obs_dim, hidden_units, hidden_layers):
super(Decoder, self).__init__()
self.act = nn.Tanh()
self.rnn = nn.GRU(latent_dim, hidden_units, hidden_layers, time_major=False)
self.h1 = nn.Linear(hidden_units, hidden_units - 5)
self.h2 = nn.Linear(hidden_units - 5, obs_dim)
def forward(self, x):
y, _ = self.rnn(x)
y = self.h1(y)
y = self.act(y)
y = self.h2(y)
return y
6.2 神经微分方程模块
神经微分方程模块参考了torchdiffeq模块,具体实现参考SimpleODEInt.py,今后考虑丰富这部分内容,感兴趣的可以留言一起学习。本次用来拟合
f
(
h
t
,
t
)
f(h_t,t)
f(ht,t)的函数是使用线性函数和激活函数配合搭建的,具体代码见下
class LatentOdeF(nn.Layer):
""" ODE-NN: takes the value z at the current time step and outputs the
gradient dz/dt """
def __init__(self, layers):
super(LatentOdeF, self).__init__()
self.act = nn.Tanh()
self.layers = layers
# Feedforward architecture
arch = []
for ind_layer in range(len(self.layers) - 2):
layer = nn.Linear(self.layers[ind_layer],
self.layers[ind_layer + 1],
weight_attr= paddle.framework.ParamAttr(initializer=nn.initializer.XavierUniform()))
arch.append(layer)
layer = nn.Linear(self.layers[-2],
self.layers[-1],
weight_attr=nn.initializer.Constant(value=0.0))
arch.append(layer)
self.linear_layers = nn.LayerList(arch)
self.nfe = 0
def forward(self, t, x):
self.nfe += 1
for ind in range(len(self.layers) - 2):
x = self.act(self.linear_layers[ind](x))
# last layer has identity activation (i.e linear)
y = self.linear_layers[-1](x)
return y
7. 文件结构
├── cylinderData.pkl # 数据集
├── VKS_node.py # Neural ODE模型
├── VKS_lstm.py # 对比的LSTM模型
├── result.py # 输出结果绘制、处理
├── SimpleODEInt.py # 仿照torchdiffeq写的paddlepaddle处理常微分方程的文件
8. 结果展示
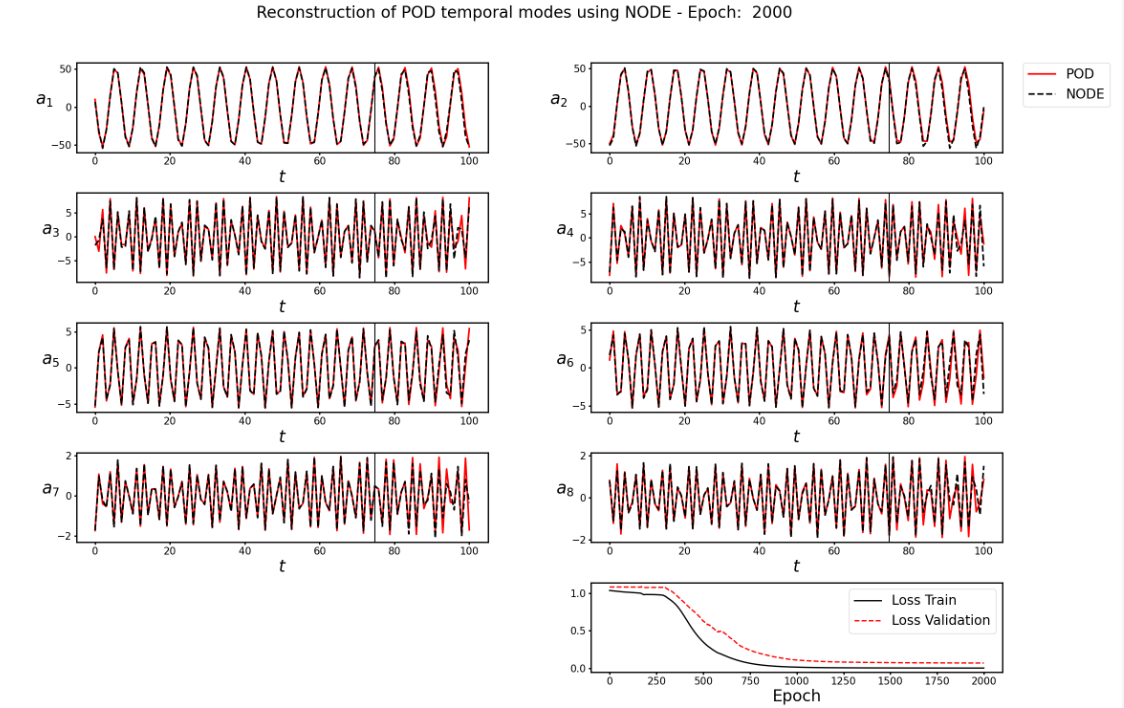
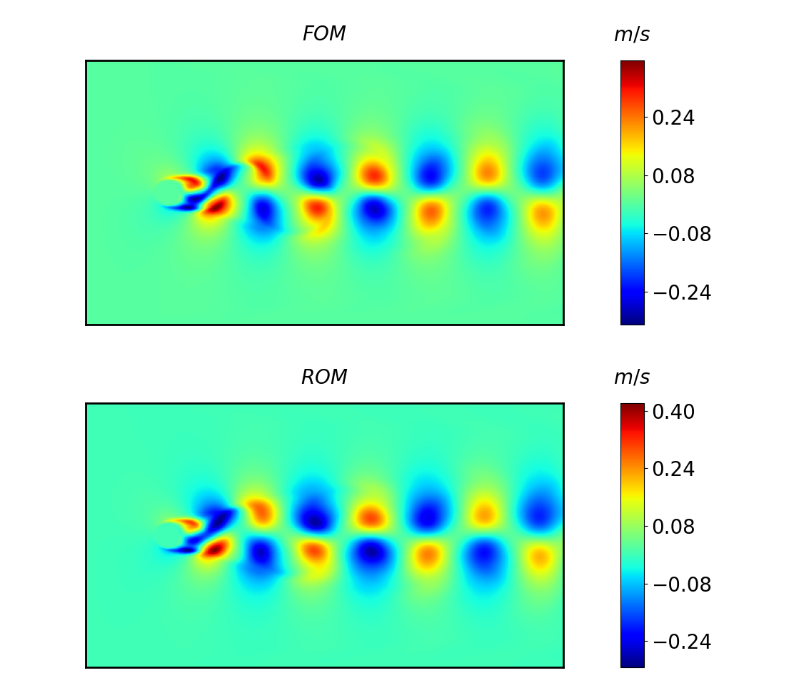
结果展示分为两部分,一部分是将Decoder还原的时间参数与原时间参数对比,查看拟合结果;另一部分是利用还原的时间参数重构时空系统,查看重构效果。时间参数拟合图中8.1(a)代表
t
∈
[
0
,
100
]
t \in [0,100]
t∈[0,100]时VAE的拟合结果;图8.1(b)代表作为对比的LSTM模型的时间参数拟合结果图;图8.1©(d)分别代表
t
∈
[
100
,
200
]
t \in [100,200]
t∈[100,200]和
t
∈
[
20
,
300
]
t \in [20,300]
t∈[20,300]时的VAE、LSTM重构效果对比图;
t
=
250
t=250
t=250和
t
=
300
t=300
t=300时的重构效果图见图8.2;流体绕过圆柱后的速度预测见图8.3
8.1. 代码运行2000次,对8个时间参数的拟合结果见下图


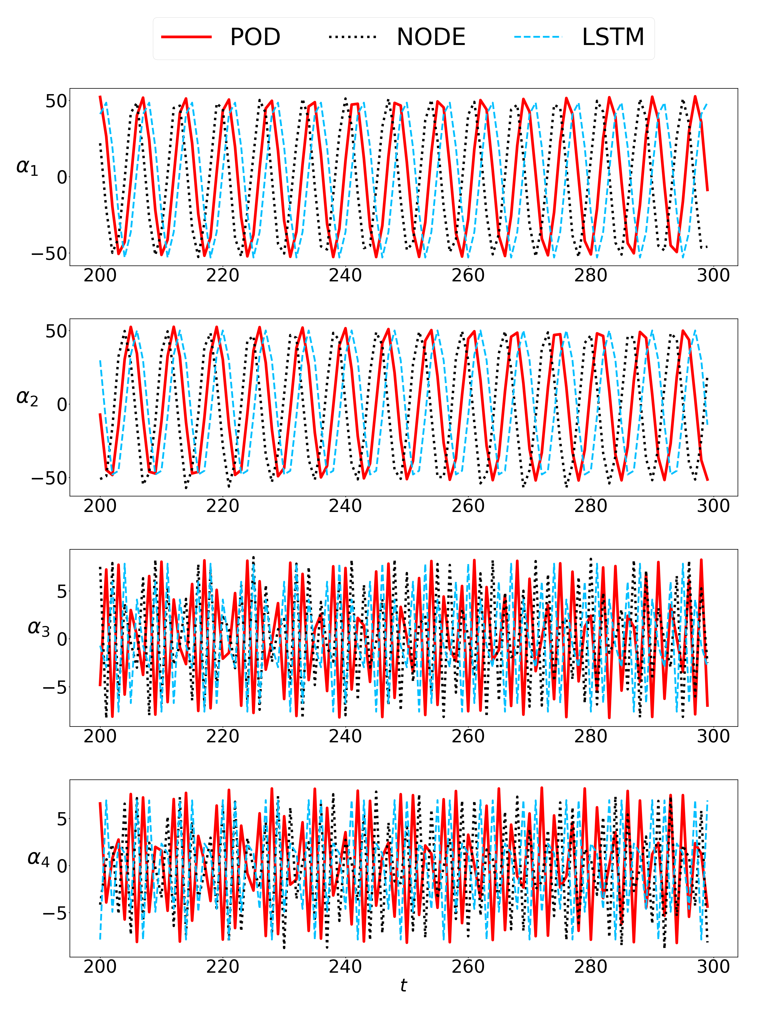
8.2. 重构时空系统的结果见下图

9. 结果说明
作为一个时序预测模型,论文中使用了25%的数据(前75个)进行训练,用第76到100的25个数据做验证,用后200条数据做预测,由于所用的时序数据比较少,因此在
t
=
200
t=200
t=200时预测结果与真实结果会有一定差异,这在正常的时序模型预测中属于正常现象,模型跑出的预测结果的效果图没有论文中的预测结果的效果图好,例如图8.1©(d)和图8.3。为此,我跑了作者提供的torch版本的源代码,其预测结果与复现模型预测结果几乎一致,后续我有进行了模型的对齐,PaddlePaddle版本与torch版本的模型前向和反向都是完全一致的,由此可见,复现的模型以及PaddlePaddle框架并没有问题,后续联系作者询问相关原因,作者没有给予明确回复。
经过加大训练的数据量,可以得到与原论文中相近的结果,图8.2就是使用90%作为训练数据所获得的重构结果,可见使用较多数据训练其结果会更好,由于复现代码与作者提供的代码对齐且运行结果一致,从复现角度来看是没有问题的。
还有一个现象是当设置随机数种子的时候,分别运行2000个iters,所得的结果会有一定差异。
9.1 模型对齐方法详解
本部分详细说明如何对齐模型,说明结果与源代码是完全一致的。本项目中整个模型分为三部分:编码器、神经微分方程Node结点和解码器,分别在torch代码中模型初始化后使用torch.save()分别保存三部分模型的权重,分别记为init_encoder.pth,init_node.pth和init_decoder.pth,这三个模型主要是使用nn.GRU()和nn.Linear()组网的,而对于torch和paddlepaddle,GRU权重矩阵维度是对应的,线性层的权重矩阵是转置关系,因此当转化模型权重(从torch到paddlepaddle)需要对应的调整。三部分转化权重的代码附在下面,保存结果分别记为: init_encoder.pdparams,init_node.pdparams和init_decoder.pdparams,相应关键代码段附在下面。
检查模型是否对齐,可以使torch版本模型和paddlepaddle版本模型同时加载上述保存好的和转化来的模型,检验两个模型输出结果是否一致,为了方便,通过打印两个模型输出的损失函数来进行验证,损失函数对比图见图9.1,通过损失函数对比可知两个模型的损失函数在框架计算误差范围内是一致的,因此可以认为模型是对齐的。

9.2 关键代码段
本部分是关于权重转化和模型加载的关键代码段,分为torch模型初始权重保存,paddle模型初始权重加载和模型各部分的权重转化。
# torch 版本模型初始化后的初始权重保存代码见下
# objects for VAE
enc = Encoder(latent_dim, obs_dim, units_enc, layers_enc).to(device)
torch.save(enc.state_dict(), 'init_encoder.pth')
node = LatentOdeF(layers_node).to(device)
torch.save(node.state_dict(), 'init_node.pth')
dec = Decoder(latent_dim, obs_dim, units_dec, layers_dec).to(device)
torch.save(dec.state_dict(), 'init_decoder.pth')
# paddle 版本模型初始化后加载转化后的初始权重的代码见下
enc = Encoder(latent_dim, obs_dim, units_enc, layers_enc)
enc_state_dict = paddle.load('init_encoder.pdparams')
enc.set_state_dict(enc_state_dict)
print('encoder has initialized \n')
node = LatentOdeF(layers_node)
node_state_dict = paddle.load('init_node.pdparams')
node.set_state_dict(node_state_dict)
print('node has initialized \n')
dec = Decoder(latent_dim, obs_dim, units_dec, layers_dec)
dec_state_dict = paddle.load('init_decoder.pdparams')
dec.set_state_dict(dec_state_dict)
print('decoder has initialized \n')
# 模型转化:pth->pdparams
# Encoder
import torch
import numpy as np
import paddle
model_dict = torch.load('init_encoder.pth')
paddle_dict = {}
for key, value in model_dict.items():
if "running_mean" in key:
key = key.replace("running_mean", "_mean")
elif "running_var" in key:
key = key.replace("running_var", "_variance")
if len(value.shape) == 2:
if 'h2o' not in key:
paddle_dict[key] = value.detach().cpu().numpy()
else:
paddle_dict[key] = np.transpose(value.detach().cpu().numpy(), [1, 0])
elif len(value.shape) == 0:
print('jump',value, key)
continue
else:
paddle_dict[key] = value.detach().cpu().numpy()
# print(key, value.shape)
print(len(paddle_dict.keys()))
paddle.save(paddle_dict, "init_encoder.pdparams")
# Node
import torch
import numpy as np
import paddle
model_dict = torch.load('init_node.pth')
paddle_dict = {}
for key, value in model_dict.items():
if "running_mean" in key:
key = key.replace("running_mean", "_mean")
elif "running_var" in key:
key = key.replace("running_var", "_variance")
if len(value.shape) == 2:
paddle_dict[key] = np.transpose(value.detach().cpu().numpy(), [1, 0])
elif len(value.shape) == 0:
print('jump',value, key)
continue
else:
paddle_dict[key] = value.detach().cpu().numpy()
# print(key, value.shape)
print(len(paddle_dict.keys()))
paddle.save(paddle_dict, "init_node.pdparams")
# Decoder
import torch
import numpy as np
import paddle
model_dict = torch.load('init_decoder.pth')
paddle_dict = {}
for key, value in model_dict.items():
if "running_mean" in key:
key = key.replace("running_mean", "_mean")
elif "running_var" in key:
key = key.replace("running_var", "_variance")
if len(value.shape) == 2:
if 'h2' not in key and 'h1' not in key:
paddle_dict[key] = value.detach().cpu().numpy()
else:
paddle_dict[key] = np.transpose(value.detach().cpu().numpy(), [1, 0])
elif len(value.shape) == 0:
print('jump',value, key)
continue
else:
paddle_dict[key] = value.detach().cpu().numpy()
# print(key, value.shape)
print(len(paddle_dict.keys()))
paddle.save(paddle_dict, "init_decoder.pdparams")
10. 配置需求
| 环境需求 | 显卡需求 |
|---|---|
| paddlepaddle=2.2.2 | RTX3070 x 1 |
11. 快速开始
# 数据集准备
%cd VAE_Neural_ODE
!mv ../data/data197821/cylinderData.pkl .
/home/aistudio/VAE_Neural_ODE
# 训练带有Neural ODE节点的VAE模型
!python VKS_node.py
# 训练对比LSTM模型
!python VKS_lstm.py
# 生成相应结果图
!python results.py
12.致谢
感谢百度相关负责人周哥认真讨论解决相关问题,让这个项目更加完善;感谢我的师兄AI4Science负责人博哥的指导;特别感谢新飞姐(网名:芋泥啵啵/飞桨腹黑花花)提供的一系列的帮助(包括但不限于提供算力、帮忙干杂活等)。
此文章为搬运
原项目链接























 2290
2290

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








