目录
一、组合总和
力扣第39题
本题采用回溯的思想解决
1.1 具体思路
首先定义一个递归函数 backtrack,该函数接受当前的组合列表 combination 和当前位置索引 start。
在回溯函数中,首先判断当前目标值是否等于 0。如果等于 0,则将当前组合添加到结果列表中,并返回。
如果目标值小于 0,或者已经遍历到数组的末尾,直接返回。
对于每个候选数,从当前位置索引开始,依次进行如下操作:
·将当前候选数添加到组合列表中。
·调用回溯函数 backtrack,传入新的目标值(target - 候选数)和更新后的位置索引(start)。
·回溯完成后,将最后添加的候选数从组合列表中移除。
在主函数中,初始化结果列表和组合列表,调用回溯函数 backtrack。
1.2 思路展示
假设我们有候选数组 [2, 3, 6, 7] 和目标数 7。我们可以通过画出一个树状图来展示回溯的过程。
首先是整体结构:
[]
/ | \
2 3 6 7
接下来我们开始从根节点 [] 开始遍历:
选择 2:
[2]
/ | \
2 3 6 7
选择 2:
[2, 2]
/ | \
2 3 6 7
选择 2:
[2, 2, 2]
/ | \
2 3 6 7
此时,目标值为 1,小于 0,因此返回。
回退到上一步,选择 3:
[2, 3]
/ | \
2 3 6 7
此时,目标值为 1,小于 0,因此返回。
回退到上一步,选择 6:
[2, 6]
/ | \
2 3 6 7
此时,目标值为 1,小于 0,因此返回。
回退到上一步,选择 7:
[2, 7]
/ | \
2 3 6 7
此时,目标值为 0,将当前组合 [2, 7] 加入结果列表。
回退到 [],选择 3:
[3]
/ | \
2 3 6 7
选择 2:
[3, 2]
/ | \
2 3 6 7
选择 2:
[3, 2, 2]
/ | \
2 3 6 7
此时,目标值为 2,继续向下选择。...
以上就是回溯的过程,通过逐步选择候选数并进行回溯,不断尝试各种组合,直到得到所有满足条件的组合。
1.3 代码实现
def combinationSum(candidates, target):
res = [] # 存储结果的列表
def backtrack(combination, start, target):
if target == 0: # 目标值为0,将当前组合添加到结果列表
res.append(combination)
return
if target < 0 or start == len(candidates): # 目标值小于0或已遍历到末尾,直接返回
return
for i in range(start, len(candidates)):
backtrack(combination + [candidates[i]], i, target - candidates[i])
backtrack([], 0, target) # 调用回溯函数,初始组合为空列表,起始位置为0
return res
# 示例输入
# 示例1
candidates1 = [2, 3, 6, 7]
target1 = 7
print(combinationSum(candidates1, target1)) # [[2, 2, 3], [7]]
# 示例2
candidates2 = [2, 3, 5]
target2 = 8
print(combinationSum(candidates2, target2)) # [[2, 2, 2, 2], [2, 3, 3], [5, 3]]
# 示例3
candidates3 = [2]
target3 = 1
print(combinationSum(candidates3, target3)) # []1.4 复杂度分析
(1)时间复杂度:
回溯函数的时间复杂度取决于结果的数量。假设结果数量为R,每个结果平均长度为L,那么回溯函数的时间复杂度为O(R * L)。
在最坏情况下,假设候选列表长度为N,目标值为T,结果数量为R,结果平均长度为L,则回溯函数的时间复杂度为O(N^T * R * L)。
(2)空间复杂度:
回溯函数使用了递归调用,同时维护了一个存储结果的列表。在最坏情况下,结果数量为R,结果平均长度为L,空间复杂度为O(R * L)。
同时,递归调用的深度为目标值T,所以空间复杂度为O(T)。
但需要注意的是,以上复杂度分析都是基于没有剪枝等优化措施的实现。
1.5 运行结果

二、全排列
力扣第47题

本题采用回溯的思路解决
2.1 具体思路
首先对输入的nums数组进行排序,这样相同的数字会相邻排列。
创建一个布尔数组used,用于标记nums中的元素是否被使用过,初始化为False。
创建一个空列表res,用于存储最终的全排列结果。
定义一个回溯函数backtrack,该函数采用一个当前排列combination作为参数。
在backtrack函数中,如果combination的长度等于nums的长度,将其加入到结果res中,并返回。
否则,遍历nums数组,对于每个元素,如果它已经被使用(used[i]为True)或者与前一个元素相同且前一个元素未被使用,则跳过。
如果当前元素未被使用,将其标记为已使用,将其加入到combination中,然后递归调用backtrack函数。
递归调用完成后,将当前元素的使用状态还原,以便尝试其他分支。
2.2 思路展示
以输入数组nums = [1, 1, 2]为例。
初始状态是一个空列表[],表示当前排列为空。
在第一层的递归中,我们遍历到了元素1,因为它是第一个不重复的数,所以我们选择使用它。将1加入到当前排列中,并将其标记为已使用。进入下一层递归。
在第二层的递归中,我们继续遍历到了元素1,但由于前一个元素1已经被使用,所以我们跳过这个分支。
在第三层的递归中,我们遍历到了元素2,它是第一个不重复的数,所以我们选择使用它。将2加入到当前排列中,并将其标记为已使用。此时,当前排列为[1, 2]。
因为当前排列的长度等于输入数组的长度,所以将当前排列[1, 2]加入到最终结果中。
回溯到上一层递归,将元素2的使用状态还原,并从当前排列中移除元素2。
在第三层的递归中,我们遍历到了元素1,但由于前一个元素2已经被使用,所以我们跳过这个分支。
回溯到上一层递归,将元素1的使用状态还原,并从当前排列中移除元素1。
在第二层的递归中,我们遍历到了元素2,因为它是第一个不重复的数,所以我们选择使用它。将2加入到当前排列中,并将其标记为已使用。此时,当前排列为[2, 1]。
因为当前排列的长度等于输入数组的长度,所以将当前排列[2, 1]加入到最终结果中。
回溯到上一层递归,将元素2的使用状态还原,并从当前排列中移除元素2。
在第二层的递归中,我们遍历到了元素1,因为它是第一个不重复的数,所以我们选择使用它。将1加入到当前排列中,并将其标记为已使用。此时,当前排列为[1, 1]。
因为当前排列的长度等于输入数组的长度,所以将当前排列[1, 1]加入到最终结果中。
回溯到上一层递归,将元素1的使用状态还原,并从当前排列中移除元素1。
最终得到的全排列结果为[[1, 2], [2, 1], [1, 1]]。
2.3 代码实现
def permuteUnique(nums):
nums.sort() # 排序输入数组
res = [] # 存储结果的列表
used = [False] * len(nums) # 标记元素是否被使用的列表
def backtrack(combination):
if len(combination) == len(nums): # 如果组合长度等于数组长度,说明找到了一个全排列
res.append(combination[:]) # 将当前组合加入结果
return
for i in range(len(nums)):
if used[i] or (i > 0 and nums[i] == nums[i-1] and not used[i-1]):
continue # 如果元素已被使用或者与前一个元素相同且前一个元素未被使用,则跳过该元素
used[i] = True # 标记当前元素为已使用
combination.append(nums[i]) # 将当前元素加入组合
backtrack(combination) # 递归调用
used[i] = False # 回溯时,将当前元素标记为未使用
combination.pop() # 回溯时,将当前元素从组合中移除
backtrack([])
return res
# 示例输入
nums1 = [1, 1, 2]
nums2 = [1, 2, 3]
# 调用函数,输出结果
print(permuteUnique(nums1))
print(permuteUnique(nums2))2.4 复杂度分析
(1)时间复杂度:该算法的时间复杂度取决于生成的全排列数量,即 O(n*n!),其中 n 是输入数组的长度。
(2)空间复杂度:该算法的空间复杂度主要取决于存储结果的列表 res 和标记数组 used,因此空间复杂度为 O(n*n!)。
2.5 运行结果
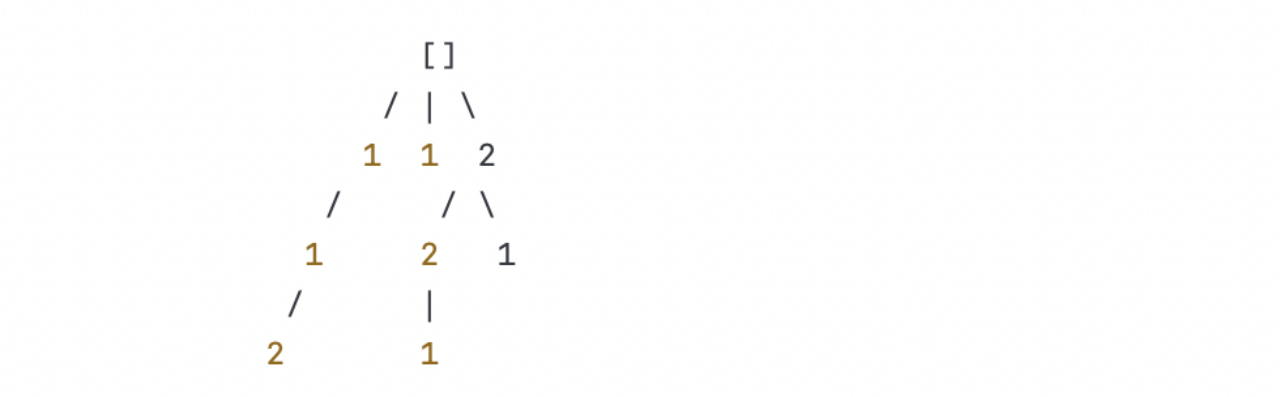
与预期结果均保持一致
三、N皇后问题
力扣第52题

本题依旧采用回溯的思想解题
3.1 具体思路
对于 n 皇后问题,我们可以使用一个数组 queens 来表示每个皇后所在的列位置。数组的索引表示行位置,该索引处的值表示该行皇后所在的列位置。
详细过程如下
首先定义一个计数器 count,用于记录符合条件的解决方案数量。
定义一个辅助函数 backtrack(row, queens) 来递归地生成解决方案。
·如果 row 等于 n,说明所有行的皇后都已放置完毕,此时将 count 加一并返回。
·否则,遍历当前行的每一列位置,依次尝试放置皇后。
如果当前位置不与之前已放置的皇后冲突(不在同一列、同一对角线上)
则将当前位置加入 queens 数组,并递归调用 backtrack(row+1, queens) 进行下一行的放置。
放置完毕后,需要将 queens 数组回溯到之前的状态,以便尝试其他的位置。
在主函数中调用 backtrack(0, []) 开始生成解决方案。
返回计数器 count,即不同的解决方案数量。
3.2 思路展示
初始状态 queens = [-1, -1, -1, -1]
0 1 2 3
---------------------
0 | Q
1 |
2 |
3 |
第一步:放置第一个皇后(在第 0 行)
尝试在第 0 行的每一列位置放置皇后,并递归进入下一行:
放置皇后在 (0, 0) 位置后,状态 queens = [0, -1, -1, -1]
0 1 2 3
---------------------
0 | Q
1 |
2 |
3 |
第二步:放置第二个皇后(在第 1 行)
尝试在第 1 行的每一列位置放置皇后,并递归进入下一行:
放置皇后在 (1, 2) 位置后,状态 queens = [0, 2, -1, -1]
0 1 2 3
---------------------
0 | Q
1 | Q
2 |
3 |
第三步:放置第三个皇后(在第 2 行)
尝试在第 2 行的每一列位置放置皇后,并递归进入下一行:
放置皇后在 (2, 1) 位置后,状态 queens = [0, 2, 1, -1]
0 1 2 3
---------------------
0 | Q
1 | Q
2 | Q
3 |
第四步:放置第四个皇后(在第 3 行)
尝试在第 3 行的每一列位置放置皇后,并递归进入下一行:
放置皇后在 (3, 3) 位置后,状态 queens = [0, 2, 1, 3]
0 1 2 3
---------------------
0 | Q
1 | Q
2 | Q
3 | Q
这个时候找到了一个解
然后程序回溯到第三步,将queens[2]=1 去掉,再寻找第四部的位置,依次类推可求出结果。
3.3 代码实现
def totalNQueens(n):
count = 0
def backtrack(row, queens):
nonlocal count
if row == n:
count += 1
return
for col in range(n):
if is_valid(row, col, queens):
queens.append(col)
backtrack(row + 1, queens)
queens.pop()
def is_valid(row, col, queens):
for i in range(row):
if col == queens[i] or row - i == abs(col - queens[i]):
return False
return True
backtrack(0, [])
return count
# 示例输入
n = 4
# 调用函数,输出结果
print(totalNQueens(n))
m = 1
# 调用函数,输出结果
print(totalNQueens(m))3.4 复杂度分析
(1)时间复杂度: 在最坏的情况下,需要遍历整个棋盘的所有位置,因此时间复杂度为 O(n^2)。回溯算法的时间复杂度通常是指数级别的,但由于该问题的特殊性,回溯过程中每行只能放置一个皇后,因此可以将时间复杂度简化为 O(n^2)。
(2)空间复杂度: 空间复杂度取决于递归调用的层数,最多不会超过 n。每次递归调用都会创建一个 queens 数组,空间复杂度为 O(n)。因此,总的空间复杂度为 O(n)。
3.5 运行结果
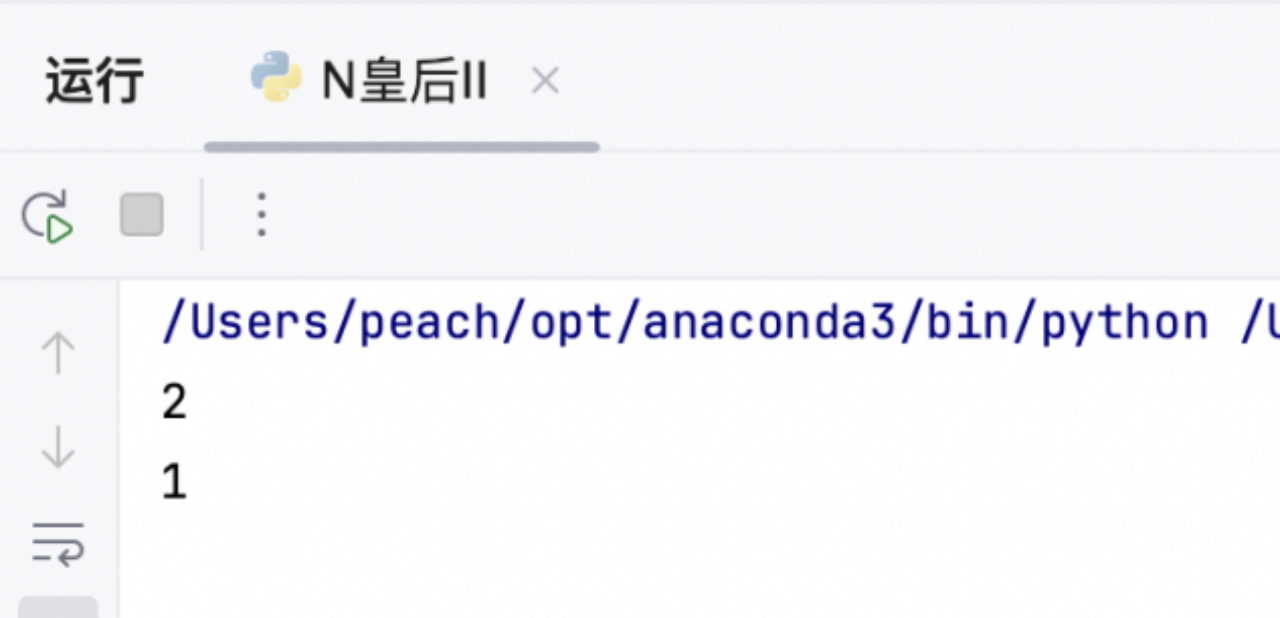
与n=4和n=2的结果保持一致
四、子集II
力扣第90题

本题采用回溯的思想
4.1 具体思路
首先对数组进行排序,这样重复元素会相邻排列。
创建一个辅助函数 backtrack,该函数接收当前位置索引 start、当前正在构建的子集 subset 和最终结果集 result 作为参数。
在 backtrack 函数中,首先将当前子集 subset 加入到结果集 result 中。
然后从 start 开始遍历数组 nums:
如果当前索引 i 大于 start,并且 nums[i] 等于 nums[i-1],则跳过该元素,避免重复。
否则,将 nums[i] 加入到子集 subset 中,并以 i+1 为起始位置递归调用 backtrack。
在递归完成后,将最后一个加入的元素从子集 subset 中移除,以便尝试其他可能性。
最后返回结果集 result。
4.2 思路展示
针对示例数组 [1,2,2] 进行回溯的过程示意图:
初始状态:subset = [], result = []
回溯到第一层:
subset = [],result = [[]]
- 加入空子集 [] 到结果集
回溯到第二层:
subset = [1],result = [[], [1]]
- 加入子集 [1] 到结果集
回溯到第三层:
subset = [1, 2],result = [[], [1], [1, 2]]
- 加入子集 [1, 2] 到结果集
回溯到第四层:
subset = [1, 2, 2],result = [[], [1], [1, 2], [1, 2, 2]]
- 加入子集 [1, 2, 2] 到结果集
回溯到第五层:
subset = [1, 2],result = [[], [1], [1, 2], [1, 2, 2]]
- 由于 nums[i] == nums[i-1],跳过该元素,避免重复
回溯到第六层:
subset = [1],result = [[], [1], [1, 2], [1, 2, 2]]
- 由于 nums[i] == nums[i-1],跳过该元素,避免重复
回溯到第七层:
subset = [],result = [[], [1], [1, 2], [1, 2, 2], [2]]
- 加入子集 [2] 到结果集
回溯到第八层:
subset = [2, 2],result = [[], [1], [1, 2], [1, 2, 2], [2], [2, 2]]
- 加入子集 [2, 2] 到结果集
回溯到第九层:
subset = [2],result = [[], [1], [1, 2], [1, 2, 2], [2], [2, 2]]
- 由于 nums[i] == nums[i-1],跳过该元素,避免重复
回溯结束
最终结果:[[], [1], [1, 2], [1, 2, 2], [2], [2, 2]]
4.3 代码实现
def subsetsWithDup(nums):
nums.sort() # 对数组排序
result = []
def backtrack(start, subset):
result.append(subset[:]) # 将当前子集加入结果集
for i in range(start, len(nums)):
if i > start and nums[i] == nums[i-1]: # 避免重复
continue
subset.append(nums[i]) # 将当前元素加入子集
backtrack(i + 1, subset) # 递归调用
subset.pop() # 回溯,将最后一个元素移除
backtrack(0, [])
return result
# 示例输入
nums1 = [1, 2, 2]
nums2 = [0]
# 调用函数,输出结果
print(subsetsWithDup(nums1)) # 输出示例1的结果
print(subsetsWithDup(nums2)) # 输出示例2的结果4.4 复杂度分析
(1)时间复杂度:在最坏情况下,由于要生成所有可能的子集,时间复杂度为O(2^n),其中n是输入数组的长度。另外由于排序操作的时间复杂度为O(nlogn),因此总体时间复杂度为O(nlogn + 2^n)。
(2)空间复杂度:递归调用会占用一定的栈空间,因此空间复杂度为O(n),其中n是输入数组的长度。此外,存储结果集的空间复杂度也为O(2^n),因为子集的个数是指数级别的。
4.5 运行结果
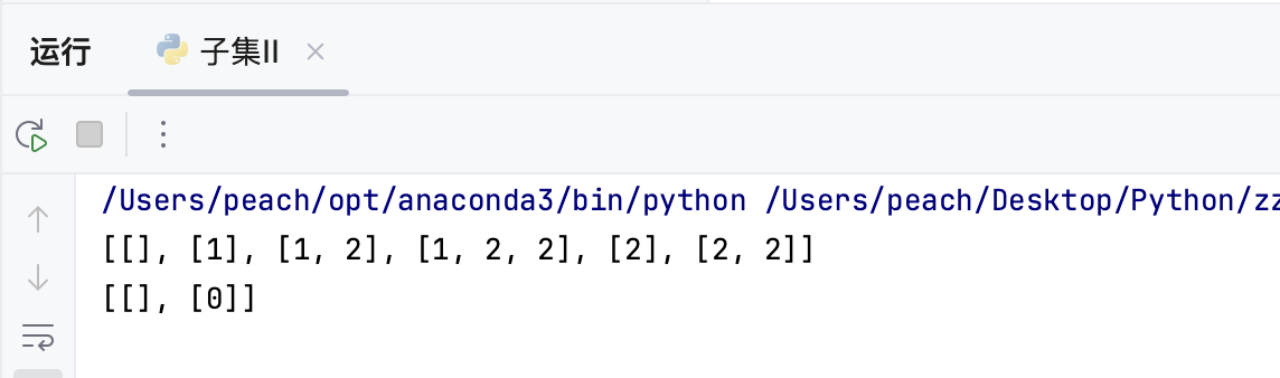
结尾语
好好学习,天天向上























 1278
1278











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










