2021年高教社杯全国大学生数学建模竞赛题目《中药材的鉴别》

E题         中药材的鉴别

        不同中药材表现的光谱特征差异较大，即使来自不同产地的同一药材，因其无机元素的化学成分、有机物等存在的差异性，在近红外、中红外光谱的照射下也会表现出不同的光谱特征,因此可以利用这些特征来鉴别中药材的种类及产地。
        中药材的种类鉴别相对比较容易,不同种类的中药材呈现的光谱的区别比较明显。图1为两种不同药材的近红外光谱数据曲线图，容易看出两者的差异比较大。
        中药材的道地性以产地为主要指标,产地的鉴别对于药材品质鉴别尤为重要。然而，不同产地的同一种药材在同一波段内的光谱比较接近，使得光谱鉴别的误差较大。另外，有些中药材的近红外区别比较明显，而有些药材的中红外区别比较明显(见图2和图3所给出的来自某药材5个不同产地的近红外和中红外光谱数据曲线图)。当样本量不够充足时，我们可以通过近红外和中红外的光谱数据相互验证来对中药材产地进行综合鉴别。
        附件1至附件4是一些中药材的近红外或中红外光谱数据，其中No列为药材的编号，Class列表示中药材的类别，OP列表示该种药材的产地，其余各列第一行的数据为光谱的波数(单位cm')、第二行以后的数据表示该行编号的药材在对应波段光谱照射下的吸光度（注:该吸光度为仪器矫正后的值，可能存在负值〉。试建立数学模型，研究解决以下问题。
        问题1.根据附件1中几种药材的中红外光谱数据，研究不同种类药材的特征和差异性，并鉴别药材的种类。
        问题⒉.根据附件2中某一种药材的中红外光谱数据，分析不同产地药材的特征和差异性，试鉴别药材的产地，并将下表中所给出编号的药材产地的鉴别结果填入表格中。

        问题3.根据附件3中某一种药材的近红外和中红外数据，试鉴别该种药材的产地，并将下表中所给出编号的药材产地的鉴别结果填入表中。 

        问题4.附件4给出了几种药材的近红外光谱数据，试鉴别药材的类别与产地，并将下表中所给出编号的药材类别与产地的鉴别结果填入表各中。         

说明1.道地药材的信息可参阅百度百科(https://baike.baidu.com/item/道地药材/1950482?fr=aladdin)。
说明2．红外光谱分析的信息可参阅百度百科(https://baike.baidu.com/item/红外光谱分析)。 

中药材的鉴别与优化分类

摘要

        根据不同中药材在近红外、中红外光谱的照射下表现的光谱特征具有较大差异，本文主要根据光谱特征进行鉴别中药材的种类及其产地。建立了数据可视化分布模型，利用了改进的K-means聚类模型、相关系数、距离判别法、平均相关系数和BP神经网络等模型。

        对于问题一:首先，将附件 1 的光谱数据可视化，直观的分析了不同药材的分布特征和差异；其次，利用Python的Matplotlib库将附件1的数据绘制成直方图(见附录1)，确定了大致可分为3类；最后，建立了K-means聚类模型，第三类数据直观上差异较大，故又建立了改进的K-means聚类模型，不先指定类数，再次验证了分为3类是合理的。

        对于问题二:首先，利用Matplotlib库将同一产地不同波数下的数据求均值，并可视化，分析了不同产地的特征及差异；其次，利用Python数据分析未知产地数据，与已知产地的数据进行计算相关性系数Ai，产地J的相关系数求平均，即。最大，说明属于产地J,最后，建立了反向传播神经网络模型进行了第二次分产地演算，得到了产地的归属。

        对于问题三:首先，利用Python的corr函数求得了未知产地和已知产地的相关系数，将同一产地的相关系数求平均，分别得到了中红外、近红外下，未知产地和各已知产地的平均相关系数；其次，利用同一未知产地的中红外、近红外平均相关系数差异较大的，确定了产地归属；最后，将中红外、近红外合并到一起，建立了BP神经网络模型，通过训练，测试，得到了各产地归属。

对于问题四:首先，分析数据得出，药材种类或产地缺一的数据并非所求，因此，种类或产地缺失的数据剔除；其次，把A、B、C三类含药材各产地的数据导入python，并求出要求数据与各类各产地的平均相关系数(附录5)；最后，通过比较平均相关系数，同时得到了未知数据的种类和产地。

关键词：改进的K-means聚类模型，相关系数，平均相关系数，BP神经网络，距离判别法

一、问题重述

1.1问题背景

        随着中药材种类数据量的增加，对中药材鉴别技术已经普遍使用同时越来越收到重视。有利于相关人员进行管理和后期的维护。中药材的道地性以产地为主要指标，产地的鉴别对于药材品质鉴别也尤为重要。

1.2问题提出

        根据以上背景，以及给出的四个附件，需要解决以下问题：

        问题1.我们以附件1测量的数据为参考标准，用Python将其数据图绘制如图1所示。根据附件 1 中几种药材的中红外光谱数据，来研究不同种类药材的特征和差异性，并且鉴别药材的种类等。

        问题2.分析未知产地数据，每一组未知产地数据都与已知中药材产地的数据进行计算中红外相关性系数，而同一组中药材产地又有多种不同的中药材编号，即表明该产地有很多不同种类的中药材，需计算出中红外平均相关系数。再将未知产地与各个已知产地的中红外平均相关系数进行对比得出中药材产地的关系。根据附件 2中某一种药材的中红外光谱数据，分析不同产地药材的特征和差异性，试鉴别药材的产地。方法（2）.BP网络具有强泛化性能，使网络平滑地学习，使网络合理地相应被训练以外的输入，用MATLAB程序逼近神经网络模型函数，提高精度，但同时也使网络复杂化，从而增加了网络权值的训练时间。

        问题3.很容易看出原理与问题二一致，通过附件3可以发现有中红外光谱数据表和近红外光谱数据表，利用Python分析出对应的近红外和中红外平均相关系数，而我们就是要选出一个更容易区分中药材产地的光谱表，再去鉴别该种药材的产地。

        问题4.通过对附件4数据的分析，可以看出三类：知道已知产地和药材类型、不知道已知产地但知道药材类型，知道已知产地但不知道药材类型，就对这三类数据和（产地和药材类型为空值）的数据进行相关系数的计算得出平均相关系数然后做出判断分析出（产地和药材类型为空值）的数据结果。再鉴别药材的类别与产地。

二、问题分析

2.1问题一的分析

        题目要求分析几种药材的中红外光谱数据，研究不同种类药材的特征和差异性，并鉴别药材的种类。我们把附件1的数据导入Python,使用Python统计出不同种类药材的折线统计图，我们就可以直观的看出光谱的波数和吸光度的趋势，和不同中药材数据的走向，以波数和吸光度来研究药材的不同种类，以及特征和差异性。

2.2问题二的分析

        题目要求根据附件2中某一种药材的中红外光谱数据，分析不同产地药材的特征和差异性，并鉴别药材的产。中红外平均相关系数。通过Python来计算未知产地的和已知产地的平均相关系数，来进行对比两者的相似程度，越接近1的就说明空白产地与已知产地的相似程度越高。（2）BP网络是由一个输入层、一个输出层和隐含层为模型结构组成的神经网络。BP网络如果超出训练范围值的输入必将产生大的输出误差，输入和输出之间的非线性关系不能用一个线性网络精确地设计出，但线性网络可以产生一个具有误差平方和最小的线性逼近。

2.3问题三的分析

第三问的原理与问题二一致，需要将两个表格合并，然后分析中红外和近红外光谱数据结果即可。首先分别分析中红外平均相关系数F1和近红外相关系数F2，看两者谁更容易区分中药材的产地，再去利用中红外光谱数据或者近红外光谱数据去研究中药材的产地。理论过程与问题二同理，计算未知产地的和已知产地的平均相关系数，越接近1的就说明空白产地与已知产地的相似程度越高。

2.4问题四的分析

假设只用已知种类或产地之一的数据进行计算可能误差会很大，所以用种类产地都已知的数据进行计算，查看种类产地都未知的数据和种类产地都已知的数据的平均相关系数，如果基本的平均相关系数都接近1，那么就说明用种类产地都已知的数据和种类产地都未知的数据进行比较误差小，所以就采用种类产地都已知的数据和种类产地都未知的数据进行平均相关系数的计算来确定种类产地都未知的数据的产地和药材类型。

三、模型假设

1.假设题目所给的所有数据真实可靠；

2.假设收集近红外光谱数据稳定性，可以准确记录数据；

3.在利用Python、Excel计算时，假设计算的有效数字取舍误差可以忽略不计；

4.假设中药材在检测数据时没有损坏的；

5.假设对中药材数据采集时没有人为因素；

6.假设附件4中种类产地缺一的药材的缺失信息，在已知信息的范围中。

四、符号说明

         

      

五、模型建立与求解

5.1 问题一

   针对本问题，附件 1 中提供几种药材的中红外光谱数据，使用K-means(K

均值算法)将药材编号No经行聚类划分。在聚类完成以后可以通过对类内数据的统计性分析，得到不同种类药材的特征和差异性。具体可以通过一些统计函数来实现。中红外光谱数据模型图如5-1所示。

K均值聚类算法的目标函数为：

（1）    

为了求极值，我们令损失函数求偏导数且等于0；     

           （2）

k是指第K个中心点，于是有：

根据K-means算法模型，再结合Python将附件1的几种药材的中红外光谱数据，绘制了图5-1中红外光谱数据模型图，可以直观的研究不同种类药材的特征和差异性，并鉴别药材的种类。

                                        图 5-1中红外光谱数据模型图

如图所示：

1.特点：从图中可以看出图形的趋势有3类，所以把药材的种类归纳为3种。

2.差异：不同种类药材在同一波数（cm-1）下所对应的吸光度不同

5.2 问题二

        针对本问题，为了分析已有数据和模型的误差，首先我们根据附件2的中红外光谱数据，从表中观察到一共有11种产地，用Python把中红外光谱数据中属于同一产地的归纳在一起，用皮尔森相关系数rxy，建立数学模型。

    (4)

        Spearman秩相关系数通常被认为是排列后的变量之间的Pearson线性相关系数,在实际计算中，有更简单的计算ρs的方法。假设原始的数据xi，yi已经按从大到小的顺序排列，记x'i,y'i为原xi,yi在排列后数据所在的位置，则x'i,y'i称为变量x'i, yi的秩次，则di=x'i-y'i为xi，yi的秩次之差。

如果没有相同的秩次，则ρs可由下式计算：

   (5) 

                    

如果有相同的秩次存在，那么就需要计算秩次之间的Pearson的线性相关系数：

                  (6)                         

注释：不满足连续数据，正态分布，线性关系，用spearman相关系数是最恰,当两个定序测量数据之间也用spearman相关系数。

利用Python计算出附件2中红外光谱的已知产地与未知产地平均相关系数，借助EXCEL统计出了已知产地与未知产地的平均相关系数，其图示如图5-2所示。

                                        图5-2 已知产地与未知产地的平均相关系数图

	No3	No14	No38	No48	No58	No71	No79	No86
最大平均相关系数	0.99371	0.98300	0.99437	0.98535	0.97950	0.99118	0.99502	0.99255

	No89	No110	No134	No152	No227	No331	No618
最大平均相关系数	0.99214	0.99218	0.99651	0.99304	0.99404	0.98859	0.99277

表 5-1 已知产地与未知产地最大的平均相关系数表

注释：精确到小数点后5位数

见附录3，通过对已知产地与未知产地最大的平均相关系数可分析得出未知产地的所属产地如表5-2所示。

表5-2 药材产地的鉴别结果表

No	3	14	38	48	58	71	79	86	89	110	134	152	227	331	618
OP	3	1	9	1	8	5	9	9	3	5	9	9	9	4	3

分析不同产地药材的特征和差异性：

     见附录4，用Python将各个产地再不同波数下的平均吸光度计算出来，放

入Excel中如图5-3所示。

                                                        图 5-3 不同产地平均吸光度图

如图所示：

1.特点：随着中药材产地编号的递增，药材的普遍平均吸光度越大。

2.差异：某一种药材在中红外光的各个产地的平均吸光度关系为OP11>OP10>OP9>...>OP1。

方法二：

对于问题二，用BP网络对该问题再一次经行了演算。BP网络是由输入层

输出层和隐含层为模型结构组成的神经网络如图5-4说所示。

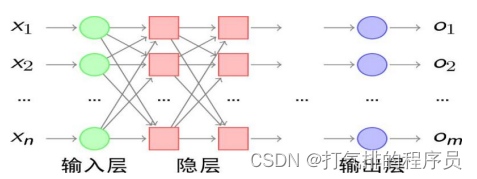
                                        图 5-4 网络模型结构图

BP算法是一种有监督式的学习算法，主要思想为，对于q个输入学习样本P1，P2，...，Pq，和对应的输出样本T1，T2，...，Tq，使网络输出层的误差平方和达到最小；利用网络的实际输出A1,A2,...，Aq，与目标矢量T1,T2,...,Tq,之间的误差修改网络权值，使Am与期望的Tm（m=l,...,q）尽可能接近。

设输入为P=(P1,P2,...,Pq),输入神经元有r个，隐含层内有s1个神经元，传递函数为F1，输出层内有s2个神经元，对应的传递函数为F2，输出为A=(A1,A2,...,Aq),目标矢量为T(T1,T2,...,Tq)。W1为输入层到隐含层的权值矩阵，B1为隐含层神经元的偏差值向量；W2为隐含层到输出层的权值矩阵，B2为输出层神经元的偏差值向量，信息的正向传递与误差的反向传播调整权值的机理如下。

信息传递

隐含层神经元的输入I1:

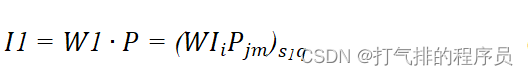
       (7)

隐含层神经元的输出A1:

      (8)

   

隐含层中第i个神经元的第m个输出a1im:

   (9)

输出层神经元的输入I2:

     (10)

输出层神经元的输出A2：

     (11)

   

输出层第k个神经元的第m个输出a2km：

  (12)

输出层第k个神经元的第m个输出a2km：

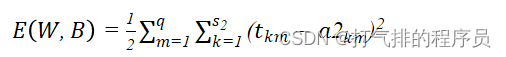          (13)

为了加快训练速度和避免陷入局部极小值，可以采用附加动量法得到改善。

1.附加动量法:
    利用附加动量的作用有可能滑过局部极小值。修正网络权值时，不仅考虑误差在梯度上的作用，而且考虑在误差曲面上变化趋势的影响，其作用如同一个低通滤波器，它允许网络忽略网络上微小变化特征。该方法是在反向传播法的基础上在每一个权值的变化上加上上一项正比于前次权值变化的值，并根据反向传播法来产生新的权值变化。
    带有附加动量因子的权值调节公式如下：
            

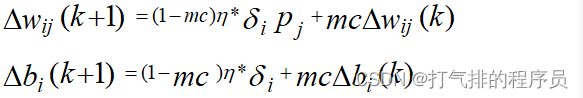
其中k为训练次数，mc为动量因子，一般取0.95左右。
    附加动量法的实质是将最后一次权值变化的影响，通过一个动量因子来传递。当动量因子取值为零时，权值变化仅根据梯度下降法产生；当动量因子取值为1时，新的权值变化则是设置为最后一次权值变化，而依梯度法 产生的变化部分则被忽略掉了；促使权值的调节向着误差曲面底部的平均变化，当网络权值进入误差曲面底部的平坦区时，δi将变得很小，于是，

，从而防止了s▲Wij=0的出现，有助于使网络从误差曲面的局部极小值中跳出。

2.自适应学习速率
    通常调节学习速率的准则是，检查权值的修正值是否真正降低了误差函数，如果确实如此，则说明所选取的学习速率值小了，可以对其增加一个量；否则可认为产生过度调节，应该减小学习速率的值。
    一种自适应学习速率的调整公式如下：
       

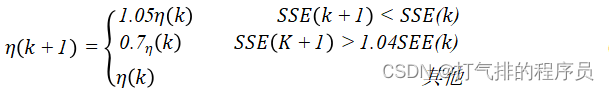
    (14)
MATLAB工具箱中带有自适应学习速率进行方向传播训练的函数为trainbpa。

        初始网络和最终网络的输出曲线见图5-5，训练过程的中间状态网络曲线见图5-6.

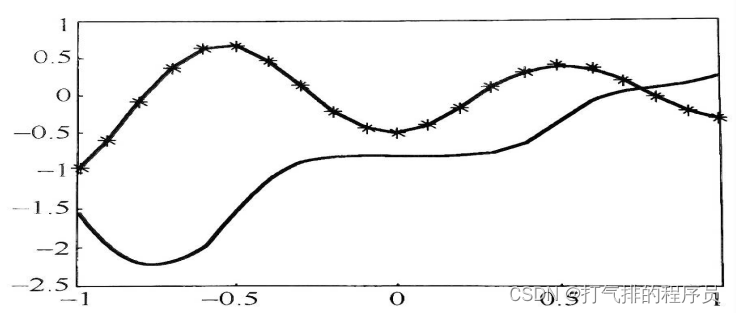
                                                图 5-5初始网络和最终网络的输出曲线

                                                        图5-6 中间训练网络的输出曲线

综上所述：通过BP神经网络模型训练出来的结果如表5-3所示

表5-3 药材产地的鉴别结果表

No	3	14	38	48	58	71	79	86	89	110	134	152	227	331	618
OP	6	1	4	6	10	6	4	11	3	4	9	6	5	7	3

5.3 问题三

针对问题三，原理与问题二一致，分析已有数据和模型，首先我们根据附件3的中红外光谱数据和近红外光谱数据分别做分析，从附件3中观察到一共有16种产地，用Python把中红外光谱数据中属于同一产地的归纳在一起，近红外光谱数据中属于同一产地的又归纳在一起，同理，用皮尔森相关系数rxy1，建立数学模型。

   (15)

同理利用Python计算出附件3中红外光谱的已知产地与未知产地平均相关系数和近红外光谱的已知产地与未知产地平均相关系数，借助EXCEL分别统计出了中红外光谱的已知产地与未知产地的平均相关系数和近红外光谱的已知产地与未知产地平均相关系数，其图示如图5-7和图5-8所示。

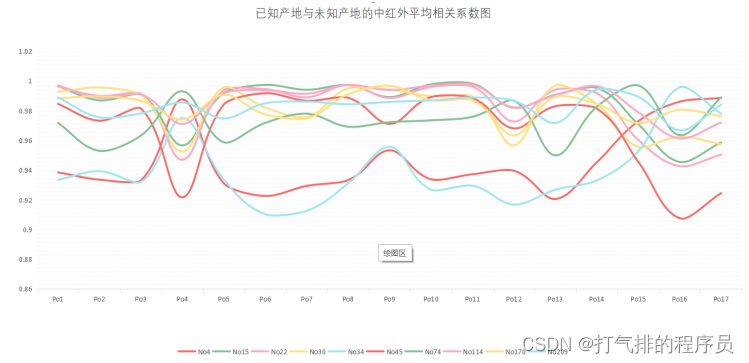
图5-7 已知产地与未知产地的中红外平均相关系数图

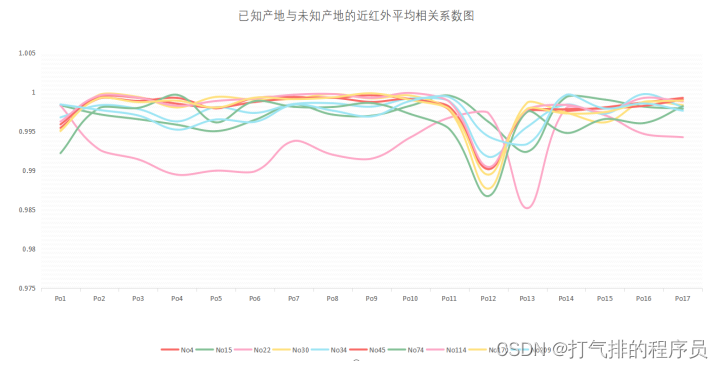
图 5-8 已知产地与未知产地的近红外平均相关系数图

图 5-9 同一组未知数据在不同红外光的平均相关系数图

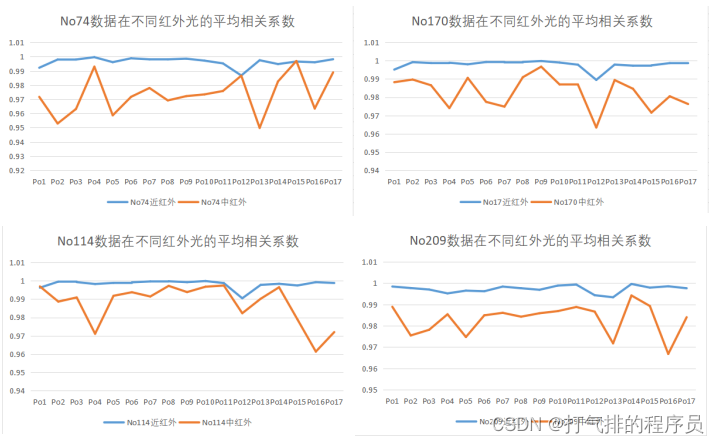
                                图 5-10 同一组未知数据在不同红外光的平均相关系数图

        分析了10组未知数据在不同红外光的平均相关系数并绘制折线图，利用同一未知产地的中红外、近红外平均相关系数差异较大的红外光作为区分10组未知数据产地的标准。(如上10组折线图可分析以中红外数据为标准)

     表 5-4 中红外光谱已知产地与未知产地最大的平均相关系数表

	No4	No15	No22	No30	No34
最大平均相关系数	0.98854	0.99812	0.99728	0.99695	0.99566

	No45	No74	No114	No170	No209
最大平均相关系数	0.99169	0.99695	0.99742	0.99674	0.99422

        表5-5 近红外光谱已知产地与未知产地最大的平均相关系数表

	No4	No15	No22	No30	No34
最大平均相关系数	0.99958	0.99954	0.99827	0.99976	0.99974

	No45	No74	No114	No170	No209
最大平均相关系数	0.99941	0.99965	0.99989	0.99984	0.99964

注释：精确到小数点后5位数

如图、如表所示：

        通过对中红外和近红外光谱的模型图和表格分析，发现已知产地与未知产地的中红外平均相关系数在同一中药材产地数据更加明显，差值相比近红外平均相关系数大，所以中红外更易区分中药材的产地，就利用中红外的数据对中药材进行分析。

见附录4，通过对已知产地与未知产地最大的中红外平均相关系数可分析得出未知产地的所属产地如表5-6所示。

No	4	15	22	30	34	45	74	114	170	209
OP	17	11	8	13	16	6	15	11	9	14

表5-6 该种药材产地的鉴别结果

以下是四种形式的神经网络：拟合/分类/聚类/时间序列

图 5-11 拟合/分类/聚类/时间序列图

输入数据集，划分训练集、反复测试集，可以看到聚类分析的准确率为87.0%，较高，分类效果不错。下表是BP神经网络演算出的结果如表5-7所示。

No	4	15	22	30	34	45	74	114	170	209
OP	10	6	1	13	10	12	6	11	13	11

表5-7 BP神经网络演算该种药材产地的鉴别结果

5.4 问题四

针对问题四，首先我们根据附件4的近红外光谱数据做分析，从附件4中观察到一共有A、B、C，3种药材类别，用Python从中把A、B、C三类含药材产地的各项数据列出来并且求出近红外光谱平均相关系数，同理，用皮尔森相关系数rxy2，建立数学模型。

     (16)

同理利用Python计算出附件4中‘已知数据’（知道已知产地和药材类型）和两组‘未知数据’（不知道已知产地和药材类型）的数据进行平均相关系数的计算，借助EXCEL统计出了‘已知数据’和‘未知数据’的平均相关系数，其图示如图5-12所示，未知药材与已知药材的最大平均相关系数表如表5-6所示。

图 5-12 未知药材与已知药材的平均相关参数图

表 5-8 未知药材与已知药材的最大平均相关系数表

	No94	No109	No140	No278	No308	No330	No347
最大平均相关系数	0.99941	0.99951	0.99953	0.99824	0.99779	0.99453	0.99420

注释：精确到小数点后5位数

见附录5，通过采用‘两组已知数据’（知道已知产地和药材类型）和‘两组未知数据’（不知道已知产地和药材类型）的数据进行平均相关系数的计算，

可分析鉴别药材的类别与所属产地如表5-6所示。

                                                表 5-9鉴别药材的类别与产地表

NO	94	109	140	278	308	330	347
Class	A	A	A	C	C	C	B
OP	2	2	2	1	3	4	10

图 5-11 拟合/分类/聚类/时间序列图

                                       表5-7 BP神经网络演算该种药材产地的鉴别结果

No	4	15	22	30	34	45	74	114	170	209
OP	10	6	1	13	10	12	6	11	13	11

5.4 问题四

        针对问题四，首先我们根据附件4的近红外光谱数据做分析，从附件4中观察到一共有A、B、C，3种药材类别，用Python从中把A、B、C三类含药材产地的各项数据列出来并且求出近红外光谱平均相关系数，同理，用皮尔森相关系数rxy2，建立数学模型。

     (16)

        同理利用Python计算出附件4中‘已知数据’（知道已知产地和药材类型）和两组‘未知数据’（不知道已知产地和药材类型）的数据进行平均相关系数的计算，借助EXCEL统计出了‘已知数据’和‘未知数据’的平均相关系数，其图示如图5-12所示，未知药材与已知药材的最大平均相关系数表如表5-6所示。

图 5-12 未知药材与已知药材的平均相关参数图

表 5-8 未知药材与已知药材的最大平均相关系数表

	No94	No109	No140	No278	No308	No330	No347
最大平均相关系数	0.99941	0.99951	0.99953	0.99824	0.99779	0.99453	0.99420

注释：精确到小数点后5位数

        见附录5，通过采用‘两组已知数据’（知道已知产地和药材类型）和‘两组未知数据’（不知道已知产地和药材类型）的数据进行平均相关系数的计算，

可分析鉴别药材的类别与所属产地如表5-6所示。

表 5-9鉴别药材的类别与产地表

NO	94	109	140	278	308	330	347
Class	A	A	A	C	C	C	B
OP	2	2	2	1	3	4	10

六、模型评价与改进

6.1 模型的优缺点

一．优点:

1.运用了正确的处理发放，选用Python编程，具有一定的实际价值。

2.模型结合Excel办公软件求解，使问题的解决简单清晰，利与读者的理解与分析。

3.模型适用性较强，适用于很多模型的求解，比较经典。

二．缺点:

1.可以适当的优化与转换，使模型变得相对复杂。

2.计算量较大，需要的数据较多。

3.模型的几个问题设置的比较接近，可以适当转变问题的思路。

4.需要有一定的训练集。

6.2 模型的改进

以效率和满意度函数做多目标规划，求得可能的最优解集，其次，从解集里寻求最优解。

1. means聚类问题，假设有一组N个数据的集合X={x1，x2，x3，…，xn}待聚类。K均值值聚类问题是要找到X的一个划分Pk={C1，C2，C3，…，Ck}，使目标函数f（Pk）=1(,)iikiiixcdxm=∈∑∑最小。
   其中，mi=1/ni，iiixcx∈∑表示第i个簇中心位置，i=1，…，k；ni是簇Ci中数据项的个数；(,)iidxm表示xi到mi的距离。
   通常的空间聚类算法是建立在各种距离基础上的，如欧几里得距离、曼哈顿距离和明考斯距离等。其中，最常用的是欧几里得距离。
   
       改进的K-means算法：K-means与ISODATA：ISODATA的全称是迭代自组织数据分析法。
       在K-means中，K的值需要预先人为地确定，并且在整个算法过程中无法更改。而当遇到高维度、海量的数据集时，人们往往很难准确地估计出K的大小。
   ISODATA就是针对这个问题进行了改进，它的思想也很直观：
   当属于某个类别的样本数过少时把这个类别去除，当属于某个类别的样本数过多、分散程度较大时把这个类别分为两个子类别。

BP网络的训练需要较长时间;完全不能训练时,选取较小的初始权值,采用较小的学习速率,但同时又增加了训练时间;BP网络的训练容易落到局部极值;BP算法可以使网络权值收敛到一个解,但它并不能保证所求为误差超平面的全局最小解,很可能是一个局部极小解。

七、参考文献

[1]宋争艳,王振坤,尹奕,李厚彪.基于K-means聚类分析的任务定价方案[J].实验科学与技术.2019(02)

[2]卓金武.MATLAB在数学建模中的应用[M].北京：北京航空航天大学出版社，2014.

[3]赵静，但琦.数学建模与数学实验[M].北京：高等教育出版社，2000.

[4]王晓丽.基于光谱分析技术的果树花、叶理化性状信息提取及建模[D].北京林业大学2017

[5]林加剑,韦天下,施国栋,王朝成,王辉,周理洋.准静态玄武岩纤维混凝土力学性能及其BP神经网络预测模型研究[J].防护工程.2020(06)

[6]刘全.近红外光谱技术在中药生产过程质量分析中的应用研究[D].浙江大学2004

[7]近红外光谱分析基础与应用[M].中国轻工业出版社,严衍禄主编,2005

[8]王玲,刘焕良,张丽华,范德军,钱红娟,王铁健,李定明,吴继宗.可见光谱-偏最小二乘法同时快速分析U（Ⅳ）、U（Ⅵ）含量[J].中国原子能科学研究院年报.2015(00)

[9]张晓华,张骥,汤秀章.空间偏移拉曼光谱新技术研究[J].中国原子能科学研究院年报.2013(00)

[10]黄必胜,袁明洋,余驰,刘义梅,陈科力.基于近红外特征谱段相关系数法鉴别真伪龙齿[J].中国药师.2014(04)

[11]李波霞,魏玉辉,席莉莉,段好刚,武新安.近红外光谱和化学计量学对不同产地不同产期当归的定性研究[J].光谱实验室.2011(04)

八、附录清单

附录1：问题一程序代码（Python）

import pandas as pd
import matplotlib.pyplot as plt
# 相对路径下，直接输入文件名
data = pd.read_excel("1.xlsx")
data
# X轴
x = data.columns.tolist()[1:]
x
plt.figure(figsize=(20, 20))
for index in range(len(data)):
    # 所有的Y轴数据
    y = data.iloc[index, :].values.tolist()[1:]
    plt.plot(x, y)
plt.show()

问题二、程序代码（Python）

import pandas as pd
def relative_R(list_df):
    //
    :param list_df: list
    :return: 相关系数和执行次数
    计算平均相关系数
    //
    list_R = []  # 装载处理后的相关系数
    blank_collection = list_df[-1].iloc[:, 3:].T
    s = 0
    for number in range(15):  # 未知的15个场地
        n = 100 + number
        blank_df = pd.DataFrame(blank_collection[number])
        blank_df = blank_df.rename(columns={number: n})
        for place in list_df[:-1]:  # 已知的11类场地
            s += 1
            place = place.iloc[:, 3:].T
            cct = pd.concat([place, blank_df], axis=1)
            R_LIST = cct.corr()[n][:-1]
            list_R.append(cct.corr()[n][:-1].sum() / len(R_LIST))
    return list_R, "执行次数：{}".format(s)


if __name__ == '__main__':
    data = pd.read_excel("附件2.xlsx")
    # print(data)
    data['OP'] = data['OP'].fillna(value=12)  # 将表中的空白数据填充为12， 方便后续工作

    df = []  #
    for i in data.groupby(data['OP']):
        i = pd.DataFrame(i[1]).reset_index()
        df.append(i)  # 将处理好的数据添加到list_df中

    # 调用函数
    R = relative_R(df)[0]  # 返回相关系数
    TIME = relative_R(df)[1]  # 返回执行次数，也就是相关系数的个数

    p1 = 0
    p2 = 11
    unknown = 1
    while p2 <= 165:
        m = max(list(R[p1:p2]))
        print("已知的11类场地分别与未知场地{}的平均相关系数的最大值为：".format(unknown), m)
        p2 += 11
        p1 += 11
        unknown += 1

问题三 程序代码（Python）

import pandas as pd

data = pd.read_excel("问题3中红外.xlsx")

data['OP'] = data['OP'].fillna(value=20)  # 将未知场地的标为20，方便后续工作

data_gp = data.groupby(data['OP'])  # 以场地为基准分组数据
data_gp_list = []  # 存储分类后的数据
for op in data_gp:
    deel = op[1].reset_index().iloc[:, 3:].T  # 取出要用的数据并转置
    data_gp_list.append(deel)  # 添加到data_gp_list

data_gp_list_17 = data_gp_list[:-1]  # 取出17类已知产地
data_gp_list_10 = data_gp_list[-1]  # 取出10个未知场地

# Rmean_list_10：未知场地和已知场地各自分别的相关系数的平均值，一共为10组，每组17个
Rmean_list_10 = [[], [], [], [], [], [], [], [], [], []]
for number in range(10):  # 未知的10个场地
    x = pd.DataFrame(data_gp_list_10[number]).rename(columns={number: 20})
    for place in data_gp_list_17:  # 已知的17类场地
        cct = pd.concat([place, x], axis=1)
        R = cct.corr()[20][:-1]  # 调用corr函数计算相关性, 因为最后一列为未知的场地,所以选取的列名为20的列，去除最后一个的自我比较
        Rmean = R.mean()
        Rmean_list_10[number].append(Rmean)
# print(Rmean_list_10)

df_Rmean_list_10 = pd.DataFrame(Rmean_list_10)  # 将df_Rmean_list_10转为DataFrame
df_Rmean_list_10.to_excel("df_Rmean.xlsx")  # 保存文件

九、文档吧、附录清单、附件下载

下载链接：2021年高教社杯全国大学生数学建模竞赛《中药材的鉴别》资源-CSDN文库