文章目录
1.方程
1.1“和”形式
f
k
(
s
k
)
=
o
p
t
p
k
∈
P
K
(
s
k
)
n
{
R
k
(
s
k
,
p
k
(
s
k
)
)
}
=
o
p
t
{
∑
i
=
k
n
g
i
(
s
i
,
u
i
)
}
f_k(s_k)=\mathop{opt}\limits_{p_k\in P_K(s_k)}^n\{R_k(s_k,p_k(s_k))\}=opt\{\sum_{i=k}^ng_i(s_i,u_i)\}
fk(sk)=pk∈PK(sk)optn{Rk(sk,pk(sk))}=opt{i=k∑ngi(si,ui)}
相应函数基本方程为
{
f
n
+
1
(
s
n
+
1
)
=
β
,
f
k
(
s
k
)
=
o
p
t
u
k
∈
U
k
{
g
k
(
s
k
,
u
k
(
s
k
)
)
+
f
k
+
1
(
s
k
+
1
)
}
,
k
=
n
,
n
−
1
,
⋯
,
2
,
1
\left\{ \begin{array}{l} f_{n+1}(s_{n+1})=\beta, \\ f_k(s_k)=\mathop{opt}\limits_{u_k\in U_k}\{g_k(s_k,u_k(s_k))+f_{k+1}(s_{k+1})\},\\ k=n,n-1,\cdots,2,1 \end{array} \right.
⎩
⎨
⎧fn+1(sn+1)=β,fk(sk)=uk∈Ukopt{gk(sk,uk(sk))+fk+1(sk+1)},k=n,n−1,⋯,2,1
1.2“积”形式
f
k
(
s
k
)
=
o
p
t
∏
p
k
∈
P
K
(
s
k
)
n
{
R
k
(
s
k
,
p
k
(
s
k
)
)
}
=
o
p
t
{
∑
i
=
k
n
g
i
(
s
i
,
u
i
)
}
f_k(s_k)=\mathop{opt}\prod_{p_k\in P_K(s_k)}^n\{R_k(s_k,p_k(s_k))\}=opt\{\sum_{i=k}^ng_i(s_i,u_i)\}
fk(sk)=optpk∈PK(sk)∏n{Rk(sk,pk(sk))}=opt{i=k∑ngi(si,ui)}
相应函数基本方程为
{
f
n
+
1
(
s
n
+
1
)
=
α
f
k
(
s
k
)
=
o
p
t
u
k
∈
U
k
{
g
k
(
s
k
,
u
k
(
s
k
)
)
⋅
f
k
+
1
(
s
k
+
1
)
}
k
=
n
,
n
−
1
,
⋯
,
2
,
1
\left\{\begin{array}{lr} f_{n+1}(s_{n+1})=\alpha\\ f_k(s_k)=\mathop{opt}\limits_{u_k\in U_k}\{g_k(s_k,u_k(s_k))\cdot f_{k+1}(s_{k+1})\}\\ k=n,n-1,\cdots,2,1 \end{array} \right.
⎩
⎨
⎧fn+1(sn+1)=αfk(sk)=uk∈Ukopt{gk(sk,uk(sk))⋅fk+1(sk+1)}k=n,n−1,⋯,2,1
常用求最小加法计算公式:
{
f
n
+
1
(
s
n
+
1
)
=
0
;
边界条件
f
k
(
s
k
)
=
m
i
n
u
k
∈
U
k
(
s
k
)
{
g
k
(
s
k
,
u
k
(
s
k
)
)
+
f
k
+
1
(
s
k
+
1
)
}
;
阶段指标
k
=
1
,
n
−
1
,
⋯
,
2
,
1
\left\{\begin{array}{lr} f_{n+1}(s_{n+1})=0; 边界条件\\ f_k(s_k)=\mathop{min} \limits_{u_k\in U_k(s_k)}\{g_k(s_k,u_k(s_k))+f_{k+1}(s_{k+1})\};阶段指标\\ k=1,n-1,\cdots,2,1 \end{array} \right.
⎩
⎨
⎧fn+1(sn+1)=0;边界条件fk(sk)=uk∈Uk(sk)min{gk(sk,uk(sk))+fk+1(sk+1)};阶段指标k=1,n−1,⋯,2,1
2.基本思想和解题步骤
逆推求解
- 建立动态规划模型
- 递推求解基本方程
- 回溯
**合理、有效建立模型**
3.问题实例
3.1最短路径问题
3.1.1标号法——最优路线问题
- 给最后一段标号
- 向前递推
- 逐次向前递推
下图中一货运汽车从 S 出发,最终到达目的地 E 。其中,
A
i
(
i
=
1
,
2
,
3
)
A_i (i=1, 2, 3)
Ai(i=1,2,3),
B
j
(
j
=
1
,
2
)
B_j (j=1, 2)
Bj(j=1,2) 和
C
k
(
k
=
1
,
2
)
C_k (k=1, 2)
Ck(k=1,2)是可供汽车选择的途经站点,各点连线上的数字表示两站点间的距离。
问此汽车应走哪条路线,使所经过的路程距离最短?
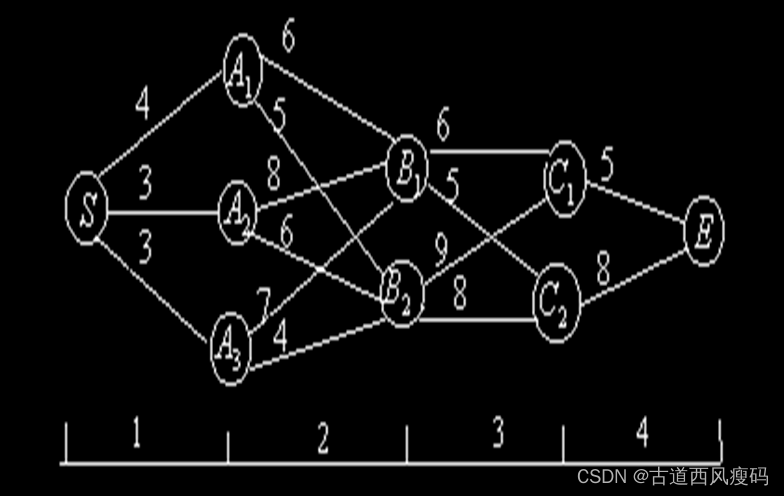
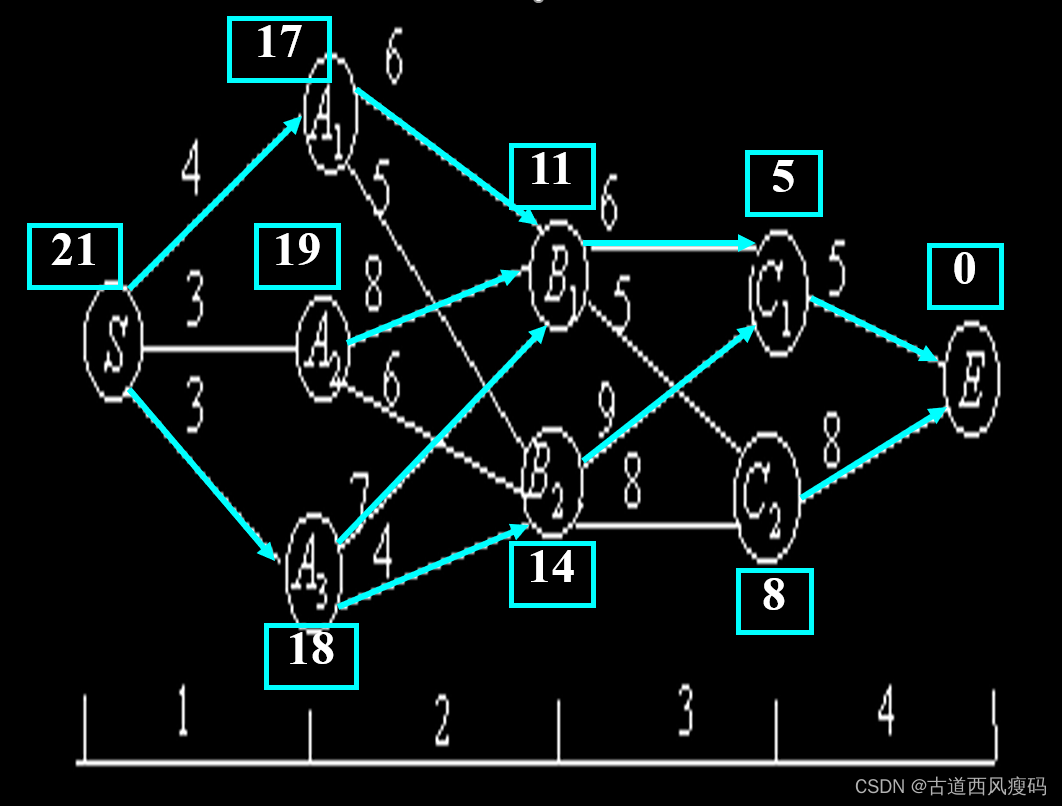
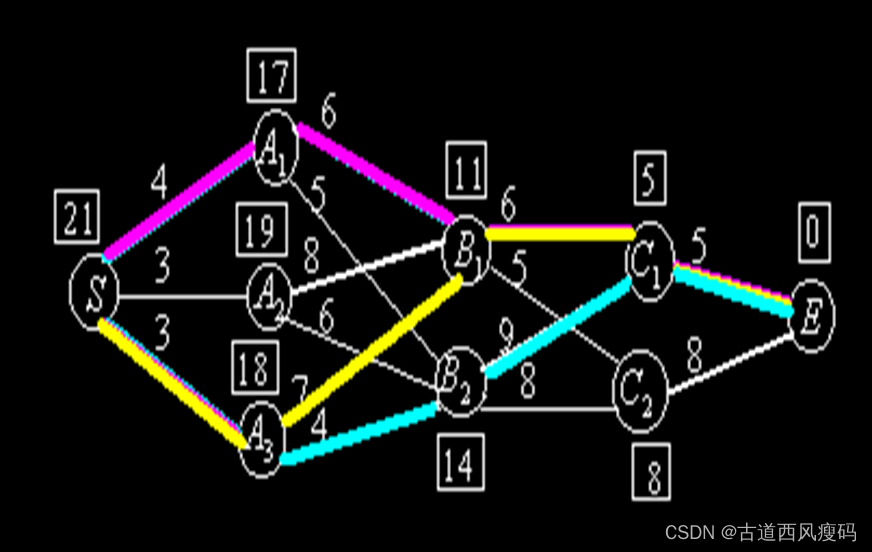
从S到E最短距离为21,共有三条最短路线:
- S → A 1 → B 1 → C 1 → E S\rightarrow A_1 \rightarrow B_1 \rightarrow C_1 \rightarrow E S→A1→B1→C1→E
- S → A 3 → B 1 → C 1 → E S\rightarrow A_3 \rightarrow B_1 \rightarrow C_1\rightarrow E S→A3→B1→C1→E
- S → A 3 → B 2 → C 1 → E S\rightarrow A_3\rightarrow B_2\rightarrow C_1\rightarrow E S→A3→B2→C1→E
3.1.2表格法
当问题不便于表示为网络图形式时,标号法会失去作用。离散型问题的递推公式往往无法表示为解析式,因此运算过程使用表格较为方便.(就本人意见来说,这种方法只适合于少量节点问题,因为其本质仍是一种枚举法,因此并不推崇)
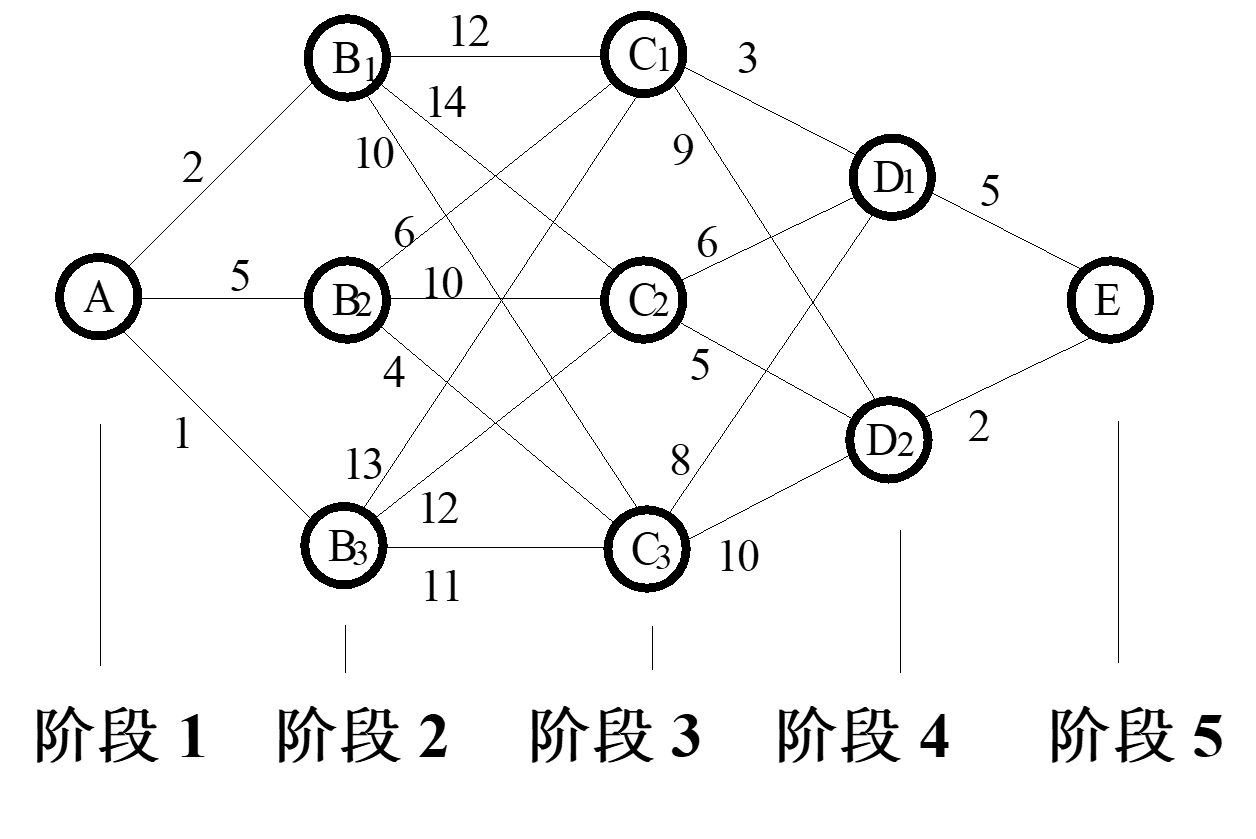
建模
(1)如图划分成 5 个阶段。
(2)状态变量
x
k
x_k
xk表示第
k
k
k阶段开始的位置。
(3)决策变量
d
k
d_k
dk定义为到达下一站所选择的路径。
(4)状态转移:决策确定了下一阶段的状态。
(5)阶段指标:图中线段上所标的数值。
(6)最优指标函数
f
k
(
x
k
)
f_k(x_k)
fk(xk):
f
k
(
x
k
)
=
m
i
n
d
k
∈
D
k
(
x
k
)
{
v
k
(
x
k
,
d
k
)
+
f
k
+
1
(
x
k
+
1
)
}
(
k
=
4
,
3
,
2
,
1
)
f_k(x_k)=\mathop{min}\limits_{d_k\in D_k(x_k)}\{v_k(x_k,d_k)+f_{k+1}(x_{k+1})\}\\ (k=4,3,2,1)
fk(xk)=dk∈Dk(xk)min{vk(xk,dk)+fk+1(xk+1)}(k=4,3,2,1)
终端条件为
f
5
(
x
5
)
=
f
5
(
E
)
=
0
f_5(x_5)=f_5(E)=0
f5(x5)=f5(E)=0,其含义为从E到E的最短路径为0.
第四阶段的递推:
f
4
(
x
4
)
=
m
i
n
d
4
∈
D
4
(
x
4
)
{
v
4
(
x
4
,
d
4
)
+
f
5
(
x
5
)
}
f_4(x_4)=\mathop{min}\limits_{d_4\in D_4(x_4)}\{v_4(x_4,d_4)+f_{5}(x_{5})\}
f4(x4)=d4∈D4(x4)min{v4(x4,d4)+f5(x5)}从
f
5
(
x
5
)
f_5(x_5)
f5(x5)到
f
4
(
x
4
)
f_4(x_4)
f4(x4)的递推过程:
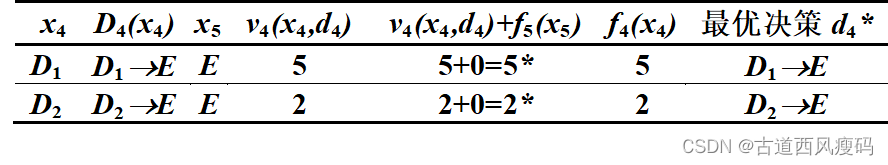
第三阶段的递推:
f
3
(
x
3
)
=
m
i
n
d
3
∈
D
3
(
x
3
)
{
v
3
(
x
3
,
d
3
)
+
f
4
(
x
4
)
}
f_3(x_3)=\mathop{min}\limits_{d_3\in D_3(x_3)}\{v_3(x_3,d_3)+f_{4}(x_{4})\}
f3(x3)=d3∈D3(x3)min{v3(x3,d3)+f4(x4)}从
f
4
(
x
4
)
f_4(x_4)
f4(x4)到
f
3
(
x
3
)
f_3(x_3)
f3(x3)的递推过程:

第2阶段的递推方程为:
f
2
(
x
2
)
=
m
i
n
d
2
∈
D
2
(
x
2
)
{
v
2
(
x
2
,
d
2
)
+
f
3
(
x
3
)
}
f_2(x_2)=\mathop{min}\limits_{d_2\in D_2(x_2)}\{v_2(x_2,d_2)+f_{3}(x_{3})\}
f2(x2)=d2∈D2(x2)min{v2(x2,d2)+f3(x3)}从
f
3
(
x
3
)
f_3(x_3)
f3(x3)到
f
2
(
x
2
)
f_2(x_2)
f2(x2)的递推过程:

第1阶段的递推方程为:
f
1
(
x
1
)
=
m
i
n
d
1
∈
D
1
(
x
1
)
{
v
1
(
x
1
,
d
1
)
+
f
2
(
x
2
)
}
f_1(x_1)=\mathop{min}\limits_{d_1\in D_1(x_1)}\{v_1(x_1,d_1)+f_{2}(x_{2})\}
f1(x1)=d1∈D1(x1)min{v1(x1,d1)+f2(x2)}从
f
2
(
x
2
)
f_2(x_2)
f2(x2)到
f
1
(
x
1
)
f_1(x_1)
f1(x1)的递推过程:
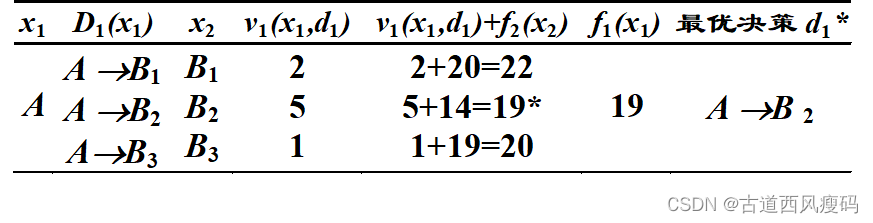
由此得到
f
1
(
x
1
)
=
19
f_1(x_1) =19
f1(x1)=19 , 即从
A
A
A 到
E
E
E的最短路径长度为19。
回溯求最优策略:
由
f
1
(
x
1
)
f_1(x_1)
f1(x1) 向
f
4
(
x
4
)
f_4(x_4)
f4(x4) 回溯,得到最短路径为:
A
→
B
2
→
C
1
→
D
1
→
E
A\rightarrow B_2\rightarrow C_1\rightarrow D_1\rightarrow E
A→B2→C1→D1→E
3.2资源分配问题
现有资金 4 万元,投资
A
、
B
、
C
A、B、C
A、B、C 三个项目,每个项目的投资效益与投入该项目的资金有关。三个项目
A
、
B
、
C
A、B、C
A、B、C 的投资效益(万
t
t
t)和投入资金(万元)关系见下表:

求最优投资分配使总投资效益最大。
建模:
(1) 阶段
k
k
k:每投资一个项目作为一个阶段。
(2) 状态变量
x
k
x_k
xk:投资第
k
k
k(
k
=
A
,
B
,
C
k=A,B,C
k=A,B,C)个项目前的资金。(指包括第
k
k
k(
k
=
A
,
B
,
C
k=A,B,C
k=A,B,C)个项目在内之后的项目可用资金)
(3) 决策变量
d
k
d_k
dk:第
k
k
k个项目的投资。决策允许集合:
0
≤
d
k
≤
x
k
0≤d_k≤x_k
0≤dk≤xk
(4) 状态转移方程:
x
k
+
1
=
x
k
−
d
k
x_{k+1}=x_k-d_k
xk+1=xk−dk。
(5) 阶段指标:
v
k
(
x
k
,
d
k
)
v_k(x_k ,d_k)
vk(xk,dk)见表中所示。
(6) 递推方程:
f
k
(
x
k
)
=
m
a
x
{
v
k
(
x
k
,
d
k
)
+
f
k
+
1
(
x
k
+
1
)
}
f_k(x_k)=max\{v_k(x_k ,d_k)+f_{k+1}(x_{k+1})\}
fk(xk)=max{vk(xk,dk)+fk+1(xk+1)}
终端条件:
f
4
(
x
4
)
=
0
f_4(x_4)=0
f4(x4)=0
求解基本方程:
k
=
4
,
f
4
(
x
4
)
=
0
,
k
=
3
,
0
≤
d
3
≤
x
3
,
x
4
=
x
3
−
d
3
k=4,f_4(x_4)=0, k=3,0≤d_3≤x_3,x_4=x_3-d_3
k=4,f4(x4)=0,k=3,0≤d3≤x3,x4=x3−d3
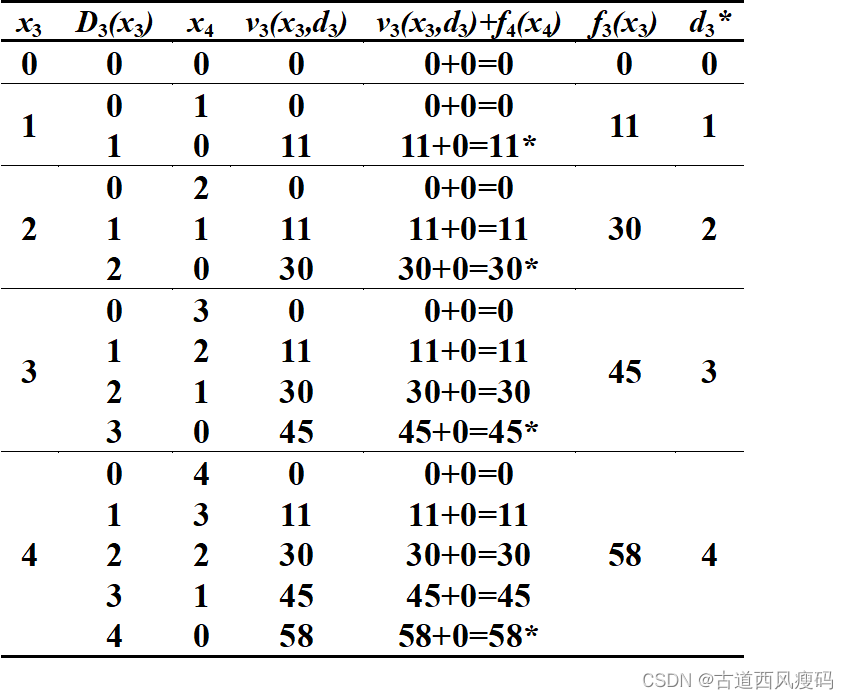
k
=
2
,
0
≤
d
2
≤
x
2
,
x
3
=
x
2
−
d
2
k=2,0≤d_2≤x_2,x_3=x_2-d_2
k=2,0≤d2≤x2,x3=x2−d2

k
=
1
,
0
≤
d
1
≤
x
1
,
x
2
=
x
1
-
d
1
k=1,0≤d_1≤x_1,x_2=x_1-d_1
k=1,0≤d1≤x1,x2=x1-d1

回溯,求得最优解为
x
1
=
4
,
d
1
∗
=
1
,
x
2
=
x
1
−
d
1
=
3
,
d
2
∗
=
0
,
x
3
=
x
2
−
d
2
∗
=
3
,
d
3
=
3
,
x
4
=
x
3
−
d
3
=
0
x_1=4, d_1^*=1, x_2=x_1-d_1=3, d_2^*=0, x_3=x_2-d_2^*=3, d_3=3, x_4=x_3-d_3=0
x1=4,d1∗=1,x2=x1−d1=3,d2∗=0,x3=x2−d2∗=3,d3=3,x4=x3−d3=0,
即项目A投资1万元,项目B投资0万元,项目C投资3万元,最大效益为60万t。
3.3连续型动态规划问题
当状态变量和决策变量的取值范围很大,或者这些变量是连续时,用列举的方法就比较困难或者根本不可能。
机器负荷分配问题
某机器可以在高、低两种负荷下生产。高负荷生产条件下机器完好率为0.7,单台产量为8t;低负荷运行时,机器完好率为0.9,单台产量为5t。设开始时有1000台完好机器,要制订五年计划,每年年初将完好的机器一部分分配到高负荷生产,剩下的机器分配到低负荷生产,使五年的总产量为最高。
注:完好率,年初投入生产年末保持完好的机器数量比率;单台产量,年初运行机器的平均年产量。
构造动态规划模型如下:
(1) 阶段k:运行年份
(
k
=
1
,
2
,
3
,
4
,
5
,
6
)
(k =1, 2, 3, 4, 5, 6)
(k=1,2,3,4,5,6),其中
k
=
1
k =1
k=1表示第1年初,
⋯
\cdots
⋯,
k
=
6
k = 6
k=6表示第6年初(即第5年末)。
(2) 状态变量
x
k
x_k
xk:第
k
k
k 年初完好的机器数
(
k
=
1
,
2
,
3
,
4
,
5
,
6
)
(k =1, 2, 3, 4, 5, 6)
(k=1,2,3,4,5,6),其中
x
6
x_6
x6表示第5年末(即第6年初)的完好机器数。
(3) 决策变量
d
k
d_k
dk:第
k
k
k年投入高负荷运行的机器数;
(4) 决策允许集合:
D
k
(
x
k
)
=
{
d
k
∣
0
≤
d
k
≤
x
k
}
D_k(x_k)=\{d_k|0\leq d_k\leq x_k\}
Dk(xk)={dk∣0≤dk≤xk}
(5) 状态转移方程:
x
k
+
1
=
0.7
d
k
+
0.9
(
x
k
−
d
k
)
x_{k+1}=0.7d_k+0.9(x_k-d_k)
xk+1=0.7dk+0.9(xk−dk)
(6) 阶段指标:
v
k
(
x
k
,
d
k
)
=
8
d
k
+
5
(
x
k
−
d
k
)
v_k(x_k , d_k) =8d_k+5(x_k-d_k)
vk(xk,dk)=8dk+5(xk−dk)
(7) 终端条件:
f
6
(
x
6
)
=
0
f_6(x_6) = 0
f6(x6)=0
(8) 递推方程:
f
k
(
x
k
)
=
m
a
x
d
k
∈
D
k
(
x
k
)
{
v
k
(
x
k
,
d
k
)
+
f
k
+
1
(
x
k
+
1
)
}
=
m
a
x
d
k
∈
D
k
(
x
k
)
{
8
d
k
+
5
(
x
k
−
d
k
)
+
f
k
+
1
[
0.7
d
k
+
0.9
(
x
k
−
d
k
)
]
}
0
≤
d
k
≤
x
k
\begin{aligned} f_k(x_k) &= \mathop{max}\limits_{d_k\in D_k(x_k)}\{v_k(x_k,d_k)+f_{k+1}(x_{k+1})\} \\ &= \mathop{max}\limits_{d_k\in D_k(x_k)}\{8d_k+5(x_k- d_k)+f_{k+1}[0.7d_k+0.9(x_k-d_k)]\}\\ &0\leq d_k\leq x_k \end{aligned}
fk(xk)=dk∈Dk(xk)max{vk(xk,dk)+fk+1(xk+1)}=dk∈Dk(xk)max{8dk+5(xk−dk)+fk+1[0.7dk+0.9(xk−dk)]}0≤dk≤xk
本题的决策允许集合应是一个整数集合,但由于决策允许集合中可取的决策数量很大,一一列举计算量也很大,不妨认为状态变量和决策变量都是连续的,得到最优解后,再作取整处理。
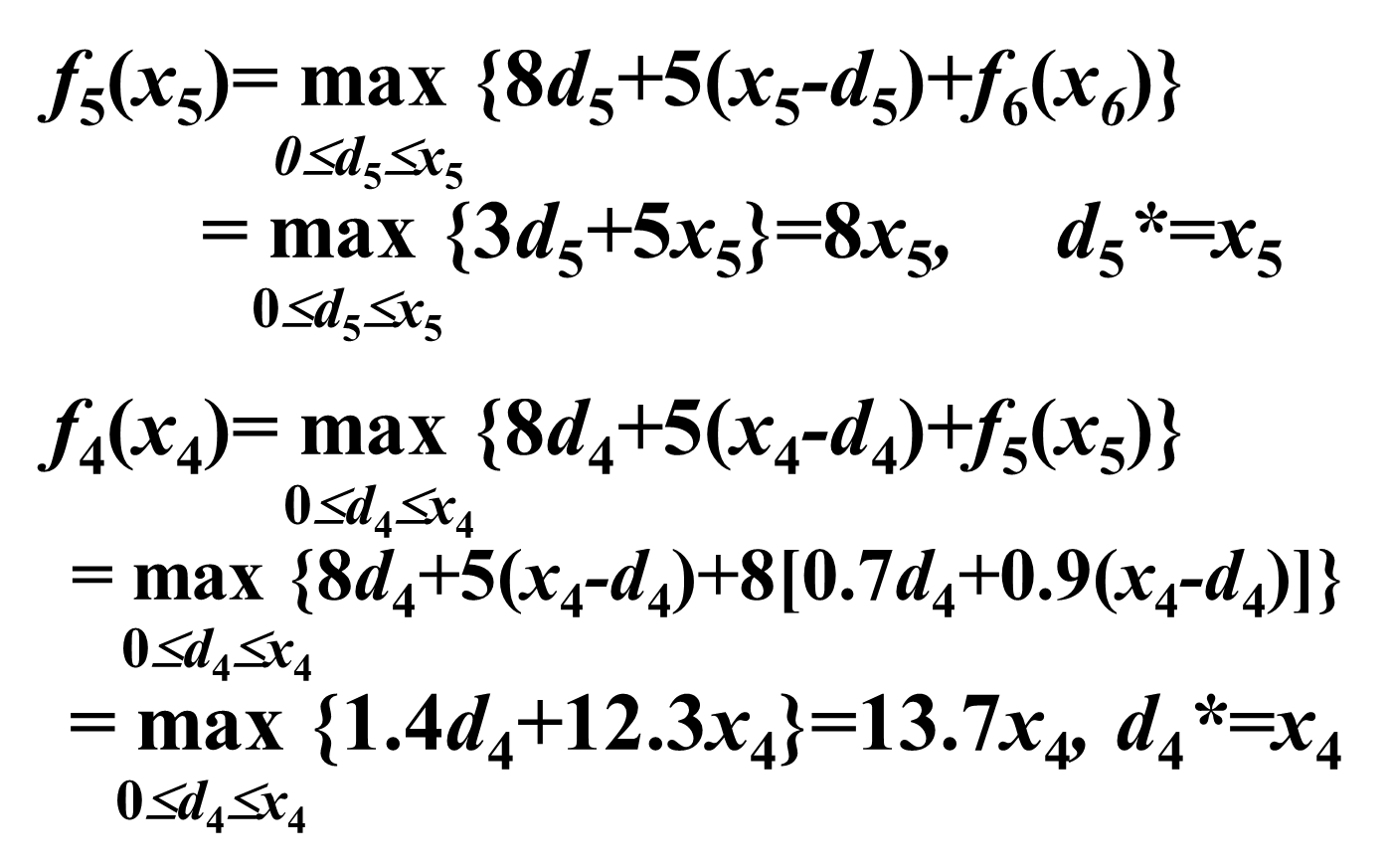
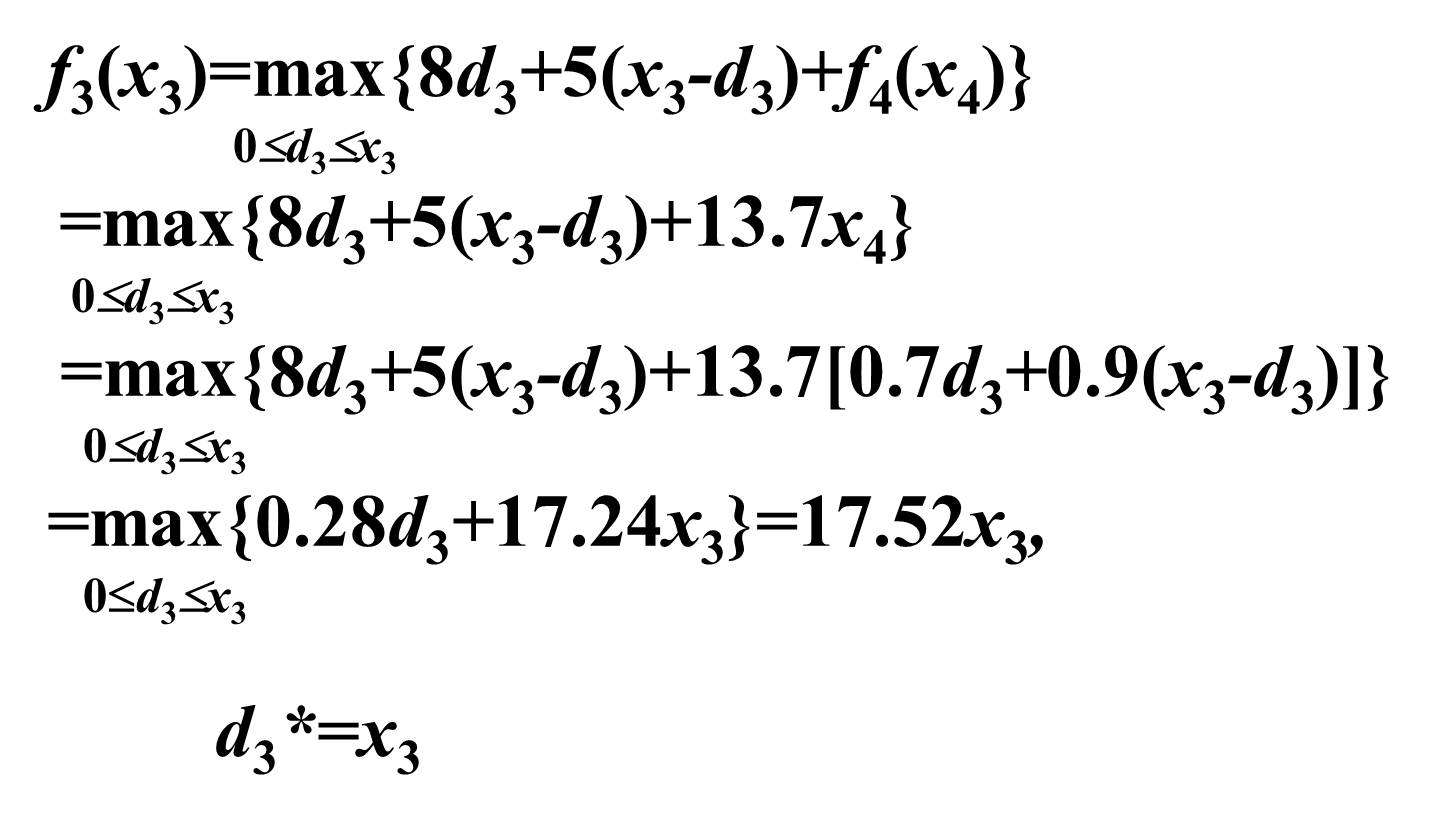
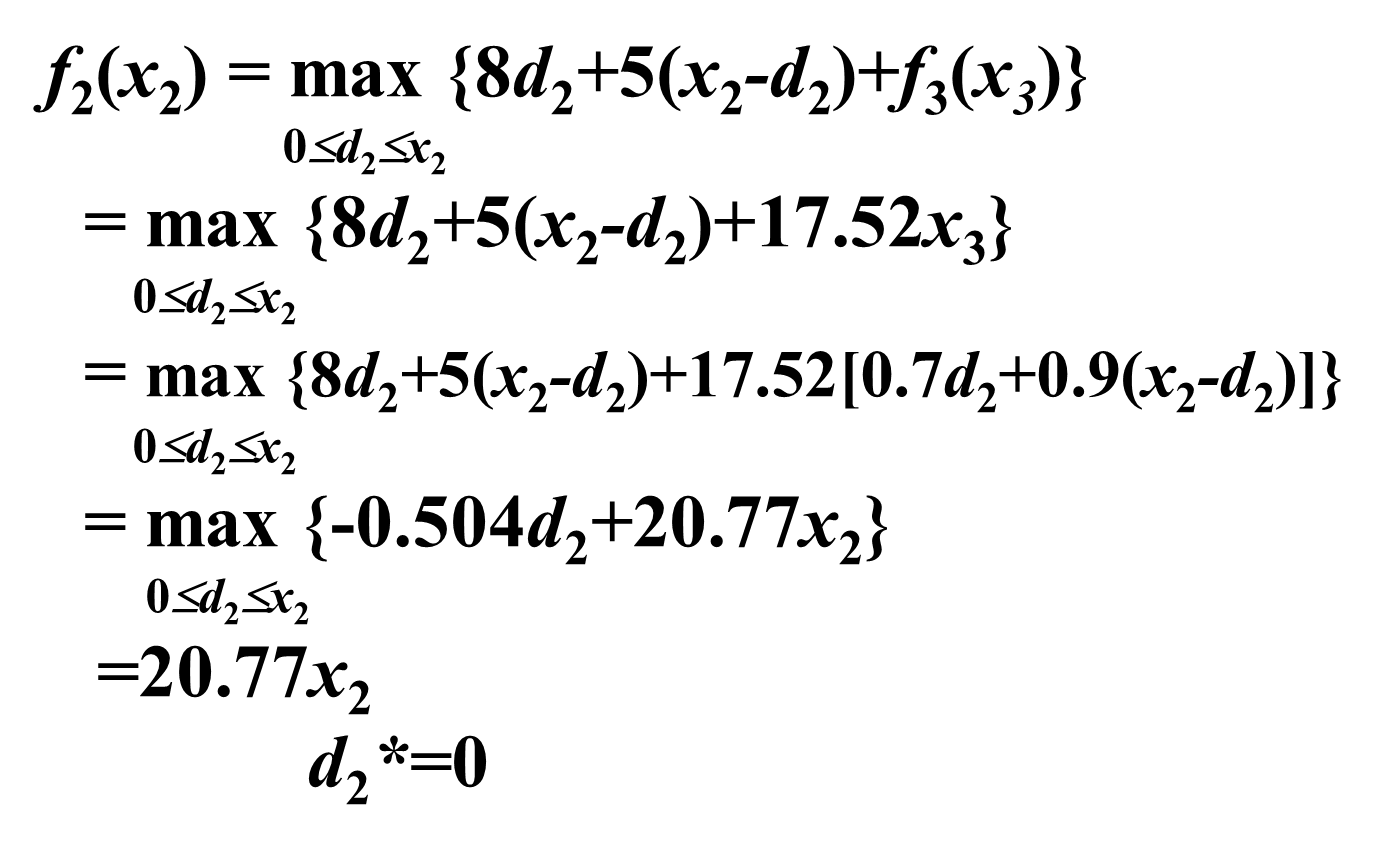

回溯,可以得到:
f
1
(
x
1
)
=
23.69
x
1
,
d
1
∗
=
0
f
2
(
x
2
)
=
20.77
x
2
,
d
2
∗
=
0
f
3
(
x
3
)
=
17.52
x
3
,
d
3
∗
=
x
3
f
4
(
x
4
)
=
13.60
x
4
,
d
4
∗
=
x
4
f
5
(
x
5
)
=
8
x
5
,
d
5
∗
=
x
5
f_1(x_1)=23.69x_1, d_1*=0\\ f_2(x_2)=20.77x_2, d_2*=0\\ f_3(x_3)=17.52x_3, d_3*=x_3\\ f_4(x_4)=13.60x_4, d_4*=x_4\\ f_5(x_5)=8x_5,d_5*=x_5
f1(x1)=23.69x1,d1∗=0f2(x2)=20.77x2,d2∗=0f3(x3)=17.52x3,d3∗=x3f4(x4)=13.60x4,d4∗=x4f5(x5)=8x5,d5∗=x5
用
x
1
=
1000
x_1=1000
x1=1000代入,得到五年最大产量为
f
1
(
x
1
)
=
f
1
(
1000
)
=
23690
f_1(x_1)=f_1(1000)=23690
f1(x1)=f1(1000)=23690
每年投入高负荷运行的机器数以及每年初完好的机器数为:
x
1
=
1000
d
1
∗
=
0
,
x
2
=
0.7
d
1
+
0.9
(
x
1
−
d
1
)
=
900
d
2
∗
=
0
,
x
3
=
0.7
d
2
+
0.9
(
x
2
−
d
2
)
=
810
d
3
∗
=
x
3
=
810
,
x
4
=
0.7
d
3
+
0.9
(
x
3
−
d
3
)
=
567
d
4
∗
=
x
4
=
567
,
x
5
=
0.7
d
4
+
0.9
(
x
4
−
d
4
)
=
397
d
5
∗
=
x
5
=
397
,
x
6
=
0.7
d
5
+
0.9
(
x
5
−
d
5
)
=
278
x_1=1000\\ d_1^*=0, x_2=0.7d_1+0.9(x_1-d_1)=900\\ d_2^*=0, x_3=0.7d_2+0.9(x_2-d_2)=810\\ d_3^*=x_3=810, x_4=0.7d_3+0.9(x_3-d_3)=567\\ d_4^*=x_4=567, x_5=0.7d_4+0.9(x4-d_4)=397\\ d_5^*=x_5=397, x_6=0.7d_5+0.9(x_5-d_5)=278
x1=1000d1∗=0,x2=0.7d1+0.9(x1−d1)=900d2∗=0,x3=0.7d2+0.9(x2−d2)=810d3∗=x3=810,x4=0.7d3+0.9(x3−d3)=567d4∗=x4=567,x5=0.7d4+0.9(x4−d4)=397d5∗=x5=397,x6=0.7d5+0.9(x5−d5)=278
讨论
例中状态变量的终端值
x
6
x_6
x6是未加约束的,如果要求在第5年末(即第6年初)完好的机器数不少于500台,这时决策变量
d
5
d_5
d5 的决策允许集合将成为:
D
5
(
x
5
)
=
{
d
5
∣
0.7
d
5
+
0.9
(
x
5
−
d
5
)
≥
500
,
d
5
≥
0
}
即
0.9
x
5
−
0.2
d
5
≥
500
,
d
5
≥
0
或
0
≤
d
5
≤
4.5
x
5
−
2500
D_5(x_5)=\{d_5|0.7d_5+0.9(x_5-d_5)\geq500, d_5\geq0\}\\即 0.9x_5-0.2d_5\geq500 ,d5\geq0 \\ 或0 \leq d_5\leq4.5x_5-2500
D5(x5)={d5∣0.7d5+0.9(x5−d5)≥500,d5≥0}即0.9x5−0.2d5≥500,d5≥0或0≤d5≤4.5x5−2500
容易看到,这时的最大产量将比“
x
6
x_6
x6 是自由的”情况下小。
这个例子可以推广到一般情况。设高负荷生产时机器的完好率为
k
1
k_1
k1,单台产量为
p
1
p_1
p1;低负荷完好率为
k
2
k_2
k2,单台产量为
p
2
p_2
p2。若有
t
t
t满足:
∑
i
=
0
n
−
(
t
+
1
)
k
1
i
≤
p
1
−
p
2
p
1
(
k
2
−
k
1
)
≤
∑
i
=
0
n
−
t
k
1
i
\sum_{i=0}^{n-(t+1)}k_1^i\leq \frac{p_1-p_2}{p_1(k_2-k_1)}\leq \sum_{i=0}^{n-t}k_1^i
i=0∑n−(t+1)k1i≤p1(k2−k1)p1−p2≤i=0∑n−tk1i
则从 1 到
t
−
1
t-1
t−1 年,年初将全部完好机器投入低负荷运行,从
t
t
t 到
n
n
n 年,年初将全部完好机器投入高负荷运行,这样的决策将使总产量达到最大。

























 592
592











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










