目录
Change of Variable Theorem(变量变化理论)
摘要
上周学习的几种生成模型都存在一定的问题,这周学习了一种比较独特的生成模型-流模型,这个模型选择直面生成模型的概率计算,与其他生成模型不同的是,流模型可是实现两个分布之间的相互转换,这就需要对生成器加以限制,因此采用多个生成器架构形成流模型。这周首先通过了解数学背景学习流模型计算概率的方法,也就是通过雅可比行列式变换以及变量变换理论。而为了方便雅可比行列式的计算,学习了一种耦合层的设计方法。最后通过手写推导学习变量变换的原理以及简单学习了扩散模型的概念以及生成方法和四种生成模型的对比。
Abstract
The several generation models we learned last week all had certain problems. This week, we learned a unique generation model - the flow model. This model chooses to directly calculate the probability of the generation model. Unlike other generation models, the flow model can achieve mutual conversion between two distributions, which requires limitations on the generator. Therefore, multiple generator architectures are used to form the flow model. This week, we will first learn the method of calculating probability using flow models by understanding the mathematical background, that is, through Jacobian determinant transformation and variable transformation theory. In order to facilitate the calculation of Jacobian determinants, a design method for coupling layers was studied. Finally, the principle of learning variable transformation was derived through handwriting, and the concept of diffusion model and the comparison of generation methods and four generation models were simply learned.
前言
在上一周学习的三种生成模型,都存在一定的问题:
- PixelRNN的问题:它的生成是从左上角的一个像素开始的,因此就需要考虑生成顺序是否合理,而RNN生成的每一个像素是否只与前面的像素有关,因此这就是PixelRNN的问题所在。
- VAE的问题:它的生成只是在模仿,例如生成图片的时候,生成的图片是由真实图片的线性组合得到,没有做到真正的“创造"。
- GAN的问题:虽然GAN做到了真正的”创造”,可以算是生成模型里最好的一个模型,但是它的训练太难了。
实际上生成器G是一个神经网络,其定义了一个概率分布,例如下图,输入为Z,可以看成是从一个normal distribution即正态分布中采样得来的,经过生成器网络得到一个分布,其中x可以称为观测变量,也就是实际上可以得到的样本,而观测变量x的真实分布为
。
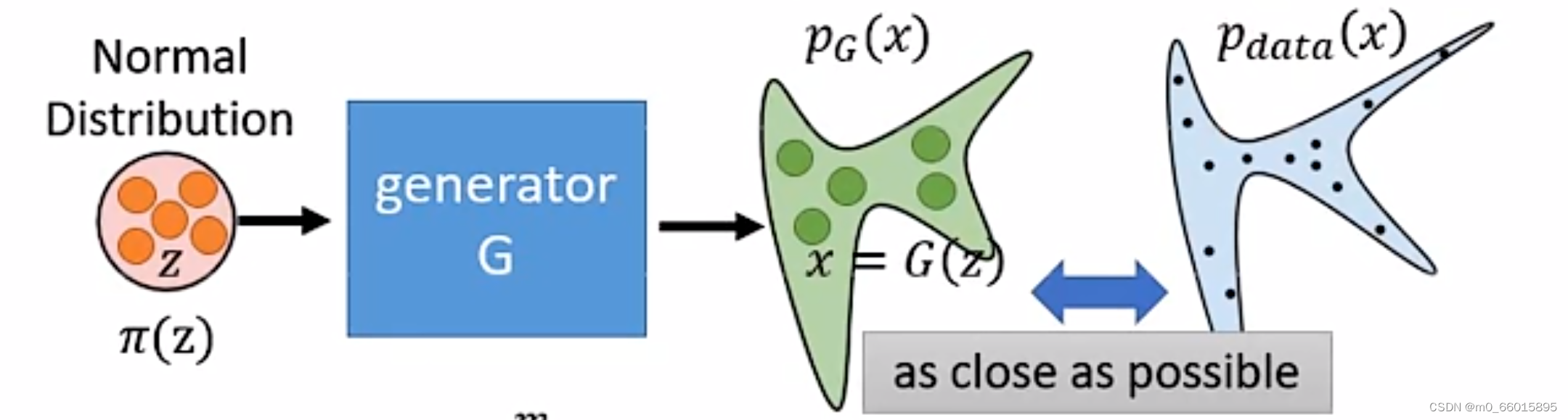
而我们训练生成器的目的就是希望这个和真实数据的分布
越接近越好,如下的极大似然函数求解即生成器G的求解,其中
是从
分布中采样得到的,因此极大似然的结果就是每个样本被采样得到的最大概率。
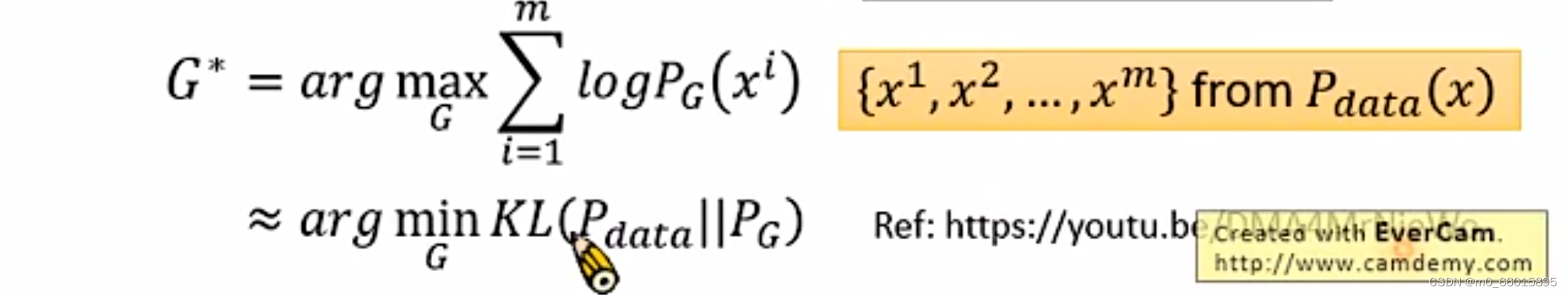
Math Background(数学背景)
Jacobian Matrix(雅可比矩阵)
已知,
是关于z的函数,那么
的雅可比矩阵就是下图的

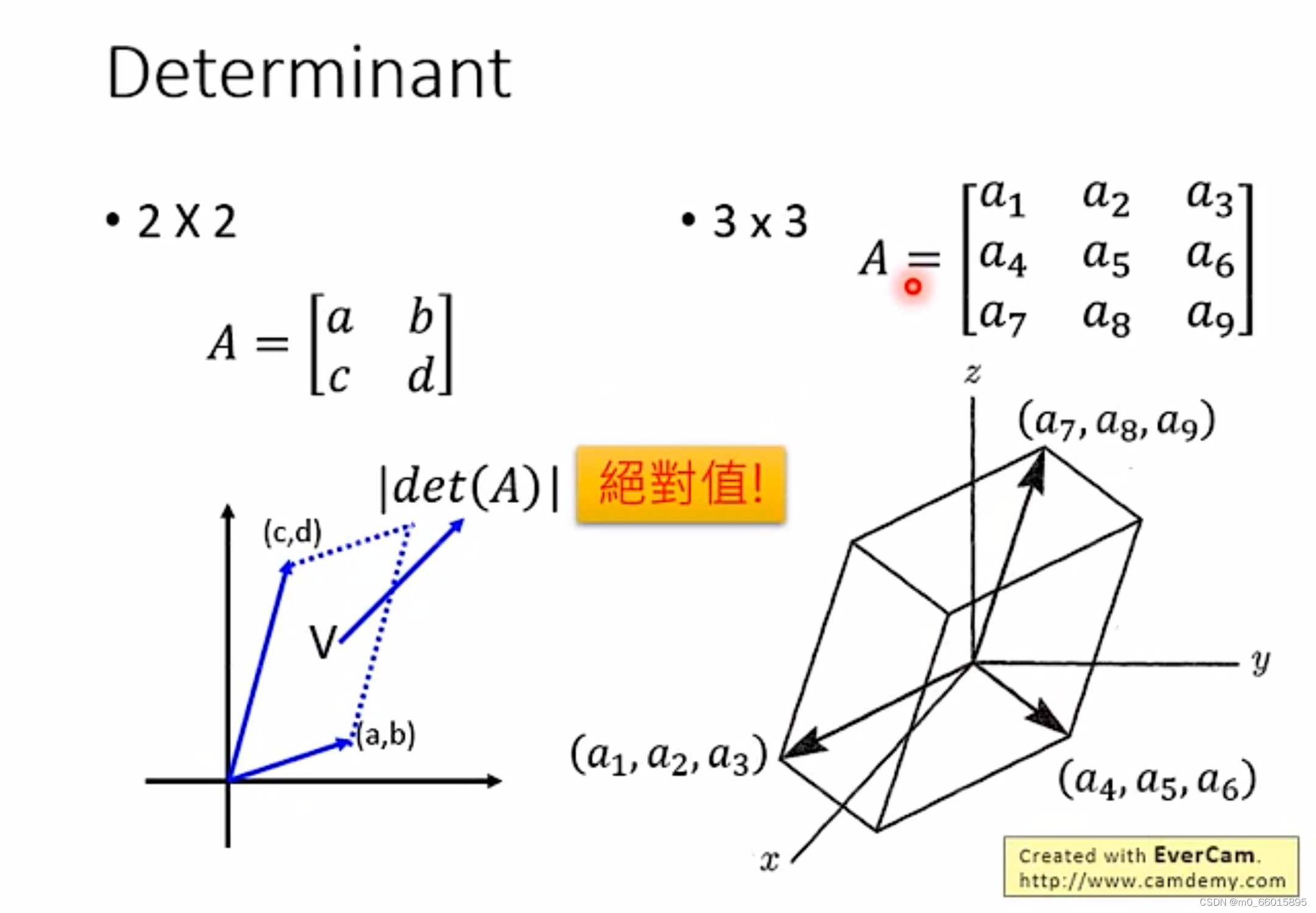
计算雅可比矩阵就需要用到行列式,行列式在空间维度上的含义,就是矩阵的每一行都可以当作一个向量,在对应维度的空间展开,例如二维行列式的绝对值在二维空间就是向量展开图形的面积,三维的则是体积。
Change of Variable Theorem(变量变化理论)
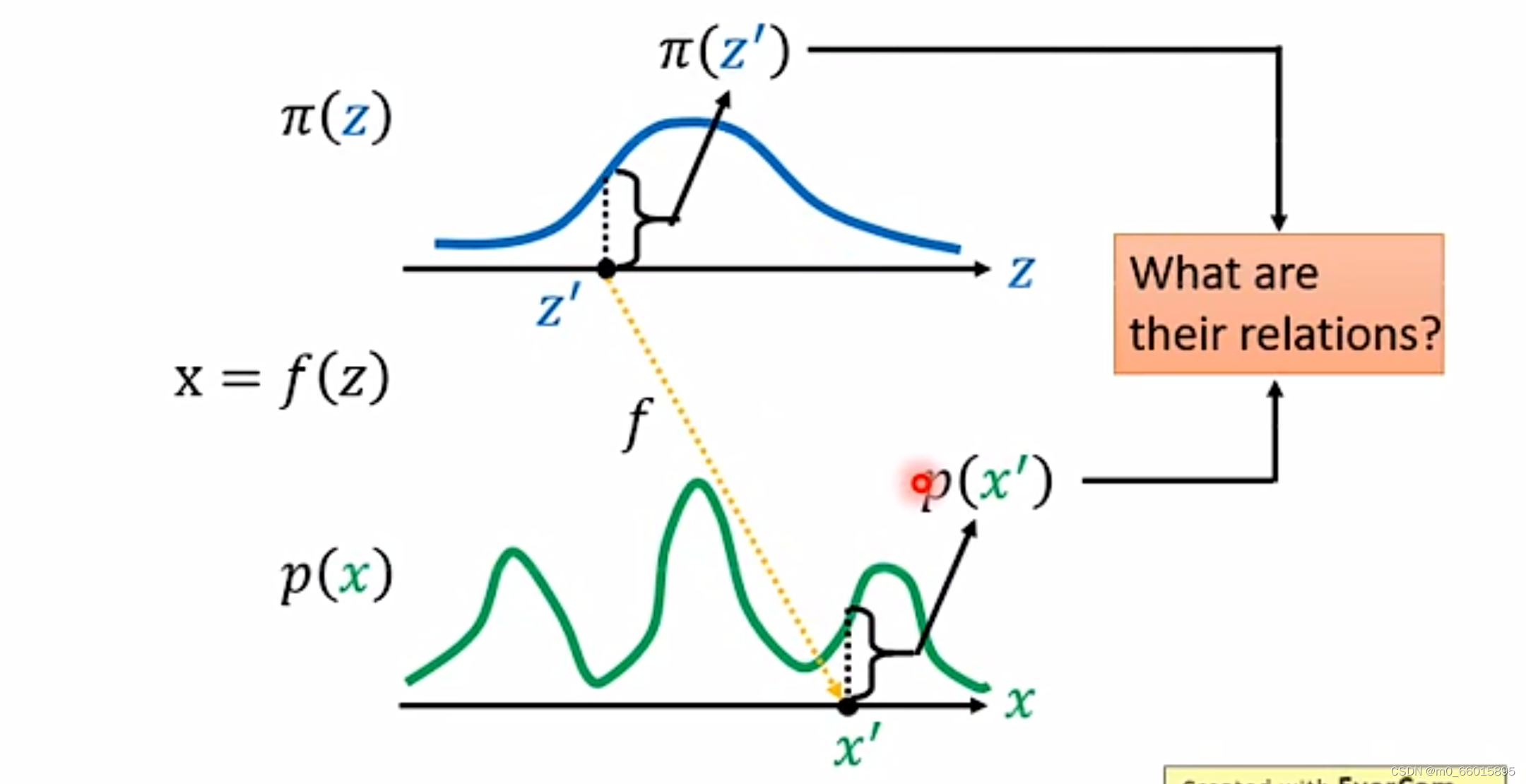
给定两组数据z和x,其中z服从现我们已知的简单先验分布(通常是高斯分布),x服从复杂分布
(即训练数据代表的分布)。而分布Z输入生成器得到的分布下,那生成器是怎么通过分布Z得到分布X的呢?如果在分布Z上取一点
,对应分布X上的
,那么
与
之间有什么关系呢?因此我们需要找到这个变换函数
,通过这个变换函数就实现了一个生成模型的构造。因为,p(x)中的每一个样本点都代表一张具体的图片,如果我们希望机器画出新图片的话,只需要从π(z)中随机采样一个点,然后通过f: z → x,得到新样本点 x,也就是对应的生成的具体图片。
先举一个简单的例子,假设 z 和 x 都是一维分布,其中 z 满足简单的均匀分布:,x 也满足简单均匀分布:
。因此可以得到x与z的关系用转换函数表示
。
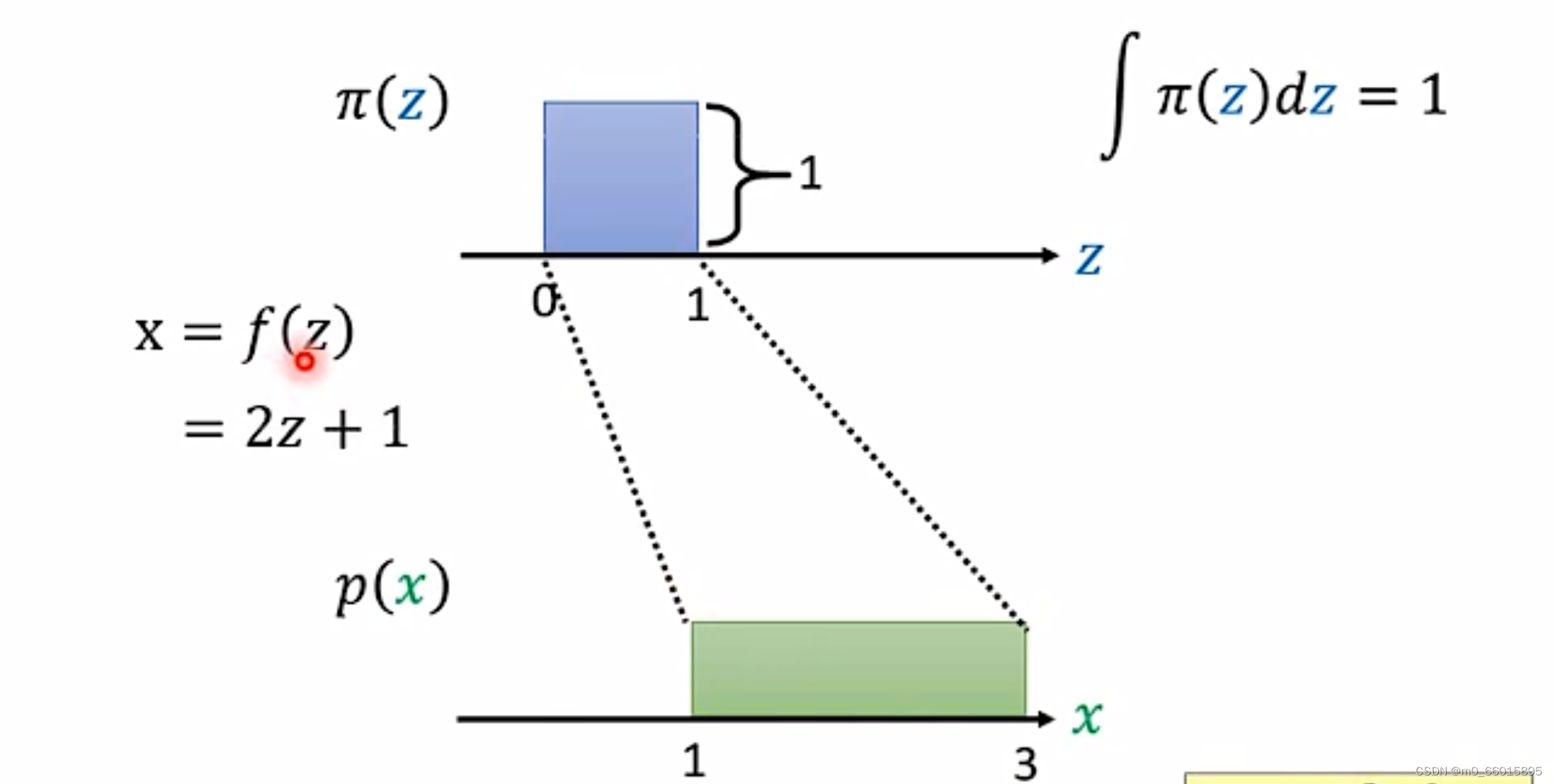
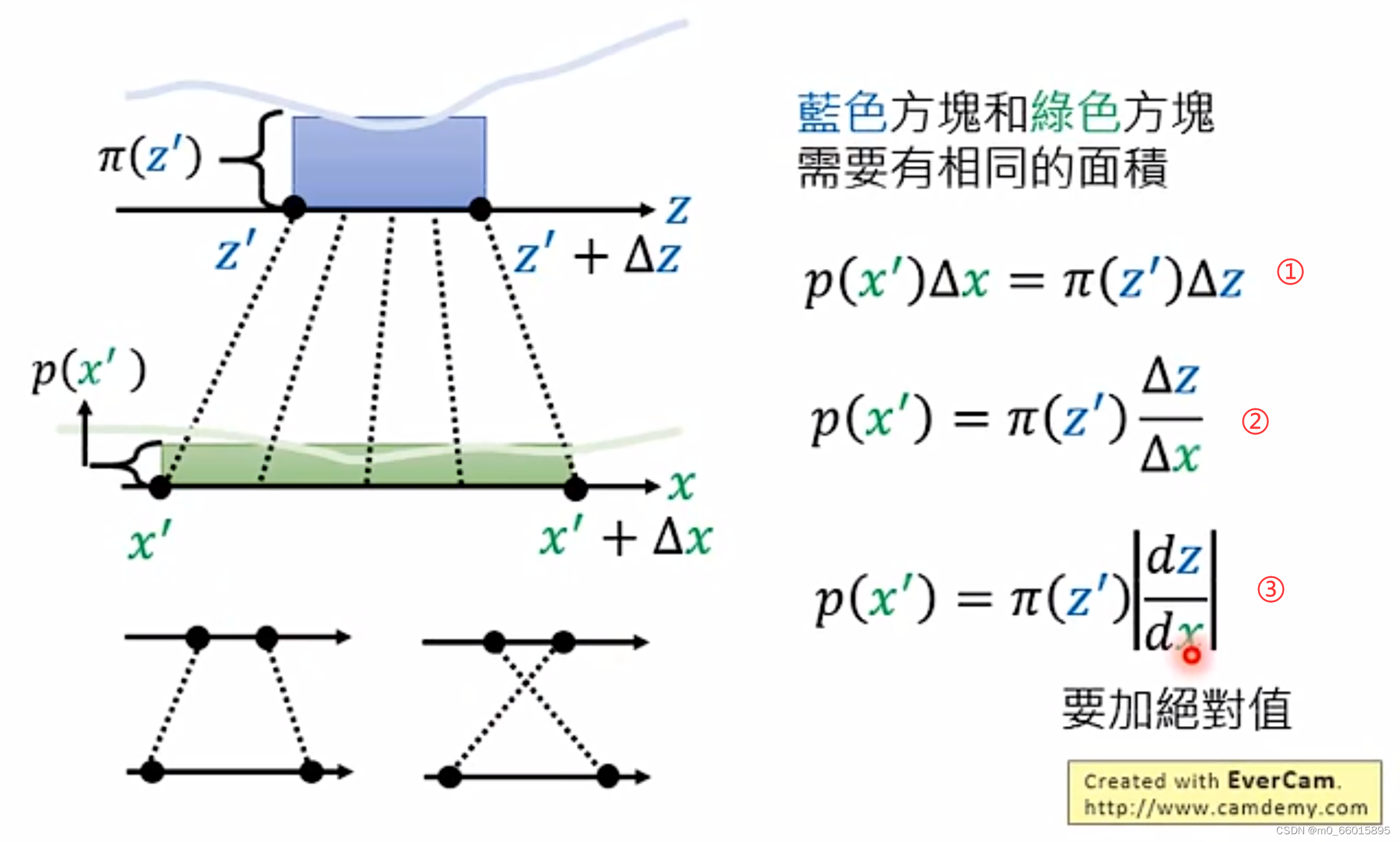
假设z和x的分布都为更加复杂的情况,如下图所示。在某点上取一定的增量
,那么对应映射到x的分布上,就也有
对应
,
对应到
。这两部分的面积相同,面积都为长×宽,因此可以得到下面的公式①,当增量足够小,这可以写成公式③微分的形式。
微分有正有负,z增加x也增加则微分为正,但当z增加x减少,或者x增加z减少,则微分为负。因此微分需要加上绝对值,
上面的例子是一维的,那如果扩展到二维空间,z和x都是二维的向量。假设当前的 处对于两个方向都进行了增量,那么映射到x之中将会有四个增量,蓝色的方形通过一个function变成绿色的菱形。
是
改变的时候
的改变量,
是
改变的时候
的改变量,
是
改变的时候
的改变量,
是
改变的时候
的改变量。
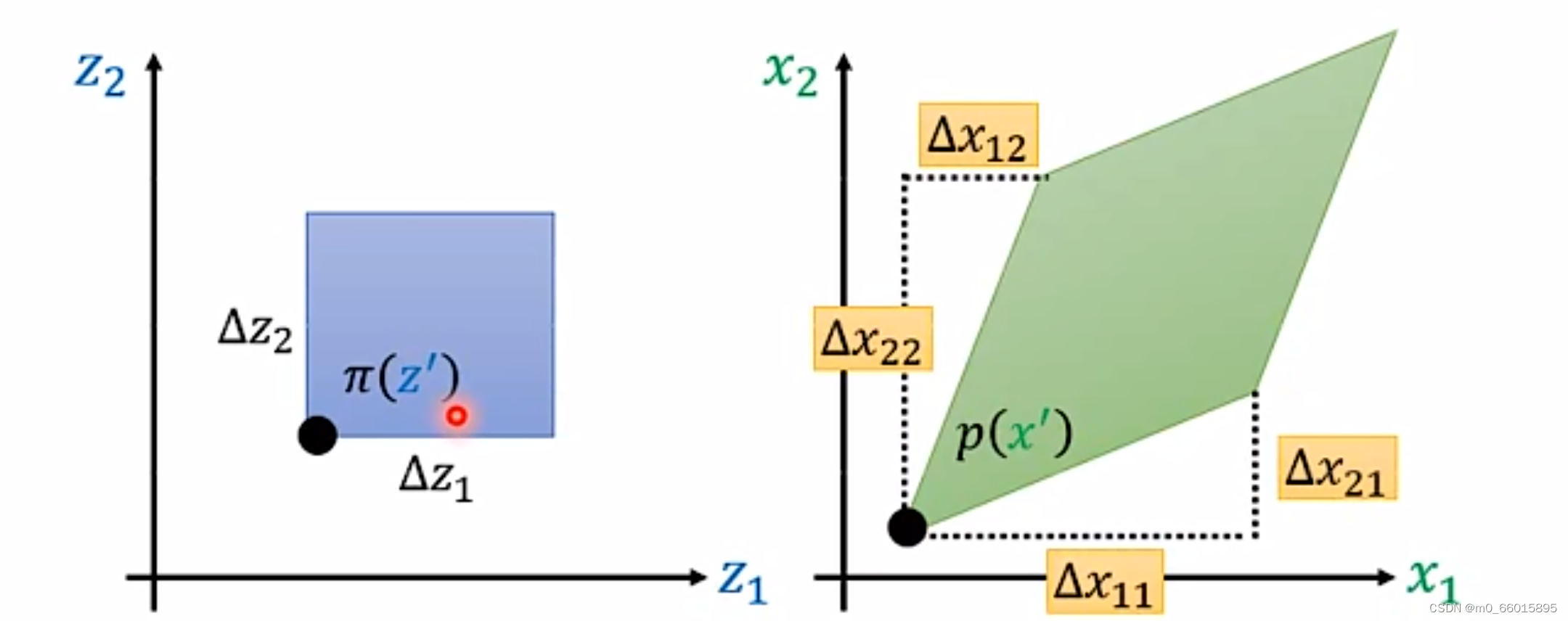
在一维空间他们之间的关系是面积相等,那么在二维空间他们的关系就是体积相等,其中和
代表高。由体积相等可以得到以下公式 :
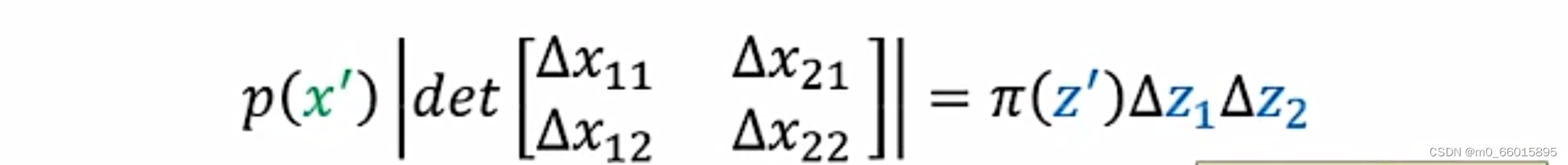
对这个公式进一步推导
- ①-->②:将
放入行列式里面,由行列式的定义,把det的第一行除以
,第二行除以
- ②-->③:
意思是当
改变的时候
的该变量,因此
就等于
对
的偏微分,同理可得其他三项。
- ③-->④:由
可知,把一个矩阵做对角的交换即b和c的位置进行交互,是不会改变行列式的值,因此将左下角与右上角做交换。
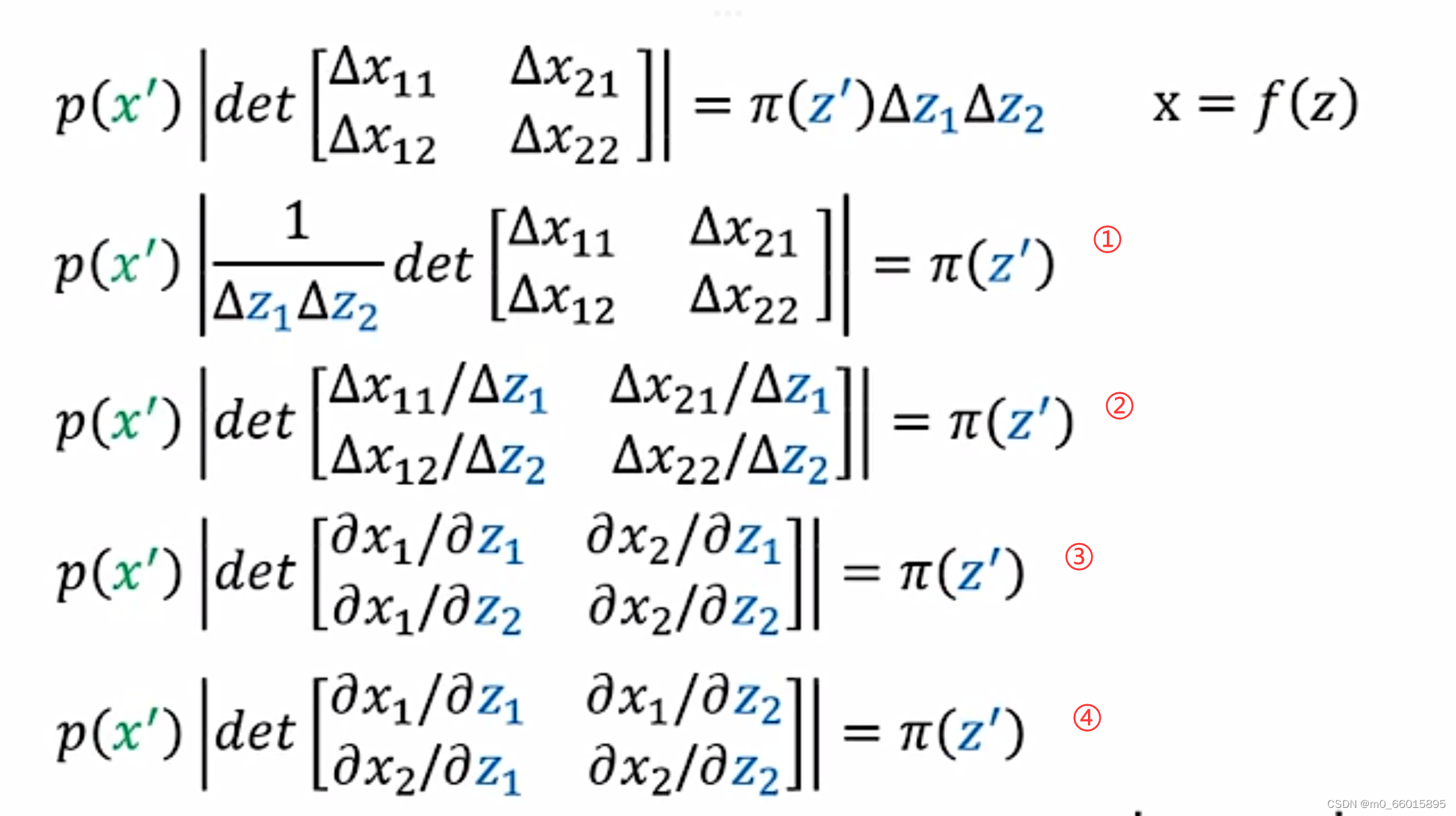
通过上图一系列行列式的变换,可以得到下图黄色框内的等式,因此我们得出结论:已知,则
和
两者之间的关系可以雅克比矩阵的行列式的绝对值相互映射
。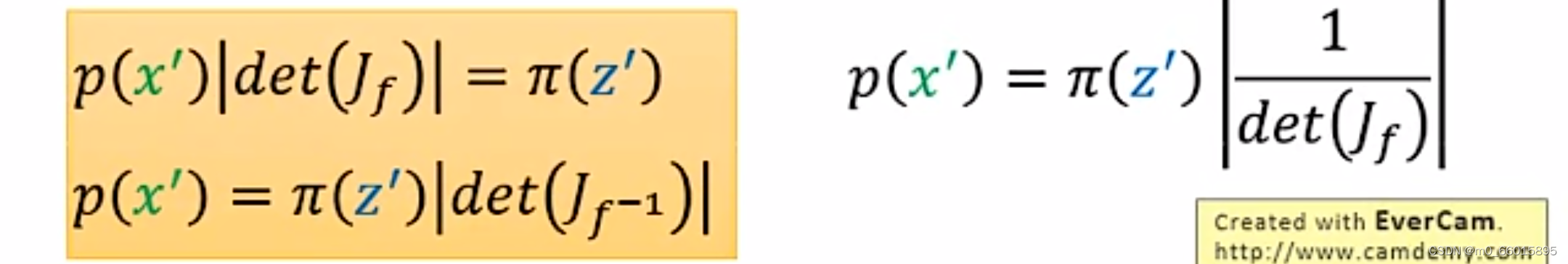
Flow-based Model(流模型)
经过上面数学背景的推导之后,可以将生成器目标函数进行如下转换:
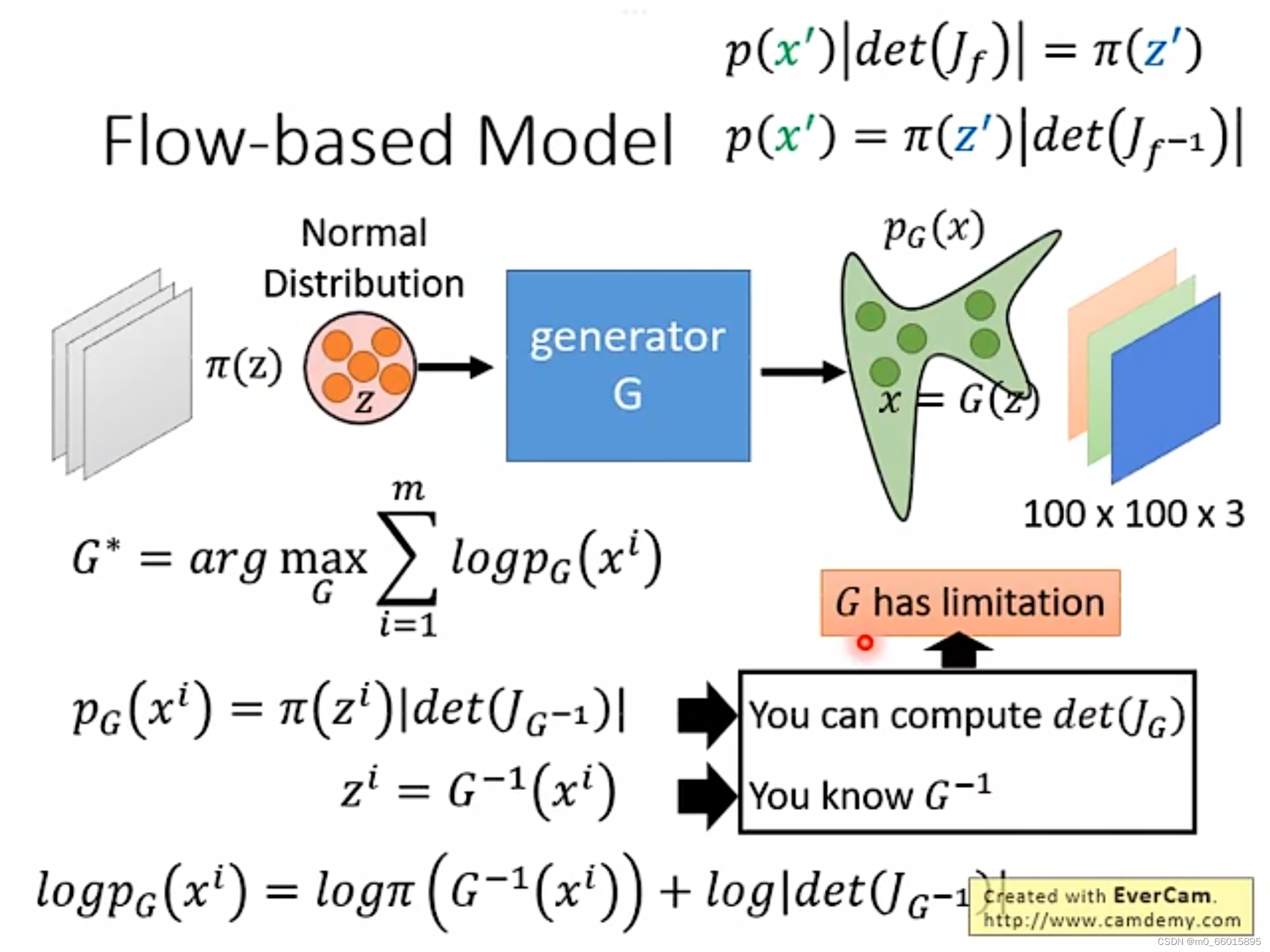
因此,要求目标函数的最大值,也就是求两项的最大值,首先需要知道怎么算雅克比矩阵的行列式,而的雅可比矩阵维度比较高,因此行列式的计算是一大困难;其次是要知道怎么算生成器G的逆
,也就是生成器通过输入得到输出,同时也可以将输出作为输入,因此要求输入的维度和输出的维度必须是一样的,这样才能保证生成器的可逆性。
由于我们的目标是求出G,但是又需要知道,所以我们要巧妙设计G的网络架构,而在实际的网络架构中,生成器G可能不止一个,因此叫作Flow-based Model,意味着像流水线一样。如果需要满足上述的各种条件,那就需要对G加上种种限制。那么单独一个加上各种限制就比较麻烦,我们可以将限制分散于多个G,再通过多个G的串联来实现,这也是称为流形的原因之一:
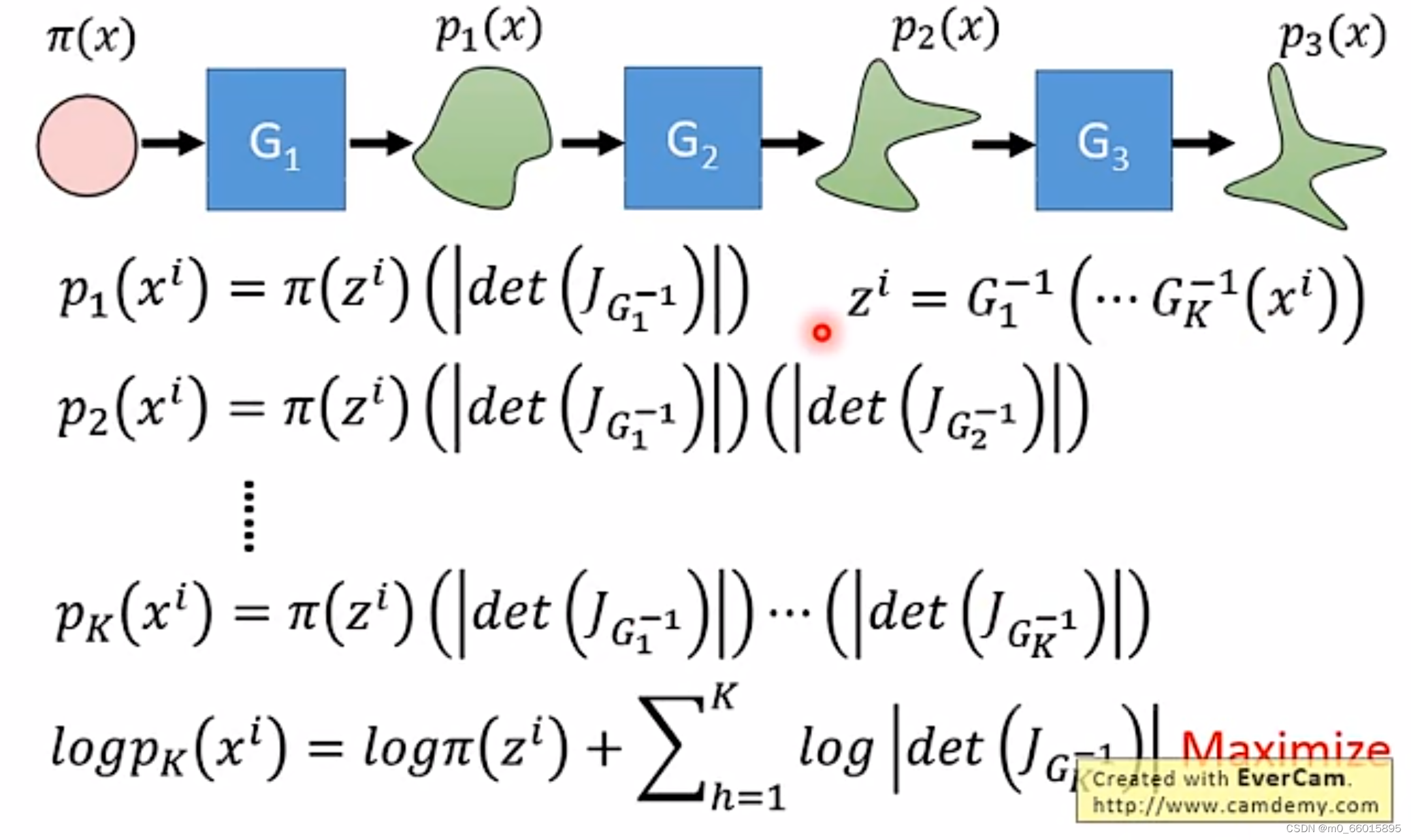
求目标函数生成器的最大值 ,要求的就是
的最大值,经过推导转换,
等于两项的和。我们在训练生成器的逆的时候就会从分布
中采样得到
,然后代入得到
,并且根据最大化
来调整
。那么如果只看等式右边的第一项,因为
是正态分布,因此当
即
取零向量的时候其会达到最大值。如果只看第一项的最大值的话,
全部取零向量,这时第一项将取到最大值,但是这会导致雅克比矩阵全为0(因为
都是零向量,因此没有变化的梯度),因此第二项的值将会无限接近负无穷。
由此可以看出这两项之间是相互约束的关系!所以z必须在两项之间平衡,才能得到最大值。这个平衡点就是我们的优化目标。
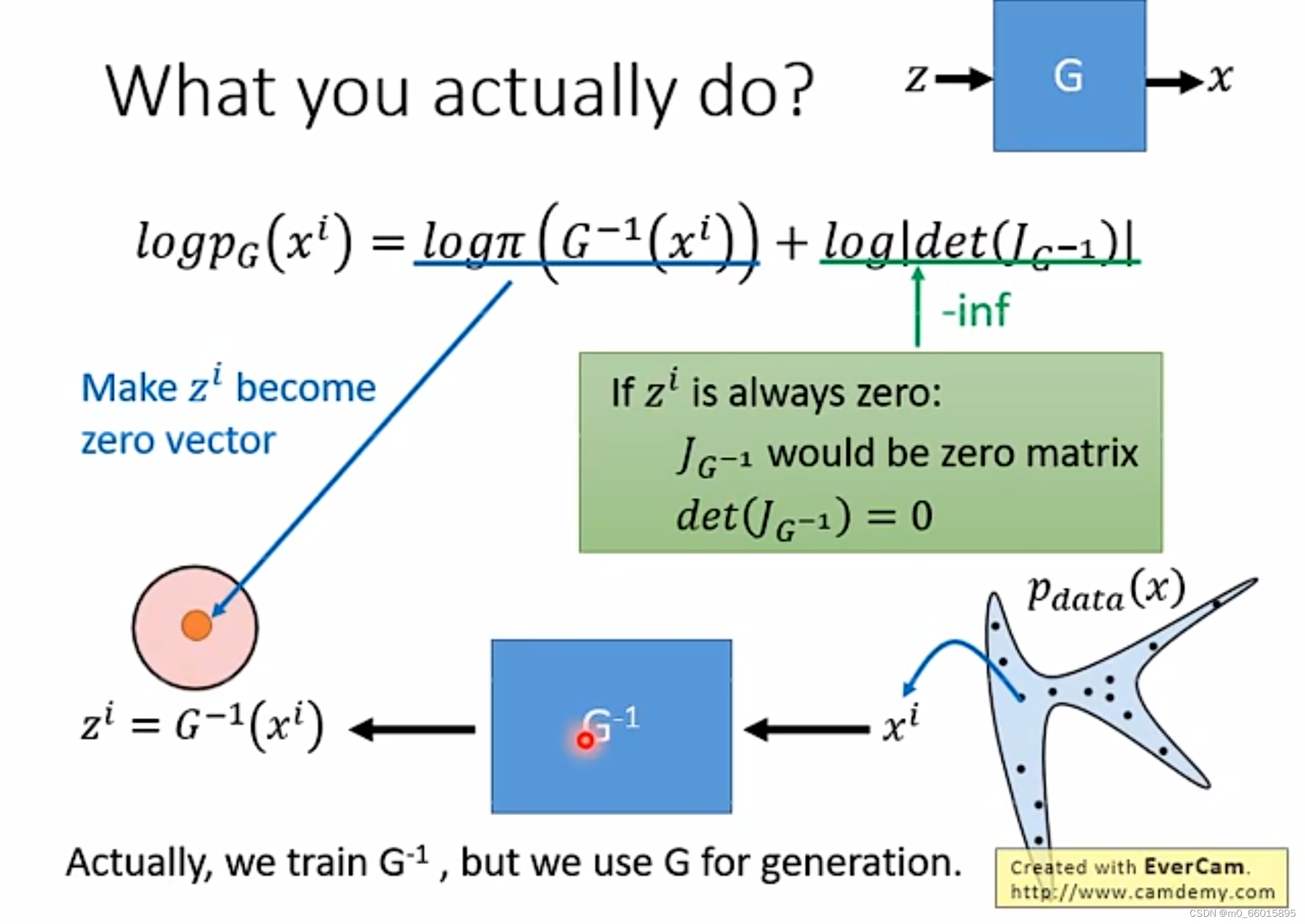
当可以计算出来的话,那么
的目标表达式只与
有关,所以在实际训练中,我们可以训练
对应的网络,然后想办法算出
,再用
来做图像生成。
Coupling Layer(耦合层)
计算雅可比矩阵方法
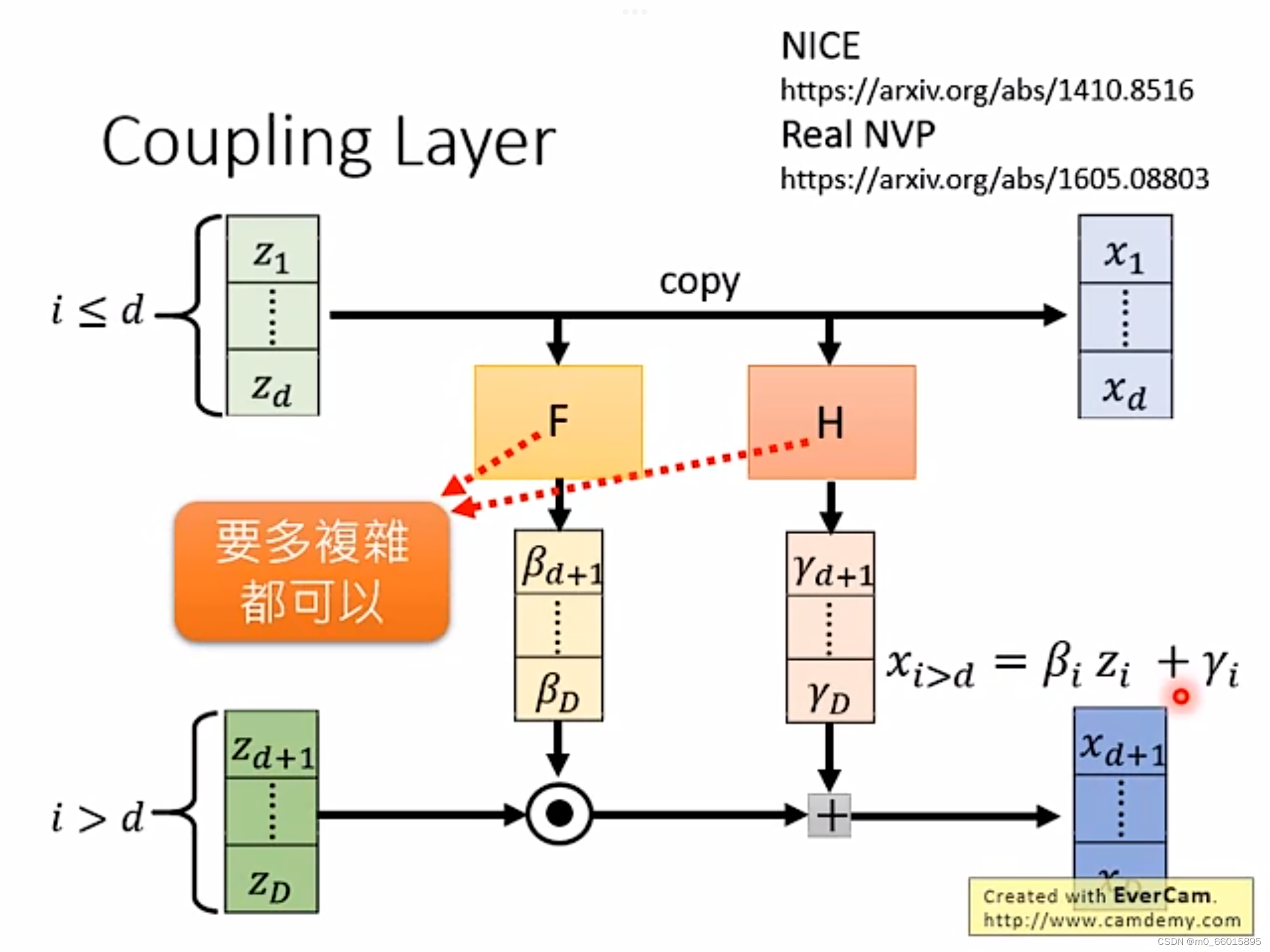
为了能够方便计算雅克比矩阵,NICE采用了一种称为耦合层(Coupling Layer)的设计,如下图所示:
将向量Z分为两份,而向量X的前d项可以直接由Z的前d项
复制得到,其中F和H是两个函数,由向量Z的前d项
乘以一个矩阵得到,而函数F和H两个函数是用来对向量进行变换,它可以很复杂。而
由
与函数F做点积再加上函数H得到。
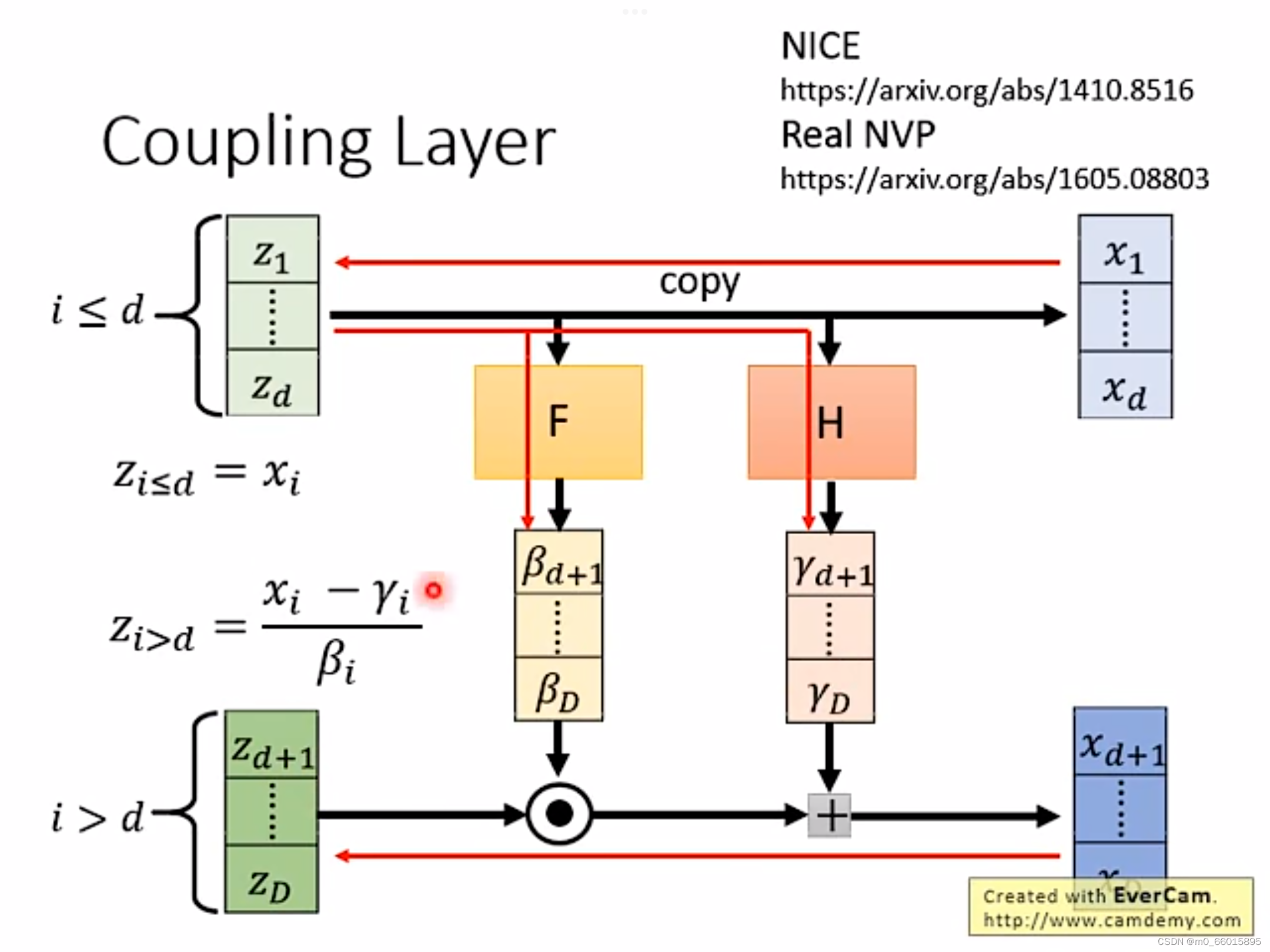
而上图是正向的过程,因为我们训练的时候是训练,因此我们需要负向的过程,如下图所示。反向的过程我们已知的是向量X,向量Z的前d项
由向量X的前d项
复制得到,而函数F和H不变,均由向量Z得到,而
由
减去
再除以
得到。
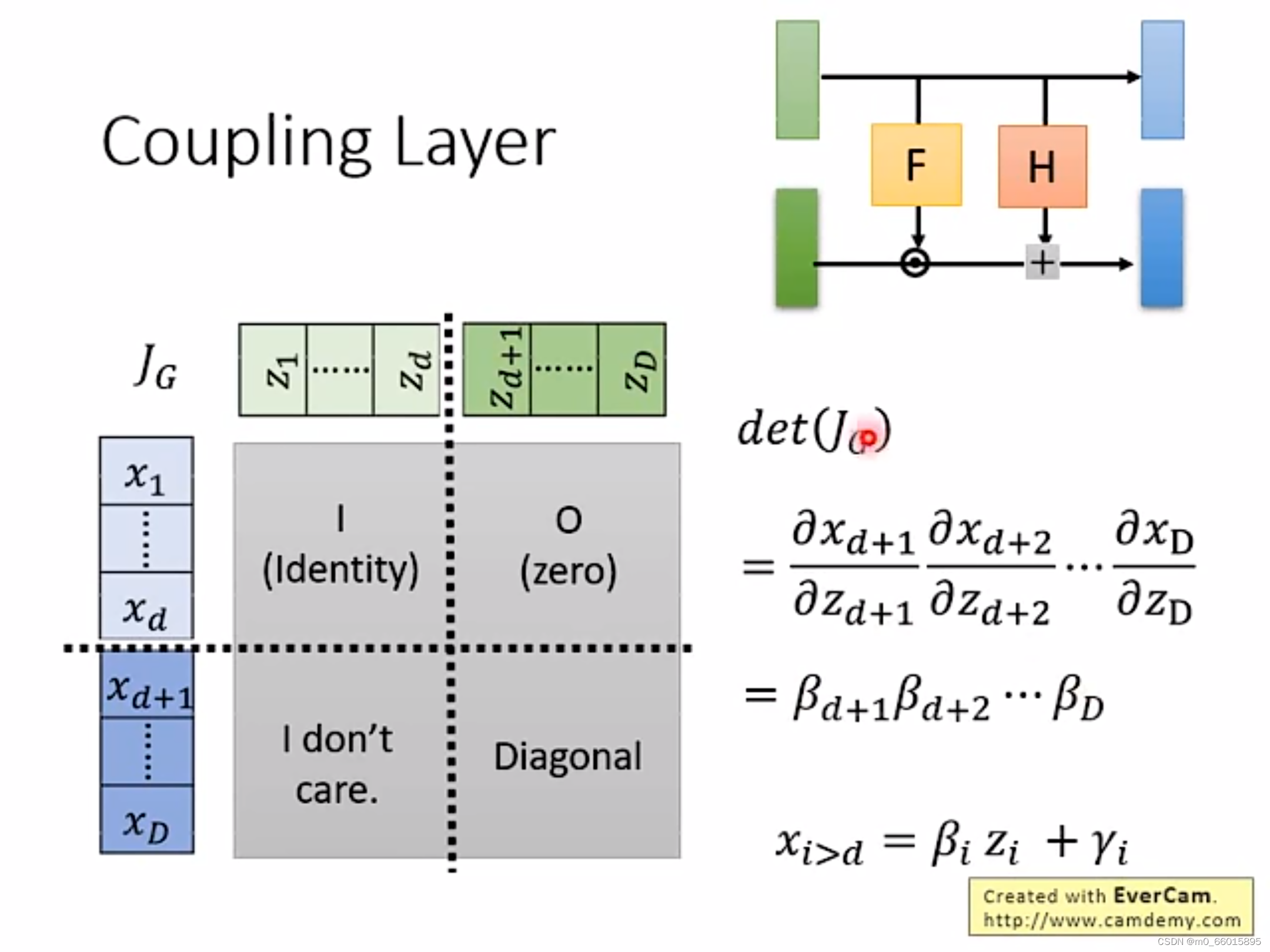
有了上面的关系之后,雅克比矩阵的计算就变得很方便了,由下图可以看出,左上角的矩阵为单位矩阵I,因为与是由复制得到,因此相等。右上角的矩阵为零矩阵,因为由复制得到与无关,因此没有任何关联,矩阵为0。左下角的矩阵不需要考虑,由线性代数的行列式计算可知,因为右上角的矩阵为零矩阵因此det的值与左下角的矩阵无关,右下角的矩阵为diagnosed,因为每个只与有关,因此为对角矩阵,因此det的值等于左上角矩阵乘以右下角矩阵,而左上角矩阵为单位矩阵,因此det的值等于右下角的对角矩阵的值,而对角矩阵的值等于对角线的值相乘,即
的值。
Stacking(叠加)
再接下来我们就可以将多个Coupling Layer串在一起形成一个完整的生成器,但如果正向直接串的话就会发现前d维度的值是直接拷贝的,这样会有一个新问题,就是最终生成数据的前d维与初始数据的前d维是一致的,这会导致生成数据中总有一片区域看起来像是固定的图样(实际上它代表着来自初始高斯噪音的一个部分)。如果需要解决这个问题,可以第一个Coupling Layer复制前面,第二个Coupling Layer复制后面,copy与affine模块进行位置上的互换交替使用,这样最终的生成图像就不会包含完全copy自初始图像的部分。
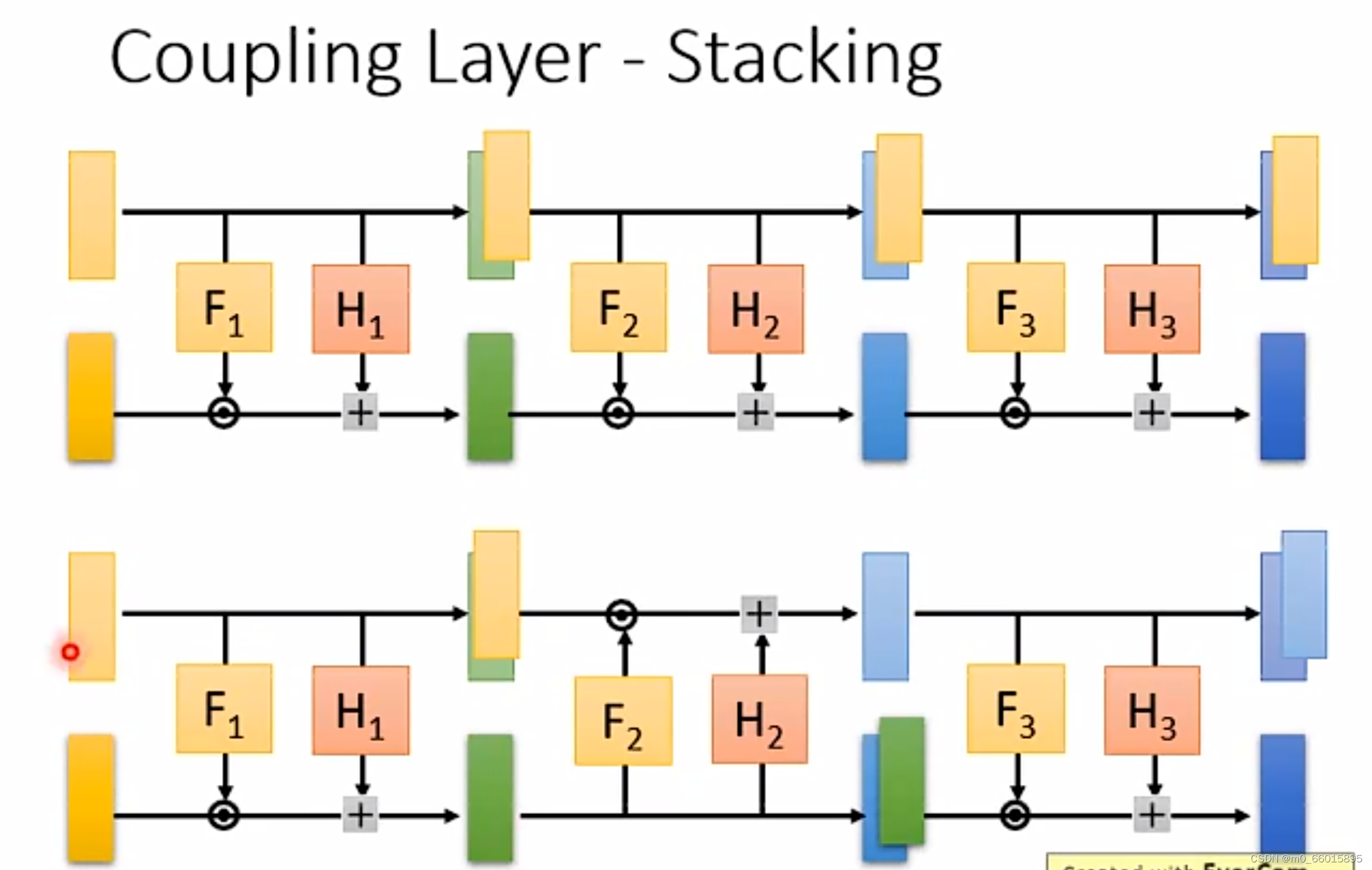
交替方法
在做影像生成的时候,怎么把一张image拆成两半做copy与affine模块互换?
第一个例子
下图展示了两种按照不同的数据划分方式做copy与affine的交替变换。左图代表的是在像素维度上做划分,即将横纵坐标之和为偶数的划分为一类,和为奇数的划分为另外一类,然后两类分别交替做copy和affine变换(两两交替);右图代表的是在通道维度上做划分,通常图像会有三通道,那么在每一次耦合变换中按顺序选择一个通道做copy,其他通道做affine(三个轮换交替),从而最终变换出我们需要的生成图形出来。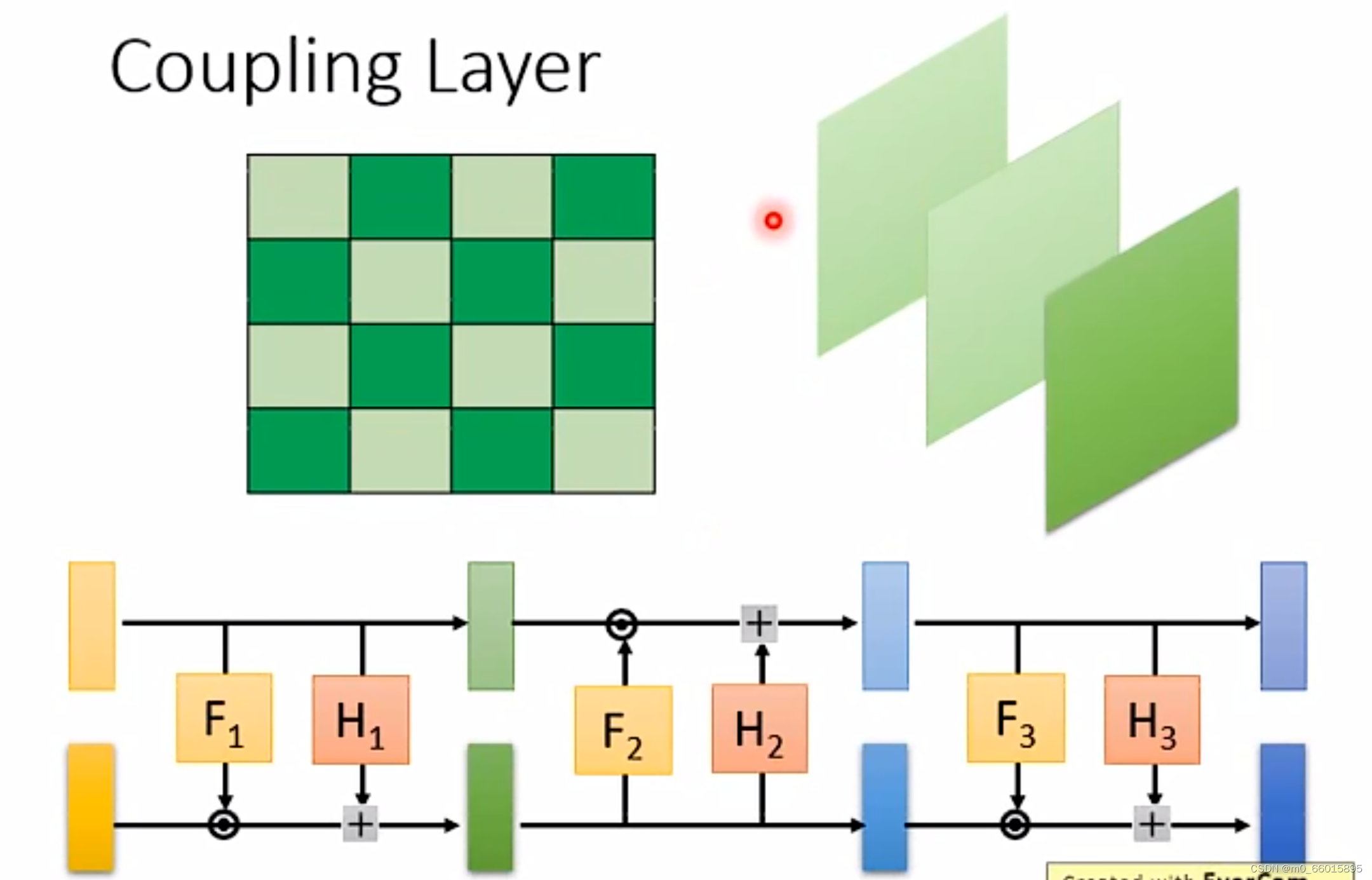
第二个例子:1✖1的卷积
这一个方法在GLOW模型中提出,如何进行copy和affine的变换能够让生成模型学习地更好,这是一个可以由机器来学习的部分,所以我们引入W矩阵,帮我们决定按什么样的顺序做copy和affine变换,这种方法叫做1×1 convolution。1×1 convolution只需要让机器决定在每次仿射计算前对图片哪些区域实行像素对调,而保持copy和affine模块的顺序不变,这实际上和对调copy和affine模块顺序产生的效果是一致的。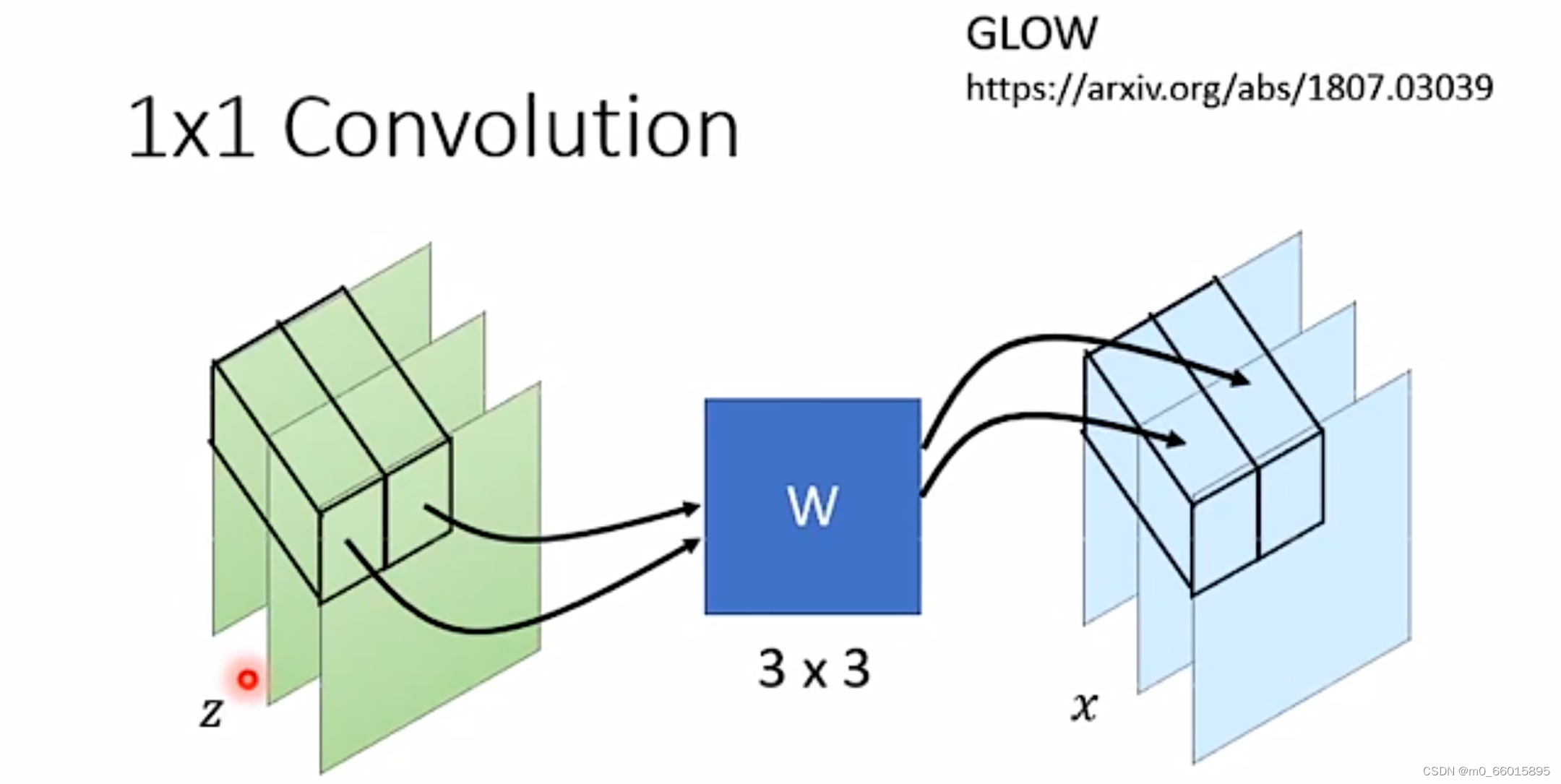
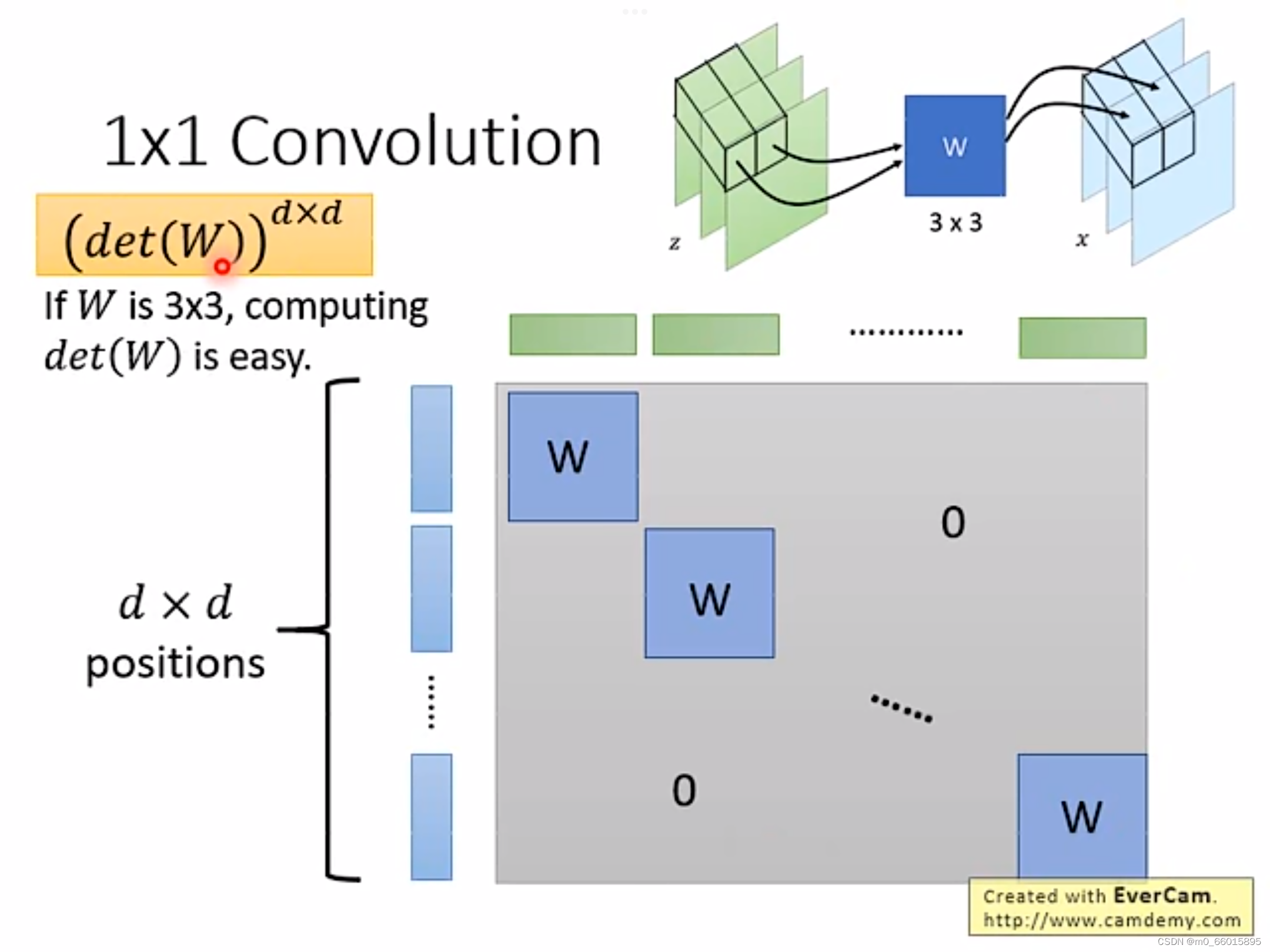
每个piexl 都乘以W得到x,因此Z和X的关系矩阵中,只有对应到同样的位置的蓝色和绿色向量是有关系的,因此只有对角线有值也就是W,因此这个Jacobian Matrix的值等于,如果W是一个3✖3的矩阵,那么det(W)的值就很容易计算。
手推change of variables therem

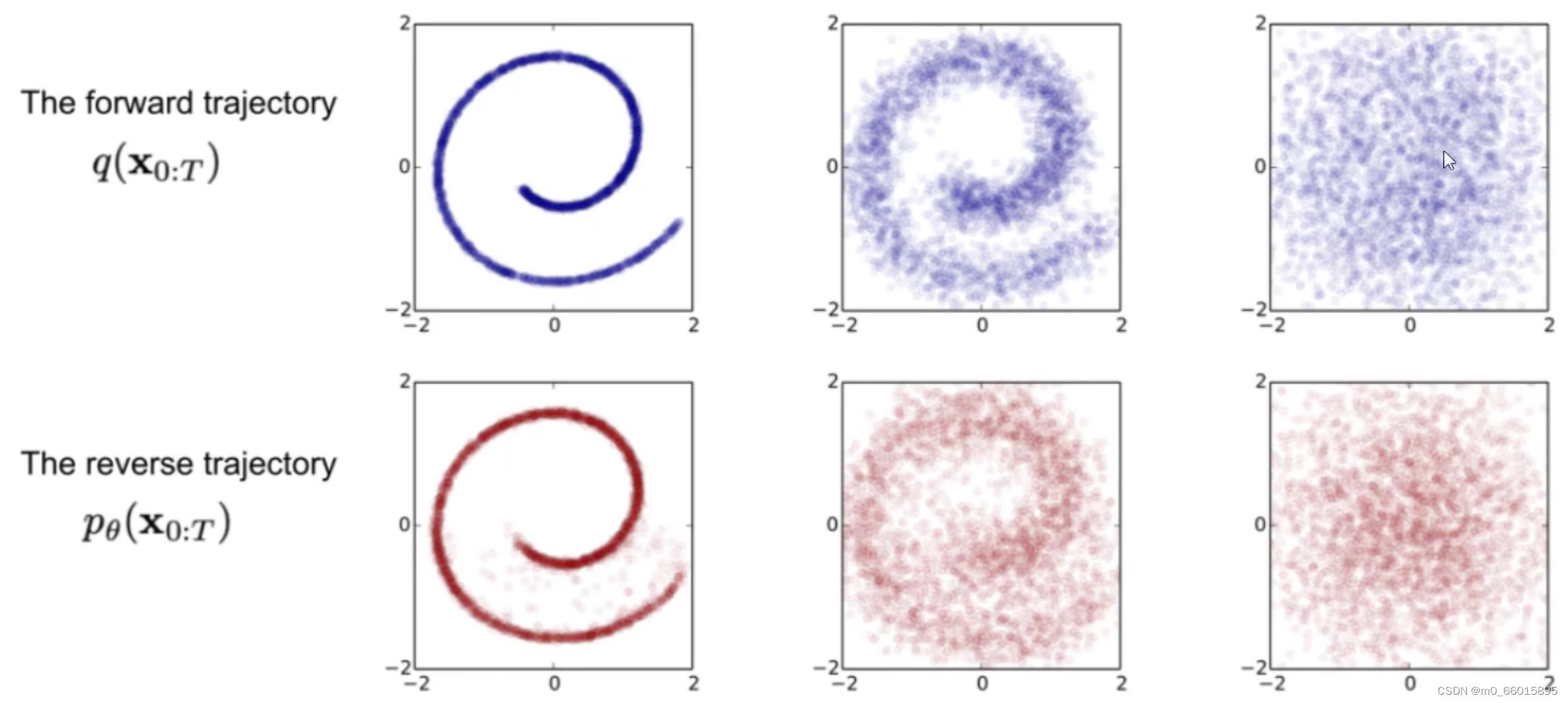
Diffusion Model(扩散模型)
Diffusion Model (扩散模型) 是一类生成模型, 和 VAE 、GAN等生成网络不同的是, 扩散模型在前向阶段对图像逐步施加噪声, 直至图像被破坏变成完全的高斯噪声, 然后在逆向阶段学习从高斯噪声还原为原始图像的过程,大致分为3步:
1.前向过程(加噪)
不断往最初输入数据中增加噪声,每一个时刻都要增加高斯噪声,后一时刻都是前一时刻增加噪声得到,这个过程可以看做不断构建标签的过程,最后变成纯噪音。

2.反向过程(去噪)
从一个随机噪声开始,逐步还原成不带噪音的原始图片即去噪过程,逆向过程其实时生成数据的过程。

3、 从噪声中生成随机图像
模型训练完成后, 只要给定高斯随机噪声, 就可以生成一张从未见过的图像。
VAE、GAN、Flow和Diffusion的对比
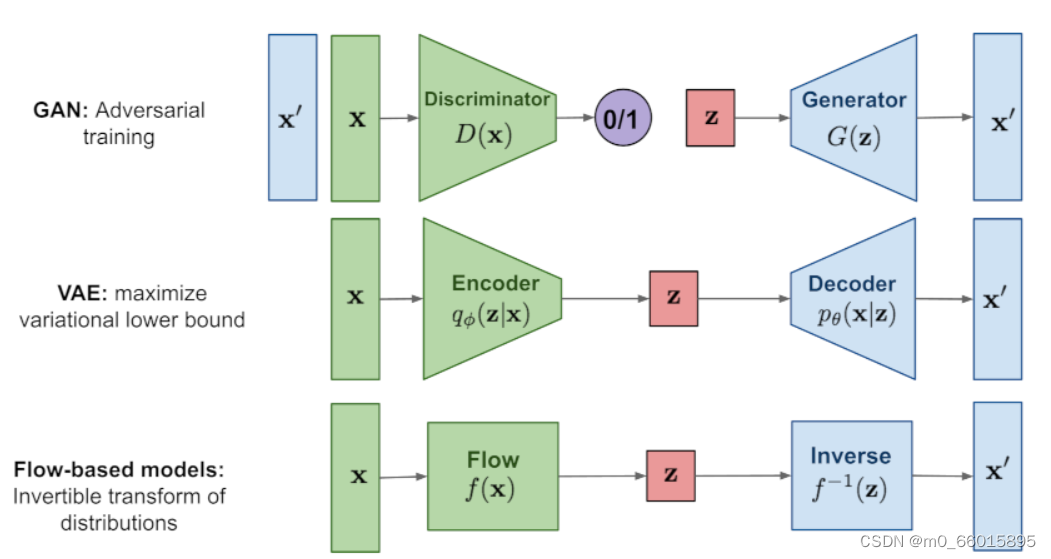
现在我们通过一个比喻来说明它们之间的区别。我们把数据的生成过程,也就是从Z映射到X的过程,比喻为过河。河的左岸是Z,右岸是X,过河就是乘船从左岸码头到达右岸码头。船可以理解为生成模型,码头的位置可以理解为样本点Z或者X在分布空间的位置。不同的生成模型有不同的过河的方法,如下图所示:
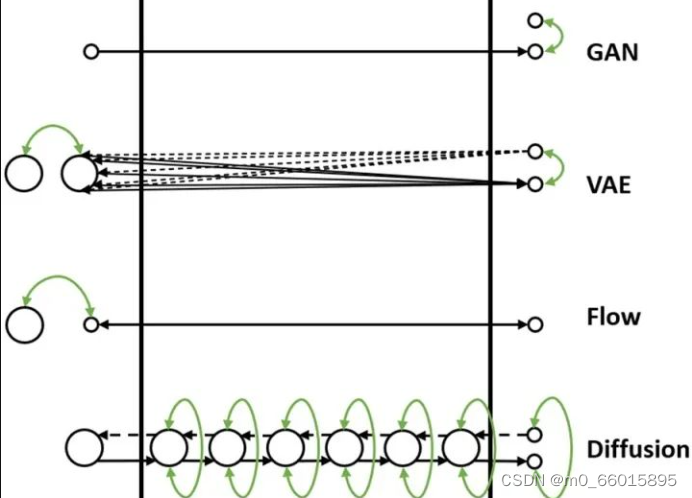
1. GAN的过河方式
随机生成一个简单分布z,直接通过对抗损失的方式强制引导船开到右岸,要求右岸下船的码头和真实数据点在分布层面上比较接近。
2. VAE的过河方式
VAE在过河的时候,会先考虑如果右岸的数据运到左岸,到达河左岸会落在什么样的码头。因为VAE编码器的输出是一个高斯分布的均值和方差,所以一个右岸的样本数据X到达河左岸的码头位置不是一个固定点,而是一个高斯分布,这个高斯分布在训练时会和一个先验分布(一般是标准高斯分布)接近。如果知道右岸数据到达左岸大概落在哪些码头,我们直接从这些码头出发就可以顺利回到右岸了。
3. Flow的过河方式
Flow的过河方式和VAE有点类似,也是先看看河右岸数据到河左岸能落在哪些码头,在生成数据的时候从这些码头出发,就比较容易能到达河右岸。
和VAE不同的是,对于一个从河右岸码头出发的数据,通过Flow到达河左岸的码头是一个固定的位置,并不是一个分布。而且往返的船开着双程航线,从右岸码头到达左岸码头经过什么路线,那么从左码头到右码头走的是同一条路线,这条航道是完全可逆的。因此Flow需要约束数据到达河左岸码头的位置服从一个先验分布(一般是标准高斯分布),这样在数据生成的时候方便从先验分布里采样码头的位置,能比较好的到达河右岸。
4. Diffusion的过河方式
Diffusion也借鉴了类似VAE和Flow的过河思想,要想到达河右岸,先看看数据从河右岸去到左岸会在哪个码头下船,然后就从这个码头上船,准能到达河右岸的码头。
但是和Flow以及VAE不同的是,Diffusion不只看从右岸过来的时候在哪个码头下船,还看在河中央经过了哪些桥墩或者浮标点。这样从河左岸到河右岸的时候,也要一步一步打卡之前来时经过的这些浮标点,能更好约束往返的航线,确保到达河右岸的码头位置符合真实数据分布。
Diffusion从河右岸过来的航线不是可学习的,而是人工设计的,能保证到达河左岸的码头位置,虽然有些随机性,但是符合一个先验分布(一般是高斯分布),这样方便我们在生成数据的时候选择左岸出发的码头位置。
因为训练模型的时候要求我们一步步打卡来时经过的浮标,在生成数据的时候,基本上也能遵守这些潜在的浮标位置,一步步打卡到达右岸码头。
如果觉得开到河右岸一步步这样打卡浮标有点繁琐,影响船的行进速度,可以选择一次打卡跨好几个浮标,就能加速船行速度,这就对应diffusion的加速采样过程。
总结
Flow-based Model通过雅可比行列式的变化,将目标函数进行转换,将目标从求生成器G转换为计算生成器的逆,在可以计算出G的逆的前提下得到的G再用来做生成。它通过巧妙地构造仿射变换的方式实现不同分布间的拟合,最终可以通过堆叠多个这样的耦合层去拟合更复杂的分布变化,从而达到生成模型需要的效果。下周将学习自监督机器学习。
参考




















 4791
4791











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








