6.9、移动迷宫小游戏（升级版）

最新推荐文章于 2025-05-16 14:00:49 发布

融码一生

最新推荐文章于 2025-05-16 14:00:49 发布

阅读量770

点赞数 13

分类专栏：《数据结构 & 算法》文章标签：算法图论深度优先数据结构

本文链接：https://blog.csdn.net/m0_66491750/article/details/137776537

版权

《数据结构 & 算法》专栏收录该内容

109 篇文章

订阅专栏

本文介绍了如何将二维数组表示的迷宫转化为图，以便应用迪杰斯特拉算法和广度优先搜索求解最短路径。并通过回溯法找到所有可能的最短路径，详细展示了基于C语言的编程实现过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

《移动迷宫》小游戏中，使用回溯法帮助骑士在迷宫中找到了通往出口的一条通路。
《移动迷宫》升级版：迷宫只有两个门：一个入口、一个出口。一个骑士骑马从入口走进迷宫，迷宫中设置有很多墙壁，对前进方向造成障碍。现需要你从迷宫中找到一条最短的通路，将行走路线和行走的最短距离告知骑士。
寻找最短路径最直接的方法就是使用迪杰斯特拉算法和弗洛伊德算法。
两种算法面对的数据结构是图，但迷宫是在二维数组中进行存储的，所以如果使用前面两种算法，则需要首先将二维数组转化为图的存储形式。

1、二维数组转化成图

3*3 迷宫（S为入口，E为出口，#为墙壁，-为通路）：

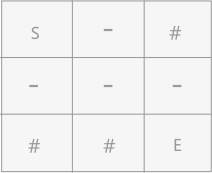
在编写程序向计算机中输入该迷宫的数据时，宜使用二维数组进行存储。但是无论是迪杰斯特拉算法还是弗洛伊德算法，其处理对象都是有向网或无向网。迷宫中并不涉及到具体的方向，所以需将存储迷宫的二维数组转化为无向网。
无向网的存储方式也是用二维数组来实现；将迷宫中所有的顶点看作是图中的顶点，因此上图的迷宫共有 9 个顶点，所以转化为无向网时需用 9*9 的二维数组表示。
在转化时，从迷宫的左上角（上图的 S 开始）一行一行的进行转化，对于每个顶点，只需判断其右侧和相邻的下方顶点是否为通路，如果是通路，转化为图中的直接体现就是两顶点之间有线连接。
例如，上图中的 S 右侧和下方的顶点都是-，骑士可以通过，在图中的表现就是 S 同其右侧顶点和下方顶点之间存储通路，如下图所示：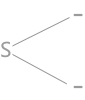
二维数组转化为图（每个顶点用其二维数组中的坐标来表示，00表示第 0 行第 0 列）：
二维数组转化为图的存储表示（1 表示有通路，0 表示没有通路；#表示墙壁，与其它任何顶点之间都没有通路）：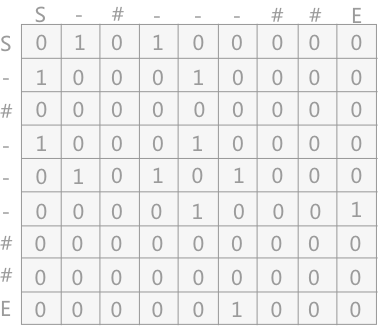

2、迪杰斯特拉算法：求迷宫的最短路径

#include <stdio.h>
#define MAX_VERtEX_NUM 200        // 顶点的最大个数
#define VRType int                // 表示弧的权值的类型
#define VertexType char           // 图中顶点的数据类型
#define INFINITY 65535

typedef enum{false,true} bool;

typedef struct {
    // 存储图中顶点数据
    VertexType vexs[MAX_VERtEX_NUM];    
    // 二维数组, 记录顶点之间的关系
    VRType arcs[MAX_VERtEX_NUM][MAX_VERtEX_NUM];   
    // 记录图的顶点数和弧（边）数
    int vexnum,arcnum;                      
}MGraph;

// 用于存储最短路径中经过的顶点的下标
typedef int PathMatrix[MAX_VERtEX_NUM]; 
// 用于存储各个最短路径的权值和
typedef int ShortPathTable[MAX_VERtEX_NUM]; 

// 迪杰斯特拉算法，v0 表示有向网中起始点所在数组中的下标
void ShortestPath_Dijkstra(MGraph G, int v0, PathMatrix *p, 
                           ShortPathTable *D){
    // 用于存储各顶点是否已经确定最短路径的数组
    int final[MAX_VERtEX_NUM];
    
    // 对各数组进行初始化
    for (int v=0; v<G.vexnum; v++) {
        final[v]=0;
        (*D)[v]=G.arcs[v0][v];
        (*p)[v]=0;
    }
    
    // 以起点为下标的顶点为起始点, 所以不用再判断
    (*D)[v0]=0;
    final[v0]=1;
    int k = 0;
    for (int i=0; i<G.vexnum; i++) {
        int min=INFINITY;
        // 选择到各顶点权值最小的顶点, 即为本次能确定最短路径的顶点
        for (int w=0; w<G.vexnum; w++) {
            if (!final[w]) {
                if ((*D)[w]<min) {
                    k=w;
                    min=(*D)[w];
                }
            }
        }
        // 设置该顶点的标志位为 1, 避免下次重复判断
        final[k]=1;
        // 对从起点到各顶点的权值进行更新
        for (int w=0; w<G.vexnum; w++) {
            if (!final[w]&&(min+G.arcs[k][w]<(*D)[w])) {
                (*D)[w]=min+G.arcs[k][w];
                // 记录各个最短路径上存在的顶点
                (*p)[w]=k;
            }
        }
    }
}

// 在将二维数组转化为图的过程中, 需要判断当前的点是否越界或者是否为通路
bool canUsed(int i,int j,int n,int m,char a[][110]){
    if (a[i][j]!='#' && i>=0 && i<n && j>=0 && j<m) {
        return true;
    }
    return false;
}

int main(){
    char a[110][110];
    int n,m;
    scanf("%d %d",&n,&m);
    getchar();
    MGraph G;
    G.vexnum=0;
    G.arcnum=0;
    // 记录入口在图的顶点数组中的位置下标
    int start =0;
    // 记录出口在图的顶点数组中的位置下标
    int exit=0;
    // 初始化记录图的边的二维数组, 假设各个边的长度为无穷大, 即两顶点之间没有边
    for (int i=0; i<n*m; i++) {
        for (int j=0; j<n*m; j++) {
            G.arcs[i][j]=INFINITY;
        }
    }
    // 输入二维数组, 同时记录入口和出口的位置
    for (int i=0; i<n; i++) {
        for (int j=0; j<m; j++) {
            scanf("%c",&a[i][j]);
            G.vexs[i*m+j]=a[i][j];
            G.vexnum++;
            if (a[i]
                [j]=='S') {
                start=i*m+j;
            }else if(a[i][j]=='E'){
                exit=i*m+j;
            }
        }
        // 作用是为了读取缓存区中的换行符(因为迷宫是一行一行输入到内存中的)
        getchar();
    }
    // 将二维数组转换为无向图, 在转换时, 从二维数组的左上角开始, 每次判断当前
    // 顶点的右侧和下侧是否为通路, 这样所有的通路就可以转换为无向图中的边
    for (int i=0; i<n; i++) {
        for (int j=0; j<m; j++) {
            // 首先判断当前点是否为通路
            if (canUsed(i, j, n, m, a)) {
                if (canUsed(i+1, j, n, m, a)) {
                    // 设定两顶点之间的边的权值为 1
                    G.arcs[i*m+j][(i+1)*m+j]=1;
                    G.arcs[(i+1)*m+j][i*m+j]=1;
                    G.arcnum++;
                }
                if (canUsed(i, j+1, n, m, a)) {
                    G.arcs[i*m+j][i*m+j+1]=1;
                    G.arcs[i*m+j+1][i*m+j]=1;
                    G.arcnum++;
                }
            }
        }
    }
    PathMatrix P;
    ShortPathTable D;
    // 进行迪杰斯特拉算法
    ShortestPath_Dijkstra(G, start, &P, &D);
    // 如果最终记录的权值和还是无穷大, 证明, 入口和出口之间没有通路
    if (D[exit]==INFINITY) {
        printf("-1");
    }else{
        printf("入口到出口的最短路径长度为:\n");
        printf("%d\n",D[exit]);
        printf("入口到出口的最短路径为(逆序):\n");
        printf("(%d,%d) ",exit/m,exit%m);
        while (P[exit]!=0) {
            printf("(%d,%d) ",P[exit]/m,P[exit]%m);
            exit=P[exit];
        }
        printf("(%d,%d)\n",start/m,start%m);
    }
    return 0;
}

运行结果：

/*
程序输入：
3 3
S-#
---
##E
程序输出：
入口到出口的最短路径长度为:
4
入口到出口的最短路径为(逆序):
(2,2) (1,2) (1,1) (0,1) (0,0)
*/

3、广度优先搜索解决最短路径问题

除了以上两种直接求最短路径的方法，还可以用广度优先搜索算法查找最短路径，该算法的实现直接在二维数组中完成，没必要转化为图的形式。
以上图中的迷宫为例，骑士一开始只能选择向右走，当走到坐标为 (2,2) 的位置时骑士有两个选择：向上走或向下走。
广度优先搜索的实现基于队列，在搜索的过程中将每种可选情况都入队，然后一轮一轮的对队列中的可选情况进行尝试，直到尝试出想要的结果为止。相当于骑士会分身术，一分为二，一个往上、一个往下，每个人每次只能走一步（你走一步然后我走一步）。
假设骑士走下、分身去上，当骑士走到坐标为（3，4）的位置时，又需要选择，要么往右、要么往下，此时骑士又分身、各走各的。但是无论怎么分，所有的骑士都是每次只走一步。
这种情况下，只要有一个骑士找到出口时，他所走的路径就绝对是最短路径。
广度优先搜索类似于在遍历一棵二叉树时一层一层地遍历（从上往下、从左往右），对于每种情况，轮流去试探、每次只走一步。
使用广度优先搜索查找最短路径时，只能求得最短路径的长度，如果想获取最短路径的具体路线，还需要结合其他算法。
存储迷宫时对每个顶点都分配一个整形变量，在进行广度优先搜索时，骑士和其分身每走一步，该顶点所携带的整形变量的值都是骑士之前所处位置的整形变量 +1。
例如，下图的迷宫中，骑士在最终找到出口时的整形变量为：
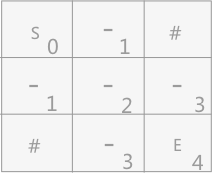
从入口开始，初始值假设为 0，其右侧通路和下方通路的整形变量的值是0+1=1，最终其出口自身所携带的整形变量值就是最短路径的长度。
通过对“骑士们”所走路线中整形变量的设置，此时可以结合回溯法，从入口开始寻找骑士所可能走的所有的最短路径（此时找到的可能不只有一条）。
使用回溯法时，从入口出发，每次同当前顶点周围查找比自身整形变量值大 1 的顶点，就是骑士所走的路线。如果找不到，回退再找，直到将所有的情况都试探完。
解决移动迷宫问题：广度优先搜索 + 回溯法（完整代码）：

#include <stdio.h>

typedef enum{false,true} bool;

typedef struct {
    int x;
    int y;
    char mess;
    int value;
}check;

bool canUsed(int x,int y,char data,int n,int m){
    if (x>=0 && x<n && y>=0 && y<m && data!='#') {
        return true;
    }
    return false;
}

void createMaze(int n, int m, check a[][110], int *entryx,
                int *entryy, int *exitx, int *exity){
    for (int i=0; i<n; i++) {
        for (int j=0; j<m; j++) {
            scanf("%c",&a[i][j].mess);
            a[i][j].x=i;
            a[i][j].y=j;
            if (a[i][j].mess=='S') {
                *entryx=i;
                *entryy=j;
            }else if(a[i][j].mess=='E'){
                *exitx=i;
                *exity=j;
            }
        }
        getchar();
    }
}

// 使用的广度优先搜索的思想, 采用队列的数据结构实现
void findRoad(check a[][110], int top, int rear, check queue[],
              int *value, int entryx, int entryy, int n, int m){
    // 首先将入口顶点入队
    check data;
    data.x=entryx;
    data.y=entryy;
    a[entryx][entryy].mess='#';
    data.mess=a[entryx][entryy].mess;
    data.value=0;
    queue[rear]=data;
    bool success=false;
    rear++;
    // 队列不满
    while (top!=rear) {
        // 逐个出队
        check temp=queue[top];
        a[temp.x][temp.y].value=temp.value;
        top++;
        // 对于出队的顶点判断是否是出口, 首个判断为出口的顶点, 其 value 值就是
        // 最短路径的长度
        if (temp.mess=='E') {
            *value=temp.value;
            printf("%d\n",temp.value);
            success=true;
            break;
        }
        // 每次入队, 判断其上、下、左、右的顶点是否符合条件, 若符合, 则入队, 同
        // 时对其 value 值赋值为前一个顶点 value+1, 为了避免重复判断此顶点, 对
        // 每个入队的顶点, 设定其字符为 ‘#’
        if(canUsed(temp.x-1,temp.y,a[temp.x-1][temp.y].mess,n,m)){
            data.x=temp.x-1;
            data.y=temp.y;
            data.mess=a[temp.x-1][temp.y].mess;
            data.value=temp.value+1;
            queue[rear]=data;
            a[temp.x-1][temp.y].mess='#';
            rear++;
        }
        // 右边
        if(canUsed(temp.x,temp.y+1,a[temp.x][temp.y+1].mess,n,m)){
            data.x=temp.x;
            data.y=temp.y+1;
            data.mess=a[temp.x][temp.y+1].mess;
            data.value=temp.value+1;
            queue[rear]=data;
            a[temp.x][temp.y+1].mess='#';
            rear++;
        }
        // 下边
        if(canUsed(temp.x+1,temp.y,a[temp.x+1][temp.y].mess,n,m)){
            data.x=temp.x+1;
            data.y=temp.y;
            data.mess=a[temp.x+1][temp.y].mess;
            data.value=temp.value+1;
            queue[rear]=data;
            a[temp.x+1][temp.y].mess='#';
            rear++;
        }
        // 左边
        if(canUsed(temp.x,temp.y-1,a[temp.x][temp.y-1].mess,n,m)){
            data.x=temp.x;
            data.y=temp.y-1;
            data.mess=a[temp.x][temp.y-1].mess;
            data.value=temp.value+1;
            queue[rear]=data;
            a[temp.x][temp.y-1].mess='#';
            rear++;
        }
    }
    // 如果不成功, 证明出口和入口之间没有通路
    if (success==false) {
        printf("-1\n");
    }
}

// 用于输出最短路径时回溯过程中的判断
bool judgeValue(int x,int y,int n,int m){
    if (x>=0 && x<n && y>=0 && y<m ){
        return true;
    }
    return false;
}

// 在输出时, 由于最短路径中从入口开始, 一直到出口, 所经过的顶点的 value 值逐
// 渐 +1, 所以采用回溯法查找所有可能的最短路径
void displayRoad(check a[][110], int entryx, int entryy, int n,
                 int m, int value){
    // 设置静态数组, 实现栈的作用
    static check stack[1000];
    // 栈的栈顶
    static int top=-1;
    // 对于每个当前的顶点, 首先需要判断其是否符合最基本的要求, 由于在前期二维数
    // 组中的通路都变成了 ‘#’, 这里采用另一个关键字, value 的值为主关键字进行搜索
    if (judgeValue(entryx, entryy, n, m)) {
        // 回溯思想的实现用的是递归, 所以需要设置一个出口, 出口就是当查找到顶点
        // 的 value 值为最短路径的顶点数时, 表明此时已经搜索在出口位置, 此时就
        // 可以依次输出栈内存储的各个经过的顶点的坐标
        if (a[entryx][entryy].value==value) {
            for (int i=0; i<top; i++) {
                printf("(%d,%d) ",stack[i].x,stack[i].y);
            }
            printf("\n");
            return;
        }
        // 从入口出发, 判断当前点的上、下、左、右位置上的顶点是否符合要求:
        // 1、该顶点的坐标没有超出范围;
        // 2、该顶点的 value 值是前一个顶点的 value 值 +1, 如果都符合, 说明
        //    之前判断最短路径时就途径此顶点, 将其入栈进行保存
        if (judgeValue(entryx+1, entryy, n, m) && 
            a[entryx+1][entryy].value==a[entryx][entryy].value+1) {
            top++;
            stack[top]=a[entryx+1][entryy];
            displayRoad(a, entryx+1, entryy, n, m,value);
            // 当运行至此, 又两种情况: 途径此顶点最终找到出口, 并将最终结果输出,
            // 此时应将该顶点弹栈; 该顶点的路径不是正确的, 应弹栈; 两种情况都应弹栈
            top--;
        }
        if (judgeValue(entryx-1, entryy, n, m) && 
            a[entryx-1][entryy].value==a[entryx][entryy].value+1) {
            top++;
            stack[top]=a[entryx-1][entryy];
            displayRoad(a, entryx-1, entryy, n, m,value);
            top--;
        }
        if (judgeValue(entryx, entryy+1, n, m) && 
            a[entryx][entryy+1].value==a[entryx][entryy].value+1) {
            top++;
            stack[top]=a[entryx][entryy+1];
            displayRoad(a, entryx, entryy+1, n, m,value);
            top--;
        }
        if (judgeValue(entryx, entryy-1, n, m) && 
            a[entryx][entryy-1].value==a[entryx][entryy].value+1) {
            top++;
            stack[top]=a[entryx][entryy-1];
            displayRoad(a, entryx, entryy-1, n, m,value);
            top--;
        }
    }
}

int main(int argc, const char * argv[]) {
    check a[110][110];
    check queue[1000];
    int top=0,rear=0;   
    int n,m;
    int entryx = 0,entryy=0,exitx=0,exity=0;
    scanf("%d %d",&n,&m);
    getchar();
    // 创建迷宫, 并找到入口和出口的位置坐标
    createMaze(n,m,a,&entryx,&entryy,&exitx,&exity);
    // 在迷宫中查找从入口到出口的最短路径, 若有, 输出最短路径的长度; 反之输出 -1
    int value;
    findRoad(a,top,rear,queue,&value,entryx,entryy,n,m);
    // 输出所有的最短路径
    displayRoad(a, entryx, entryy, n, m, value);
    return 0;
}

运行结果：

/*
输入部分：
3 3
S-#
---
#-E
程序输出部分：
4
(1,0) (1,1) (2,1)
(1,0) (1,1) (1,2)
(0,1) (1,1) (2,1)
(0,1) (1,1) (1,2)
*/

通过对通路进行整体的回溯，可以找到所有可能的结果，这个例子中，有四条长度相同的最短路径。