一、基本原理
Lasso的核心思想:稀疏性和正则化
1. 稀疏性
Lasso通过引入L1正则化(即系数绝对值之和),能够将一些不重要的特征的系数压缩为零。这种稀疏性使得Lasso不仅是一个回归模型,还是一个特征选择工具。它可以帮助我们在高维数据中筛选出最重要的变量,从而简化模型并提高解释性。
2. 正则化的作用
正则化的目的是防止过拟合。在普通最小二乘法中,如果特征之间存在多重共线性(即特征高度相关),或者特征数量远大于样本数量,模型可能会过度拟合
训练数据,导致在测试数据上的表现不佳。Lasso通过对系数施加惩罚,限制了模型的复杂度,从而提高了泛化能力。
举例说明:
假设你在研究某种癌症的发生机制,收集了100名患者的基因表达数据,每名患者有10,000个基因的表达水平作为特征。你的目标是根据这些基因表达数据预测患者是否患有癌症。
但是面临如下问题:
1.数据维度非常高(n=10,000),而样本量相对较少(m=100);
2.大多数基因可能与癌症无关,只有少数基因是关键因素。
可以使用Lasso回归,将大多数无关系数压缩到0,只保留关键特征。
与岭回归区别:
岭回归:保留所有特征,并压缩参数;
Lasso回归:只保留关键特征。
二、数学原理
Lasso的目标是最小化以下目标函数:
![]()
L1正则化与L2正则化(如岭回归)的关键区别在于其形状:
L2正则化:![]() ,是一个平滑的二次函数。
,是一个平滑的二次函数。
L1正则化:![]() ,是一个非光滑的绝对值函数。
,是一个非光滑的绝对值函数。
由于L1正则化在零点不可导,它会对系数施加更强的压缩作用,导致某些不重要的系数被直接压缩为零。这种特性使得Lasso具有稀疏性,能够自动进行特征选择。
由于L1正则化项的存在,目标函数不再是平滑的(因为绝对值函数在零点不可导)。因此,无法像普通最小二乘法那样直接求解解析解,而是需要使用数值优化方法。
Lasso的目标函数可以等价地写成带约束的形式:
![]()
其中 t 是一个超参数,用于限制系数的L1范数。这个约束形式直观地说明了Lasso如何通过限制系数的总大小来实现稀疏性。
Lasso通常使用坐标下降法(Coordinate Descent)进行优化。这种方法的思想是:每次固定其他系数不变,单独优化一个系数 。
假设我们优化第 j 个系数 ,目标函数可以写为:
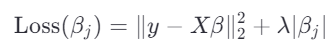
将 单独分离出来,目标函数可以改写为:
![]()
展开平方项:
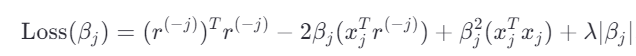
忽略与 无关的常数项
,目标函数简化为:
![]()
为了最小化上述目标函数,我们对分段分析,得到
的更新公式为:
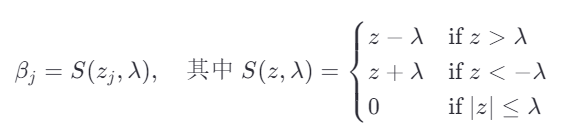
这就是著名的软阈值算子(Soft Thresholding Operator)。
基于上述推导,Lasso的优化算法可以通过以下步骤实现:
1.初始化所有系数 β=0;
2.对每个系数 :
计算残差=y-
;
计算=
。
使用软阈值算子更新:
=S(
,
)。
3.重复步骤2,直到收敛。
三、实例
# 导入必要的库
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
# 生成模拟数据
np.random.seed(42) # 设置随机种子以确保结果可重复
n_samples = 100 # 样本数
X = np.random.rand(n_samples, 4) * 10 # 随机生成4个特征
true_coefficients = np.array([3.5, -1.2, 0.8, 0]) # 真实系数
y = X @ true_coefficients + np.random.randn(n_samples) * 2 # 添加噪声的目标变量
# 将数据划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 构建Lasso模型
alpha = 0.1 # 正则化强度参数(对应公式中的λ)
lasso = Lasso(alpha=alpha)
# 训练模型
lasso.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = lasso.predict(X_test)
# 计算均方误差(MSE)
mse = mean_squared_error(y_test, y_pred)
print("测试集上的均方误差(MSE):", mse)
# 打印Lasso估计的系数
print("Lasso估计的系数:", lasso.coef_)
运行结果如下:
![]()




















 1834
1834

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








