一、 实验目的与要求
1.掌握高斯消元法求解线性方程组;
2.掌握Matlab编写代码,熟悉其画图工具,进行实验,并验证结果;
3.锻炼数学描述能力,提高报告的书写能力。
二、 问题

三、模型建立及求解
1、定理
根据线性代数知识,引入以下定理:
定理1:一n阶方阵A可逆的充分必要条件为
定理2:若一方阵可逆,则其逆矩阵唯一
定理3:将一个线性方程组的增广矩阵施行一系列初等行变换后得到的矩阵作为增广矩阵,其对应的线性方程组与原方程组同解
定理4:将行列式的任意倍加到另一行上,行列式的值不变
定理5:若一n阶方阵A是可逆的,则对于A和其逆矩阵有:
,其中
为n阶单位矩阵
2、高斯消元法求解
2.1高斯消元法思想
根据定理1可知,当,A是可逆的,对于线性方程组Ax=b,可写成
,又根据定理2,线性方程组有唯一解。在此不妨设
。
设矩阵A及其和向量b组成的增广矩阵分别为:
对进行初等行变换,由于
,所以矩阵每一列都至少有一个元素不为0。不妨假设
,定义行乘数:
。而后根据定理3,可进行初等行变换,使第i行减去第一行乘以
的值,即:
于是原增广矩阵变成:
当经n-1次上述变换,增广矩阵最终变成一个阶梯型矩阵:
记的余子式为
,按第一列展开计算
:
当,有
且
,而:
所以,
,以此类推
,于是有
,得到唯一解
,将
回代得到
唯一解,所以线性方程组有唯一解:
2.2高斯消元步骤
①构造增广矩阵:使用系数矩阵A和常数向量b构造增广矩阵
②初等行变换消元:定义行乘数,若行乘数存在,则通过一系列初等行变换,即:第i行—第k行×
,重复步骤将增广矩阵转化为阶梯形矩阵;若行乘数不存在,证明线性方程组不存在唯一解;
③回代求解:从最后一行开始,求出,将已求出值的未知数代入方程,求解出另一个未知数,然后根据:
依次向上回代,求解出其他未知数。
2.3算法复杂的分析
第k步消元时乘法运算次数为:,除法次数为:
。所以第k步消元乘除法运算总次数为
。完成
步消元乘除法运算总次数为
,回代过程乘除法的运算总次数为
。所以高斯消元法乘除法运算总次数为
,当n趋于无穷大,算法复杂度为
。
2.4结果测试
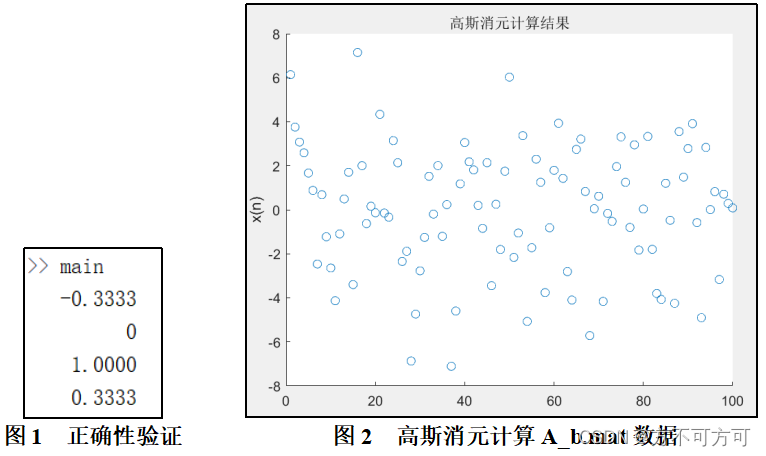
使用问题所给的矩阵A与向量b,求出的结果如图1所示,将结果代回线性方程组,可以验证得结果正确。导入附件A_b.mat数据,计算结果如图2所示。
3、用高斯消元法求矩阵A的逆
3.1高斯消元求A的逆思想
矩阵A、设的逆矩阵及单位矩阵I分别为:
设的每一列为
,
每一列为
,根据定理5:
,有:
。要求解逆矩阵
,则要求出每一个
,即求解线性方程组
。根据高斯消元法求解线性方程组的步骤,构造增广矩阵
并将
化成上三角矩阵,求出
后回代。
由于每求解一次都需要将矩阵A化成上三角矩阵,为了降低时间复杂度,构造一个矩阵
,将单位阵添加到A的右侧,这样以后,通过初等行变换直至将A化成上三角矩阵,就能得到每一个初等行变换后增广矩阵
,此时A矩阵只需经过一次化成上三角矩阵的过程。
3.2高斯消元求A的逆算法步骤
| 高斯消元法求A的逆
|
3.3算法复杂度分析
在完成步的消元过程中,使用高斯消元法求解线性方程组时,乘除法运算总次数为
,而在求解逆矩阵时,进行消元步骤矩阵的规模约为解线性方程组时的两倍,所以乘除法运算总次数约为
。
在回代过程中,求解线性方程组时乘除法的运算总次数为,而求解逆矩阵时要进行n次回代过程,所以乘除法运算总次数为
。
所以乘除法运算总次数约为。当n趋于无穷大,算法复杂度为
。
3.4结果测试
计算问题中给出A矩阵的逆,并计算
和
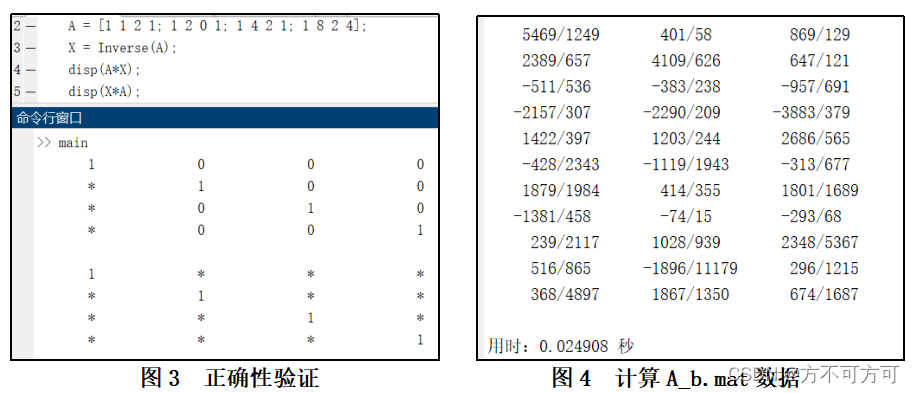
,所得结果都为单位矩阵,如图3所示,验证了算法正确性。导入A_b.mat数据,计算得部分结果如图4所示。
4、列主元消去法
4.1列主元消元法思想
列主元消元是基于高斯消元法的改进。在使用高斯消元法求解线性方程组时,在计算行乘数时若除数远远小于被除数,会造成较大误差。例如当A、b及的值为:
根据高斯消元法步骤,行乘数,增广矩阵变成:
得到,与实际值相比相差巨大。为了避免该情况,将第一行与第二行交换,得到
、行乘数
和
分别为:
回代得到,结果比高斯消元法精确。
4.2列主元消元法步骤
| 列主元消元法
|
4.3算法复杂度分析
列主元消元是在高斯消元的基础上增加了主元选取和交换两行的操作,而主元选取是在每一列对角线之下找到最大的元素,第k次选取时要比较次,一共需要比较
次。每次交换两行的时间复杂度为
,最坏情况为交换
次,时间复杂度为
。当n趋于无穷,高斯消元法求解线性方程组的时间复杂度为
,所以总的时间复杂度为
。
4.4结果测试
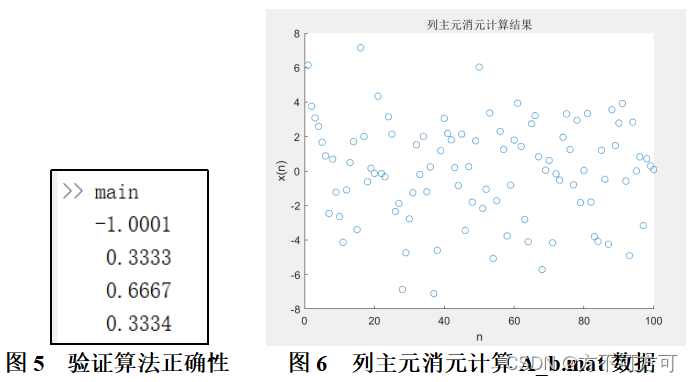
使用问题(3)中所给的B矩阵作为测试数据,运行代码得到结果如图5所示,将该结果代回线性方程组可验证得其正确性。导入A_b.mat数据之后,计算结果如图6所示。
5、高斯消元与列主元消元的差距
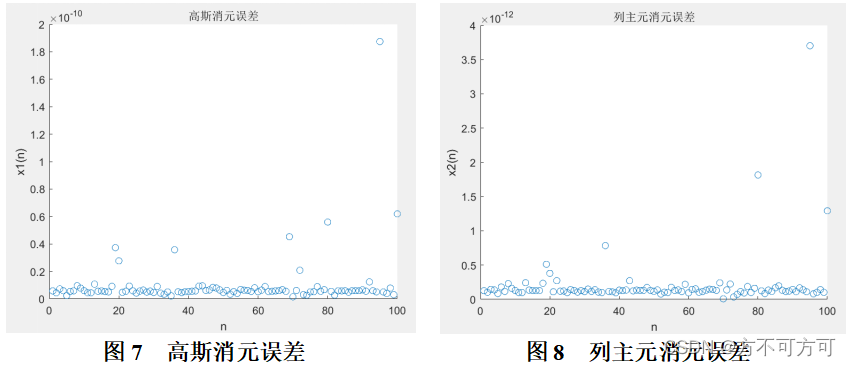
导入A_b.mat附件数据,分别计算高斯消元与列主元消元计算结果与准确值之间的差值的绝对值,除以准确值以计算误差,结果分别如图7、图8所示。可以看到列主元的误差比高斯消元的小两个数量级,列主元优化效果较明显。






















 482
482











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








