一、 实验目的与要求
1.掌握求解最小二乘法约束问题思路;
2.掌握建立数据拟合的优化模型;
3.掌握数学符号描述问题,设计算法求解模型。
二、 问题
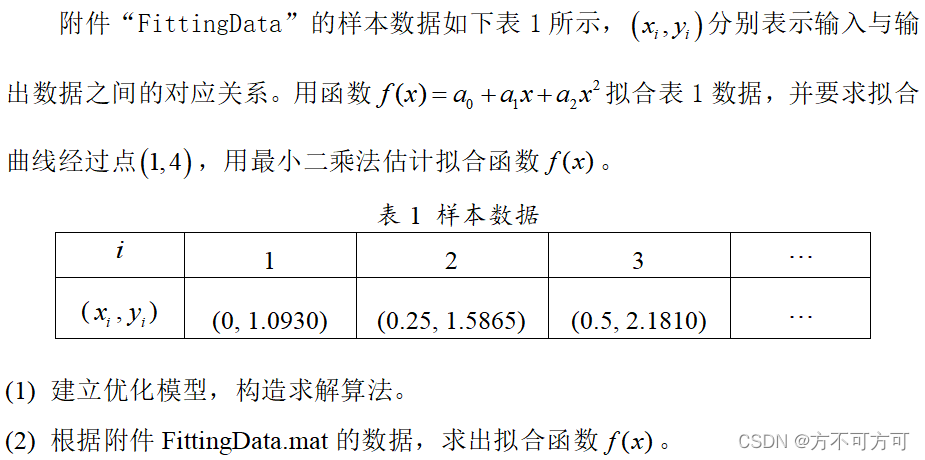
三、模型建立及求解
解决问题思路,算法实现描述,误差分析,存在问题等方面进行阐述。
1、定理、定义引入
Gram矩阵的定义:
若矩阵,则B为Gram矩阵。每个Gram矩阵都是半正定的,即
若要使Gram矩阵为正定的,则要满足:
即A是列向量无关的。正定矩阵都是非奇异的。
定理1:设函数f(x)在处可微,则
是
的必要条件
证明:将函数f(x)在处一阶泰勒展开,有:
令,
,可得:
当,则
,
,当t足够小,存在
,即:
若,则:
,与
矛盾,所以
得证。
是最优解问题
的必要条件但不是充分条件,因为
时,
有可能是最大值,故引入定理2:
定理2:若可微函数f(x)是凸函数,则是
的充要条件
定理1已证必要条件,现证充分条件,即:由于f(x)是可微且凸的,则
,有:
。
得证。
2、带约束条件的最小范数优化问题
对于有约束的优化问题,因为既有目标函数又要考虑约束条件,常常比较难以直接求解。如果能够将其转换为一个目标函数。而拉格朗日子乘法是一种常见的求解方法,可以将一般约束问题转化为等价的单个目标函数从而方便求解。

3、模型建立

4、模型求解

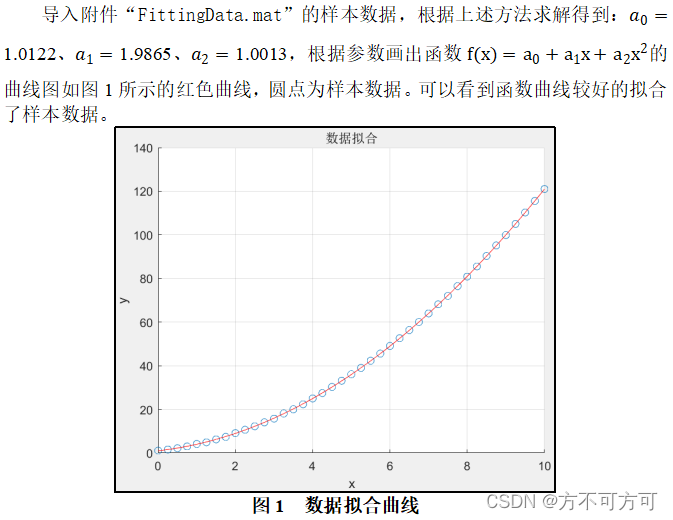
5、数据拟合






















 5254
5254











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








