目录
一、车辆纵向动力学模型

纵向受力分析:
:前轮的纵向轮胎力
:后轮的纵向轮胎力
:等效的纵向空气阻力
: 前轮胎的滚动阻力
:后轮的滚动阻力
:车辆质量
:重力加速度
:道路坡度角(上坡为正,下坡为负)
二、空气阻力
:空气的质量密度(与大气压力和空气温度有关系)
:空气阻力系数(通过风动测试获取,一般在0.22~0.32左右)
:车辆的正面投影面积(车辆在行驶方向上的投影面积,取宽*高的79%~84%)
:车辆的纵向速度
:风速(正值表示逆风,负值表示顺风)
不同速度下收到的阻力:
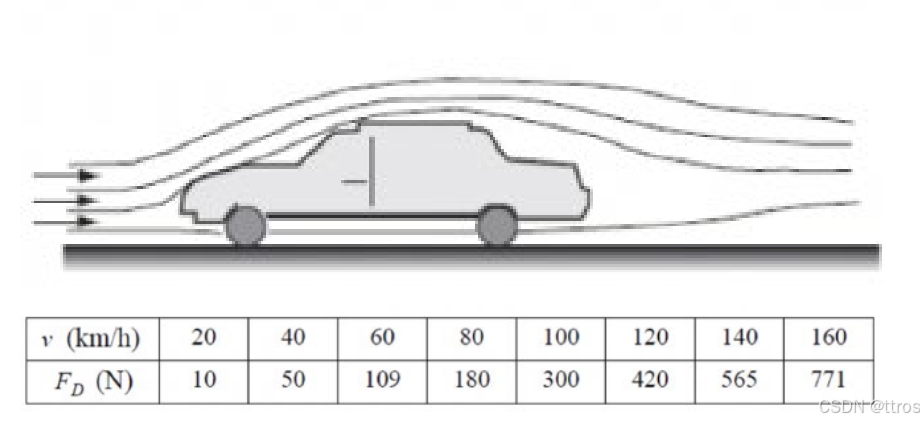
翼型车辆的气动阻力系数(左图),以及车辆车体随时间变化导致的阻力系数变化(右图):

三、纵向轮胎力
纵向轮胎力是地面作用于轮胎的摩擦力,每个轮胎产生的纵向力取决于以下因素:
1.滑动率
滑动率,即轮胎与地面相对运动的比例,其分为抱死时的滑移率和加速时的滑转率,两者共同描述轮胎的实际滑动情况。在轮胎正常滚动时为零,此时轮胎与地面间为静摩擦力。
滑动率定义为:
不同车轮状态下的滑动率分析
-
打滑:发生在车辆减速过程中(常规制动),此时
-
空转:发生在加速过程中(低摩擦路面,如结冰道路),此时
-
锁死:发生在紧急制动时(车辆失去期望的牵引力),此时
通过实验我们可以得到轮胎的纵向力与滑动率之间的关系,我们假设路面的这个摩擦系数为一个轮胎的法向载荷的常数,那轮胎纵向力就变成了滑动率的一个函数。如图在低滑动率的情况下,我们可以看到其实轮胎的纵向力和这个滑动率其实成正比的。而正比这部分的斜率,我们通常称为纵向刚度。前后轮的纵向刚度,我们就用和
来代表

高滑动率时需采用非线性轮胎模型,如魔术公式模型。感兴趣的可以看一下这篇博客,这里不详细讲
轮胎的魔术公式(Magic Fomula)模型 - 马语者 - 博客园
2.滚动阻力
车辆运行时,轮胎与地面接触会发生形变,导致滚动阻力。此阻力受车轮载荷、轮胎结构和材料、以及路面情况等因素影响。车重增加会增大轮胎变形,增加滚动阻力系数;轮胎轻薄且帘布层较少时,滚动阻力较小;路面越粗糙或积水越多,滚动阻力也越大。滚动阻力系数一般在0.01到0.04之间,子午线轮胎的系数约为0.015。
通常,滚动阻力被建模为与轮胎的法向力大致成正比,即:
其中 为滚动阻力系数。对于使用子午线轮胎的乘用车,典型值为 0.015。
和
分别为前轮和后轮的法向载荷(垂直力)。
左图为旋转静止中的轮胎,右图为旋转中的轮胎。

3.轮胎的法向载荷(垂直力 )
)
这里假设我们的这个车辆是以这个加速度在向前的加速,以后轮的接地中心为参考点,进行力矩平衡等式的建立。
前轮与后轮的法向力平衡方程如下:
法向力解析解:
其中为前轮到质心的距离
为后轮到质心的距离,
为质心高度,
为空气动力
的作用高度。
四、纵向控制器
-
定义:“纵向控制器”通常用于指代任何控制系统,该系统控制车辆的纵向运动。
-
控制状态:
-
纵向速度
-
加速度
-
纵向距离
-
-
控制输入:实施纵向控制的执行器:油门和刹车
-
实际应用:
-
自适应巡航控制
-
碰撞避免
-
自动化高速公路系统
-
五、PID控制器
非交互式(并行)的PID算法以传递函数形式表示为:
时域方程:
频域方程:
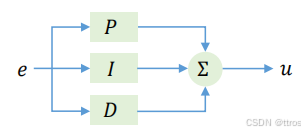
另一种常见于商用控制器的交互式(串联)形式为:

在实际应用中,我们需要根据测量量,噪音来设计不同形式的控制器
1.比例控制
对于纯比例控制,其控制律为:

比例控制器其实就是对这个误差进行了一个放大缩小,从而改变系统响应。比例控制中始终存在稳态误差。误差会随着增益增大而减小,但系统振荡倾向也会增强。为如下系统设计一个P控制器:
闭环传递函数为:
稳态分析:
越大,稳态误差越小,但相应的,初始状态的超调量就越大
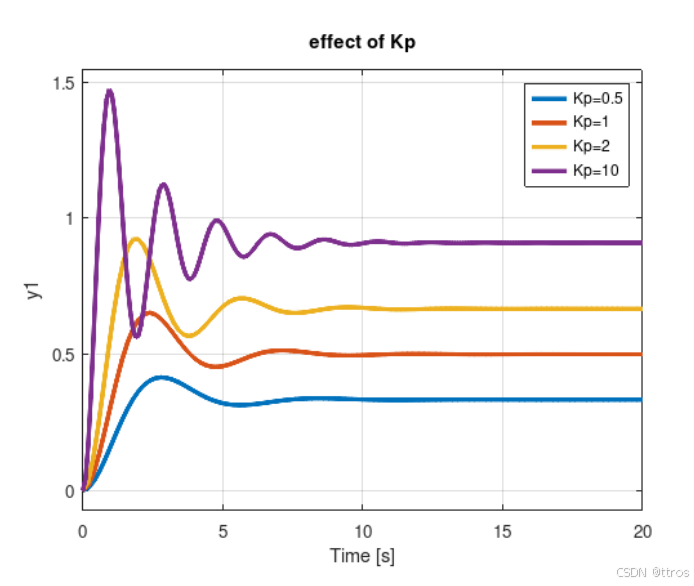
2.比例积分控制
比例部分能够立即改变输出,以在较短时间内响应误差并重新定位最终控制元件;而积分部分则会持续调整最终控制元件的位置,直至误差降至零。
积分模式的主要缺点是,控制器输出不会立即响应误差信号以重新定位最终控制元件。控制器输出的变化遵循预设的速率,因此需要一定时间才能完成最终控制元件的重新定位。
为如下系统设计一个PI控制器:
控制器形式为:
闭环传递函数为:
-
稳态分析:
-
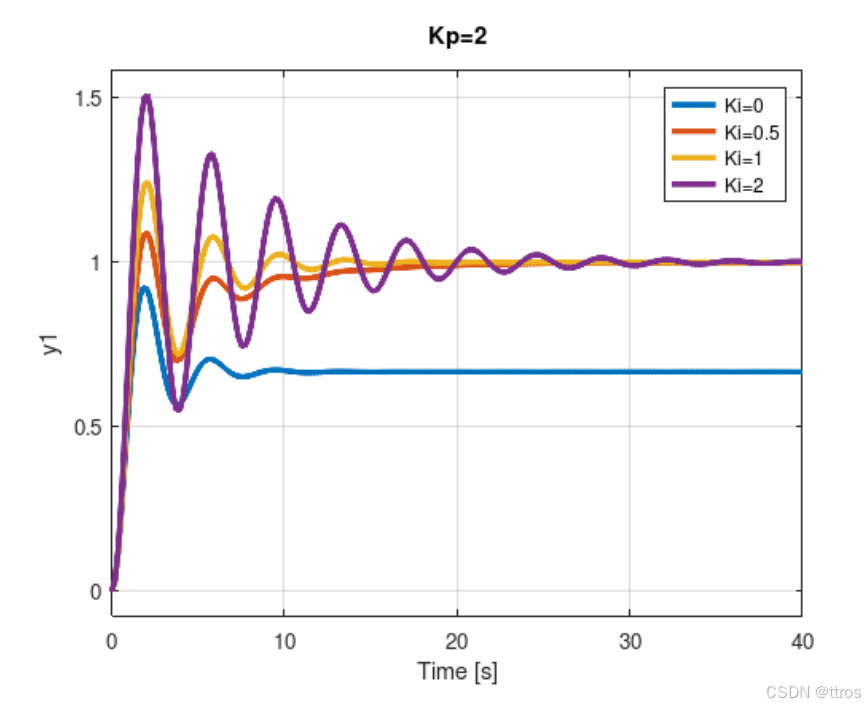
当
固定时,
越大,输出收敛到设定点的速度越快(如下图中红色与橙色曲线所示)。
-
但更高的
会导致系统产生更多振荡。
3.比例微分控制
-
误差信号的变化率越高,最终控制元件越能快速定位到期望值。
-
引入的微分作用可减少被测量变量的初始超调,从而帮助更快地稳定过程。
-
该控制模式称为比例加微分(PD)控制,因为微分部分响应误差信号的变化率
为如下系统设计一个PD控制器:
闭环传递函数为:
-
稳态分析:
-
当
固定时,
越大,系统的振荡越小。
-
但更高的
会导致收敛到设定点的速度变慢(如下图)。

4.PID算法的改进
(1) 微分项(D项)
考虑以下形式的PD控制器(其中 ):
时域方程为:
直接对误差信号 进行微分时,若误差信号存在高频噪声,直接对噪声信号进行微分会导致控制信号中出现剧烈的高频波动,可能引发系统不稳定。因此,需限制高频区域的增益。改进方法是将导数项实现为:
此式可视为理想导数项 通过一个时间常数为
的一阶系统滤波后的结果。
控制滤波器的截止频率(
),用于调节需要滤除的噪声频段。
越大,截止频率越高,保留的低频信号范围越宽。该近似方法仅在低频信号分量下保持导数作用,同时抑制高频噪声的影响。
(2) 积分项(I项)
积分饱和的定义:
积分饱和是指当控制器中的积分项因执行器(如电机、阀门)达到物理极限(如最大速度、全开/全闭状态)而无法继续调节时,积分项仍持续累积误差的现象。此时,控制信号超出执行器能力范围,导致系统反馈路径被破坏,积分项“卷绕”至极大值,引发超调或不稳定。
积分饱和的成因:
-
执行器饱和
执行器存在物理限制(如最大电压、转速、开度),当控制信号超过其极限时,输出被钳位(饱和),无法进一步响应误差变化。 -
积分项的持续累积
积分项在误差存在时不断累积,即使执行器已饱和,积分值仍持续增长。 -
反馈路径中断
执行器饱和后,其输出不再随误差变化,导致控制器与受控对象之间的闭环反馈失效,系统进入开环状态。
避免积分饱和的常用方法
1. 设定点限制
-
原理:通过斜坡设定点代替阶跃设定点,减少初始误差的急剧累积。
-
实现方式:

-
为斜坡斜率,需根据系统响应速度调整。
-
-
优点:简单易行,避免初始阶段的剧烈积分累积。
-
缺点:无法应对大干扰引起的饱和,且可能延长调节时间。
2. 积分钳位
-
原理:限制积分项的上下限,防止其无限增长。
-
实现方式:

-
和
根据执行器能力设定。
-
-
优点:直接限制积分项,防止极端值出现。
-
缺点:静态限幅可能降低控制精度,需动态调整限幅值。
3. 反计算法
-
原理:当执行器饱和时,将超出部分的控制量反馈到积分项中,动态修正积分累积。
-
实现步骤:
-
计算理论控制量:
-
实际输出:
-
计算饱和误差 :
-
修正积分项:
-
-
数学推导:
修正后积分项等效于反向抵消饱和误差的影响,使控制器更快退出饱和状态。 -
优点:动态调整积分项,兼顾响应速度与抗饱和能力。
-
关键参数:抗饱和系数
(即
),
越大,积分修正越强。
-
流程图:

六、PID 参数整定
1.Ziegler-Nichols (Z-N) 震荡法
1942 年由美国 Taylor 仪器公司的 Ziegler 和 Nichols 提出,是 PID 控制器最经典的工程整定方法之一。其通过实验方法(如临界增益法或震荡法)确定系统的临界增益 和震荡频率
,并基于经验公式计算 PID 参数。适用于低频稳定系统,通过调整增益使系统产生等幅震荡,进而整定参数。
Z-N 震荡法步骤:
-
初始化
-
将积分项
和微分项
设为 0。
-
将比例增益
设为较低值,确保系统稳定。
-
-
寻找临界增益
-
逐步增加
,直到系统出现等幅震荡(临界稳定状态)。
-
记录此时的临界增益
和震荡频率 f0f0。
-
-
计算 PID 参数
-
P 控制器:
-
PI 控制器:
-
PID 控制器:
-
参数修正与优化
-
四分之一衰减法
在 Z-N 方法基础上,通过调整使系统响应达到四分之一衰减(即每次震荡幅值减少 75%)。先调
使系统出现轻微震荡。记录震荡周期和幅值,逐步增加
和
优化响应。
-
超调量限制
对于不允许大超调的系统,可在 Z-N 方法基础上降低 或增加
,以减小超调。
2.其他方法
因篇幅有限,笔者在这里只介绍各自优缺点。
| 方法 | 优点 | 缺点 |
| 启发式调整 |
|
|
| Ziegler-Nichols调整方法 |
|
|
| Cohen-Coon调整方法 |
|
|
| Kappa-Tau调整方法 |
|
|
| Lambda调整方法 |
|
|
| 基于模型的调整 |
|
|
七、巡航控制
在标准巡航控制系统中,车辆的速度通过油门控制输入被调节至期望值。
-
系统目标:
保持车辆速度恒定,与驾驶员设定的目标速度一致。 -
输入输出关系:
-
输入:速度设定点(如驾驶员设定的 100 km/h)。
-
输出:系统通过调节油门开度或刹车力度生成期望加速度,使实际速度趋近目标值。
-
-
控制逻辑:
-
若实际速度 < 目标速度 → 增大油门(增加加速度)。
-
若实际速度 > 目标速度 → 减小油门或施加刹车(减小加速度)
-
一般来说我们把巡航控制分成两层来来对待。上层其实就是把目标速度的控制量转化成目标加速度。而下层就是如何得到追踪这个理想的目标加速度的油门和刹车的指令。
1.上层PI控制器
在设计上层PI控制器时,需要考虑由于底层控制器功率和带宽有限导致的动态响应不完美。为了更真实地模拟实际响应行为,假设使用一阶系统来描述底层控制器的动态行为。
一阶系统的加速度模型:
目标是从目标速度 控制目标加速度
的动态过程,并通过考虑物理限制,引入一阶系统来模拟目标加速度到实际加速度的转化。
一阶系统方程为:
速度与加速度之间的关系:
在频域中表示为:
结合一阶系统的传递函数:
目标速度与目标加速度之间的传递函数
将上述关系整理得到系统的传递函数:
控制器与系统模型
如图所示的控制框图:

控制器的数学表达式:
PI 控制器的传递函数为:
系统的受控对象描述了输入(控制信号)和输出(速度)之间的关系:
闭环系统的传递函数:
2.下层控制器
在下层控制器中,油门输入的计算旨在追踪上层控制器确定的目标加速度。其核心是建立加速度与油门/刹车操作之间的对应关系。
查表法:利用标定表直接映射速度、油门/刹车开度与加速度的关系。
查表法标定流程:
-
场景划分:
-
区分带拖挂、不带拖挂、拖挂负重等不同工况。
-
选择平坦长直道路,确保定位系统(如GPS)精度。
-
-
数据采集:
-
油门标定:
-
确定最小油门值(如12%对应2 m/s)和最大油门值(如30%对应20 km/h)。
-
按分档递增(如1%或2%)采集油门-速度-加速度数据。
-
-
刹车标定:
-
类似油门标定,分档测试刹车力度与减速度关系。
-
-
-
数据处理:
-
绘制油门-加速度曲线和刹车-减速度曲线,生成标定表(如图示)。
-
标定表精度与分档步长相关:步长越小,精度越高(但数据量增加)。
-
油门刹车标定表:

车辆模型法:
因为我们知道油门和刹车的开合度,其实直接是与引擎的扭矩相关的,其实是可以直接通过查表得到的。所以这里我们首先要建立起目标加速度与引擎扭矩之间的关系。
-
基本假设:
假设车辆速度直接与发动机转速相关:其中:
-
:轮胎有效半径
-
:车轮角速度
-
:传动比
-
:发动机输出轴角速度
-
-
纵向动力学模型:
其中:
-
:驱动力(由发动机输出扭矩转化而来)
-
:滚动阻力
-
:气动阻力
-
-
气动阻力建模:
气动阻力与车速的平方成正比,可表示为:其中
为气动阻力系数,与空气密度、车辆迎风面积和形状相关。
-
净扭矩:
目标加速度和我们的引擎扭矩之间的关系:
其中:
是反映到发动机侧的有效转动惯量。
其实可以看到,除了负载转变速比例、重力、重心位置,空气阻力,还有道路坡度等等这些原因,最重要的就是目标加速度,还有当前的速度。在这里可以看得出来,这个也符合油门标定中的方法的几个参数的选择。在实际应用中,除非是与这个汽车厂深度的合作,否则这些参数是其实比较难获得的,这里我们其实更希望的是通过对车辆模型的了解,知道为什么要做油门标定。
3.自适应巡航
我们知道定速巡航是根据驾驶员的要求的速度开关。开关开了之后,自动保持车速,而不用踩油门刹车。这样使得这个车辆以一个固定的速度行驶。我们都我们可以看得出来,就是定速巡航有一个很明显的缺点,也就是说它只能够提供一个相对固定的驾驶的速度的巡航。
输入:
- 驾驶员设定的速度
:类似于传统巡航控制的目标速度。
- 自车速度
:自车(ego car)的速度。
- 与前车的相对距离:即与前方车辆的距离(同车道)。
- 前车的相对速度:前车与自车的速度差。
- 时间间隙:车辆之间的时间间隔。
输出:
- 自车加速度:基于前述输入信息,ACC系统会输出自车的加速度,从而调整油门或刹车(与传统巡航控制类似)。
这套系统能够根据前车的速度、相对位置及驾驶员设定的目标速度,动态地调节车速,提升驾驶安全性与舒适性。
ACC系统有两种稳态操作模式:
-
速度控制模式(Speed control):
- 在此模式下,自车以驾驶员设定的速度行驶。
-
间距控制模式(Spacing control):
- 也称为车辆跟随模式(Vehicle following)。此模式下,自车会保持与前车的安全距离。
基本原理:
- 切换模式: 根据自车与前车的距离来选择控制模式。
- 过近(Too close): 如果自车离前车太近,则进入间距控制模式,目标是维持安全距离。
- 距离较远(Further away): 如果自车与前车的距离较远,则进入速度控制模式,目标是跟踪驾驶员设定的目标速度。
这些模式确保了ACC系统能够根据道路情况和前车行为灵活调整控制策略,提高安全性和舒适性。
安全距离:
自车与前车之间的安全距离是自车速度的函数,计算公式为:、
其中:
是安全距离。
是静止状态下的默认间距。
是车辆之间的时间间隔。
是自车的速度。
ACC 控制公式:
ACC系统的控制过程可以总结为两个不同的情况:
-
当相对距离小于安全距离时,使用间距控制:
-
当相对距离大于或等于安全距离时,使用速度控制:
其中:
是自车与前车的相对距离。
是设定的目标距离。
是驾驶员设定的目标速度。

八、代码实现
笔者使用的软件为LGSVL Simulator ,其是 LG 的硅谷实验室基于 Unity 引擎研发的一款开源自动驾驶模拟器。 可在ubuntu系统上与ROS进行联合仿真。
下面放一些纵向控制的核心代码:
vehicle_control.cpp
/*
* @Author: HaiChen
* @Date: 2025-02-03 15:25:10
* @LastEditors: Please set LastEditors
* @LastEditTime: 2025-02-03 18:05:39
* @Description: PID纵向控制
*/
#include "vehicle_control/common.h"
#include "vehicle_control/vehicle_control.h"
#include <fstream>
using namespace std;
static const rclcpp::Logger LOGGER = rclcpp::get_logger("vehicle_control_publisher");
// Controller
shenlan::control::PIDController yaw_pid_controller(0.5, 0.3, 0.1); // 转向角pid
shenlan::control::PIDController speed_pid_controller(1.0, 0.3, 0.0); // 速度pid
VehicleControlPublisher::VehicleControlPublisher() : Node("vehicle_control")
{
V_set_ = 10.0;//设置目标速度为10.0m/s
T_gap_ = 2.0;
first_record_ = true;
cout_distance_ = true;
cout_speed_ = true;
cnt = 0;
controller_frequency = 100;
qos = 10;// 设置服务质量等级,用于ROS 2的消息传递保证
vehicle_control_iteration_timer_ = this->create_wall_timer(10ms, std::bind(&VehicleControlPublisher::VehicleControlIterationCallback, this)); // 10ms根据 100Hz换算得到
localization_data_subscriber = this->create_subscription<nav_msgs::msg::Odometry>("/odom", qos, std::bind(&VehicleControlPublisher::odomCallback, this, _1));
vehicle_control_publisher = this->create_publisher<lgsvl_msgs::msg::VehicleControlData>("/vehicle_cmd", 1000);
// 初始化控制命令的时间戳为当前时间,设置目标档位为驱动档,目标车轮角度为0.0
control_cmd.header.stamp = this->now();
control_cmd.target_gear = lgsvl_msgs::msg::VehicleControlData::GEAR_DRIVE;
control_cmd.target_wheel_angle = 0.0;
// 读取参考线路径
std::ifstream infile;
infile.open("src/vehicle_control/data/SingleLaneRoad.txt"); //将文件流对象与文件连接起来
assert(infile.is_open()); //若失败,则输出错误消息,并终止程序运行
// 存储路径点的x和y坐标的向量
std::vector<std::pair<double, double>> xy_points;
std::string s;
std::string x;
std::string y;
while (getline(infile, s))
{
std::stringstream word(s);
word >> x;
word >> y;
double pt_x = std::atof(x.c_str());
double pt_y = std::atof(y.c_str());
xy_points.push_back(std::make_pair(pt_x, pt_y));
}
infile.close();
std::vector<double> headings; // 存储路径上每个点的方向角
std::vector<double> accumulated_s; // 存储路径上每个点的累积弧长
std::vector<double> kappas; // 存储路径上每个点的曲率
std::vector<double> dkappas; // 存储路径上每个点的曲率变化率
// 创建一个参考线对象,使用xy_points初始化,并计算路径特征
std::unique_ptr<shenlan::control::ReferenceLine> reference_line = std::make_unique<shenlan::control::ReferenceLine>(xy_points);
reference_line->ComputePathProfile(&headings, &accumulated_s, &kappas, &dkappas);
for (size_t i = 0; i < headings.size(); i++)
{
std::cout << "pt " << i << " heading: " << headings[i] << " acc_s: " << accumulated_s[i] << " kappa: " << kappas[i] << " dkappas: " << dkappas[i] << std::endl;
}
// 根据路径特征创建轨迹点,并添加到规划发布的轨迹中
for (size_t i = 0; i < headings.size(); i++)
{
TrajectoryPoint trajectory_pt;
trajectory_pt.x = xy_points[i].first;
trajectory_pt.y = xy_points[i].second;
trajectory_pt.v = 10.0;
trajectory_pt.a = 0.0;
trajectory_pt.heading = headings[i];
trajectory_pt.kappa = kappas[i];
planning_published_trajectory.trajectory_points.push_back(trajectory_pt);
}
trajectory_points_ = planning_published_trajectory.trajectory_points;
acceleration_cmd = 0.0;
yaw_cmd = 0.0;
}
VehicleControlPublisher::~VehicleControlPublisher(){}
/**
* @description: 返回轨迹上点到(x, y)的距离
* @param {TrajectoryPoint} &point
* @param {double} x
* @param {double} y
* @return {*}
*/
double VehicleControlPublisher::PointDistanceSquare(const TrajectoryPoint &point, const double x, const double y)
{
double dx = point.x - x;
double dy = point.y - y;
return dx * dx + dy * dy;
}
/**
* @description: 查询轨迹上距离(x, y)最近的点
* @param {double} x
* @param {double} y
* @return {*} trajectory_points_[index_min]
*/
TrajectoryPoint VehicleControlPublisher::QueryNearestPointByPosition(const double x, const double y)
{
double d_min = PointDistanceSquare(trajectory_points_.front(), x, y);
size_t index_min = 0;
for (size_t i = 1; i < trajectory_points_.size(); ++i)
{
double d_temp = PointDistanceSquare(trajectory_points_[i], x, y);
if (d_temp < d_min)
{
d_min = d_temp;
index_min = i;
}
}
cout << "vehicle.x: " << x << " " << "vehicle.y: " << y << endl;
cout << "trajectory_points.x: " << trajectory_points_[index_min].x << " " << "trajectory_points.y: " << trajectory_points_[index_min].y;
return trajectory_points_[index_min];
}
/**
* @description: 处理来自nav_msgs::msg::Odometry消息的数据
* @param {SharedPtr} msg
* @return {*}
*/
void VehicleControlPublisher::odomCallback(nav_msgs::msg::Odometry::SharedPtr msg)
{
// ROS_INFO("I heard: [%f]", msg->pose.pose.position.x);
// tf2::Quaternion q;
// tf2::quaternionMsgToTF(msg->pose.pose.orientation, q);
// tf2::Matrix3x3(q).getRPY(vehicle_state_.roll, vehicle_state_.pitch, vehicle_state_.yaw);
//使用tf2库将四元数转换为欧拉角,存储在vehicle_state_结构体中
tf2::Quaternion quat_tf;
tf2::convert(msg->pose.pose.orientation, quat_tf);
tf2::Matrix3x3(quat_tf).getRPY(vehicle_state_.roll, vehicle_state_.pitch, vehicle_state_.yaw);
if (first_record_)
{
vehicle_state_.start_point_x = msg->pose.pose.position.x;
vehicle_state_.start_point_y = msg->pose.pose.position.y;
//vehicle_state_.start_heading = vehicle_state_.yaw;
vehicle_state_.start_heading = -M_PI / 2;
first_record_ = false;
}
vehicle_state_.x = msg->pose.pose.position.x;
vehicle_state_.y = msg->pose.pose.position.y;
vehicle_state_.vx = msg->twist.twist.linear.x;
vehicle_state_.vy = msg->twist.twist.linear.y;
vehicle_state_.v = std::sqrt(vehicle_state_.vx * vehicle_state_.vx + vehicle_state_.vy * vehicle_state_.vy); // 本车速度
vehicle_state_.heading = vehicle_state_.yaw; // pose.orientation是四元数
}
/**
* @description: 执行车辆控制的迭代计算
* @return {*}
*/
void VehicleControlPublisher::VehicleControlIterationCallback()
{
TrajectoryPoint target_point_;
// 查询当前车辆位置最近的轨迹点
target_point_ = this->QueryNearestPointByPosition(vehicle_state_.x, vehicle_state_.y);
double v_err = target_point_.v - vehicle_state_.v; // 速度误差
double yaw_err = vehicle_state_.heading - target_point_.heading; // 横摆角误差
// 对横摆角误差进行限幅,防止过大的转向指令
if(yaw_err > M_PI / 6)
{
yaw_err = M_PI / 6;
}
else if(yaw_err < -M_PI / 6)
{
yaw_err = -M_PI / 6;
}
if (cnt % 20 == 0)
{
cout << "start_heading: " << vehicle_state_.start_heading << endl;
cout << "heading: " << vehicle_state_.heading << endl;
cout << "v_err: " << v_err << endl;
cout << "yaw_err: " << yaw_err << endl;
cout << "control_cmd.target_wheel_angle: " << control_cmd.target_wheel_angle << endl;
}
// 使用PID控制器计算加速度和横摆角
acceleration_cmd = speed_pid_controller.Control(v_err, 0.01);
yaw_cmd = yaw_pid_controller.Control(yaw_err, 0.01);
control_cmd.acceleration_pct = acceleration_cmd;
control_cmd.target_wheel_angle = yaw_cmd;
vehicle_control_publisher->publish(control_cmd);
cnt++;
}
int main(int argc, char** argv)
{
RCLCPP_INFO(LOGGER, "Initialize node");
rclcpp::init(argc, argv);
auto n = std::make_shared<VehicleControlPublisher>();
rclcpp::spin(n);
rclcpp::shutdown();
return 0;
}
pid_controller.cpp
#include "vehicle_control/pid_controller.h"
#include <assert.h>
namespace shenlan
{
namespace control
{
PIDController::PIDController(const double kp, const double ki, const double kd)
{
kp_ = kp;
ki_ = ki;
kd_ = kd;
previous_error_ = 0.0;
previous_output_ = 0.0;
integral_ = 0.0;
first_hit_ = true;
}
/**
* @brief 计算基于误差的控制值
* @param error 误差值,即期望值和测量值之间的差异
* @param dt 采样时间间隔
* @return 基于PID项的控制值
*/
double PIDController::Control(const double error, const double dt)
{
//这里的first_hit_决定是否有微分环节
if (first_hit_)
{
first_hit_ = false;
proportion_ = error;
integral_ += error * dt;
differential_ = 0.0;
}
else
{
proportion_ = error;
integral_ += error * dt;
differential_ = (error - previous_error_) / dt;
}
double output = kp_ * proportion_ + ki_ * integral_ + kd_ * differential_;
previous_output_ = output;
previous_error_ = error;
return output;
}
// 重置PID参数
void PIDController::Reset()
{
kp_ = 0.0;
ki_ = 0.0;
kd_ = 0.0;
previous_error_ = 0.0;
previous_output_ = 0.0;
proportion_ = 0.0;
integral_ = 0.0;
differential_ = 0.0;
}
} // namespace control
} // namespace shenlanpid_controller.h
/*
* @Author: HaiChen
* @Date: 2025-02-03 15:25:10
* @LastEditors: Please set LastEditors
* @LastEditTime: 2025-02-03 18:29:15
* @Description: 请填写简介
*/
#ifndef PID_CONROLLER_H
#define PID_CONTRLLER_H
namespace shenlan
{
namespace control
{
class PIDController
{
public:
PIDController(const double kp, const double ki, const double kd);
~PIDController() = default;
double Control(const double error, const double dt);
void Reset();
protected:
double kp_ = 0.0;
double ki_ = 0.0;
double kd_ = 0.0;
double previous_error_ = 0.0;
double previous_output_ = 0.0;
double proportion_ = 0.0;
double integral_ = 0.0;
double differential_ = 0.0;
bool first_hit_ = false;
};
} // namespace control
} // namespace shenlan
#endif























 6404
6404

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








