机器学习之支持向量机（SVM)

饺子馅儿～

已于 2024-06-11 20:25:58 修改

阅读量818

点赞数 30

文章标签：机器学习支持向量机算法

于 2024-06-11 14:56:47 首次发布

本文链接：https://blog.csdn.net/m0_73231314/article/details/139596525

版权

一、支持向量机

1.1定义

支持向量机是一种监督式学习的方法，按照监督学习（supervised learning）的方式对数据进行分类或回归。
它是一类广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplane）。
SVM通过寻找支持向量（即距离超平面最近的数据点）来确定最优的超平面，这些支持向量对于分类决策起着关键作用。

1.2分类

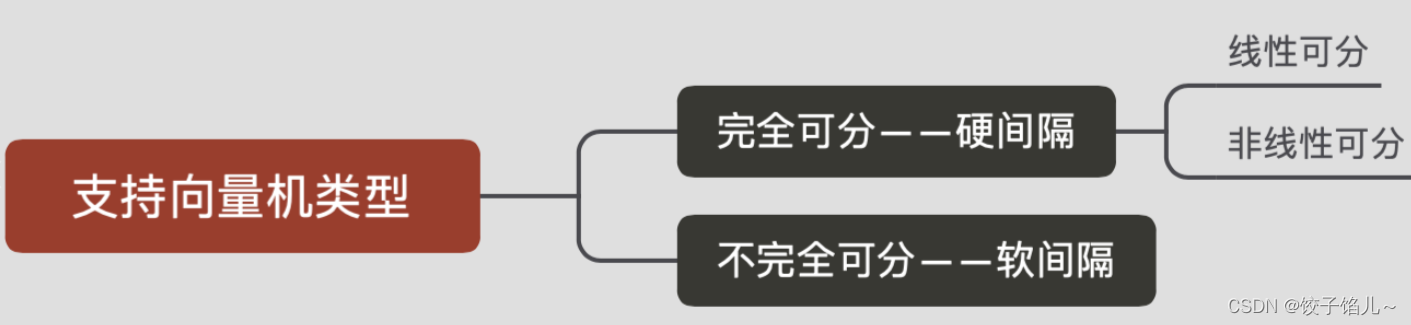
1.3优缺点

优点：

泛化能力强：SVM以统计学习理论为基础，采用结构风险最小化原则，因此具有良好的泛化能力和推广性能。这意味着SVM能够在处理未知数据时保持较高的准确性。
全局最优解：SVM的求解过程是一个凸二次规划问题，这保证了可以得到全局最优解，从而确保了解的有效性。
处理高维数据：SVM通过巧妙地构造核函数，能够克服特征空间中的维数灾难问题。它只需要在原空间中计算样本数据与支持向量的内积，而不需要知道非线性映射的显性表达形式，从而有效地处理高维数据。
适用于小样本数据：SVM的分类效果不仅与训练样本的数量有关，还与样本的分布情况有关。在样本量不是海量数据的情况下，SVM的分类准确率高。
可以处理非线性问题：通过选择合适的核函数，SVM可以将非线性问题转化为线性问题进行处理，从而扩大了其应用范围。

缺点：

对参数敏感：SVM的性能受到多个参数（如核函数的选择、正则化参数等）的影响。这些参数的选择对分类结果有较大的影响，需要进行反复试验和调整。如果参数选择不当，可能会导致分类效果较差。
计算复杂度高：尤其是对于大规模数据集和高维数据集，SVM的计算时间和计算空间需求都会很大。此外，训练过程需要多次迭代，也会增加计算的复杂度。
对噪声数据敏感：如果数据中存在噪声或孤立点，可能会对SVM的分类结果造成不良影响。因此，在使用SVM进行分类之前，通常需要对数据进行预处理以去除噪声。
仅适用于二分类问题：原始的SVM是设计用来解决二分类问题的。虽然可以通过构造多个二分类器来解决多分类问题，但效果可能并不理想。

二、基本概念

2.1线性可分

对于一个数据集合可以画一条直线将两组数据点分开，这样的数据称为线性可分，如下图：

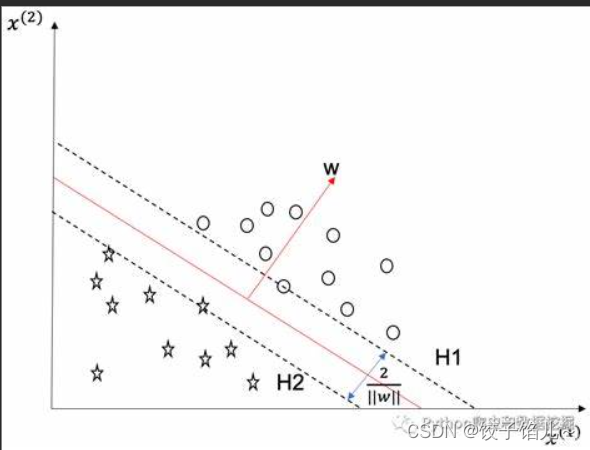
2.2平面与间隔

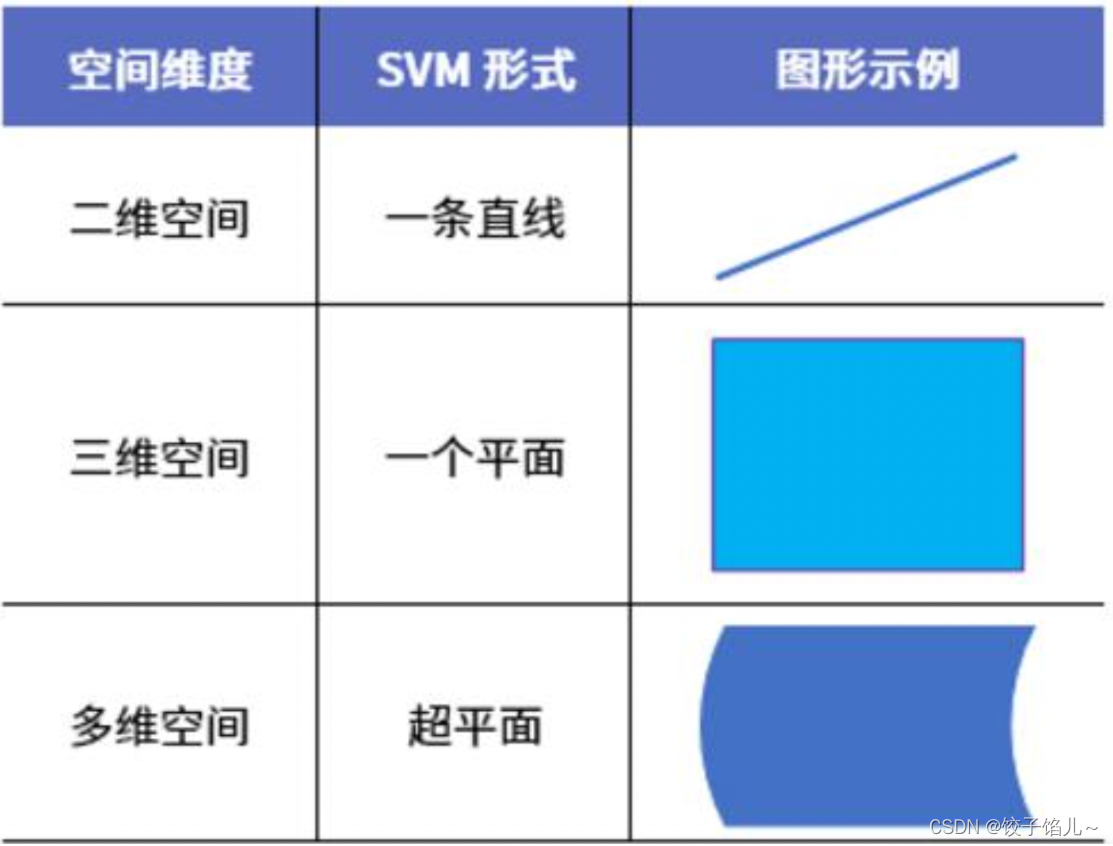
1.超平面：对于三维及三维以上的数据来说，分隔数据的是个平面，称为超平面，也就是分类的决策边界。

2.分割超平面：将上述数据集分隔开来的直线成为分隔超平面。对于二维平面来说，分隔超平面就是一条直线。

3.间隔：数据集所有点到分隔面的最小间隔的2倍，称为分类器或数据集的间隔。论文中提到的间隔多指这个间隔。SVM分类器就是要找最大的数据集间隔。

4.点相对于分割面的间隔：点到分割面的距离，称为点相对于分割面的间隔。

5.支持向量：离分隔超平面最近的那些点。

三、寻找最大间隔

3.1分割超平面

二维空间一条直线的方程为，y=ax+b，推广到n维空间，就变成了超平面方程，即 $f(x)=w^{T}x+b$ ，其中w是权重，b是截距，训练数据就是训练得到权重和截距。

3.2决定最好参数

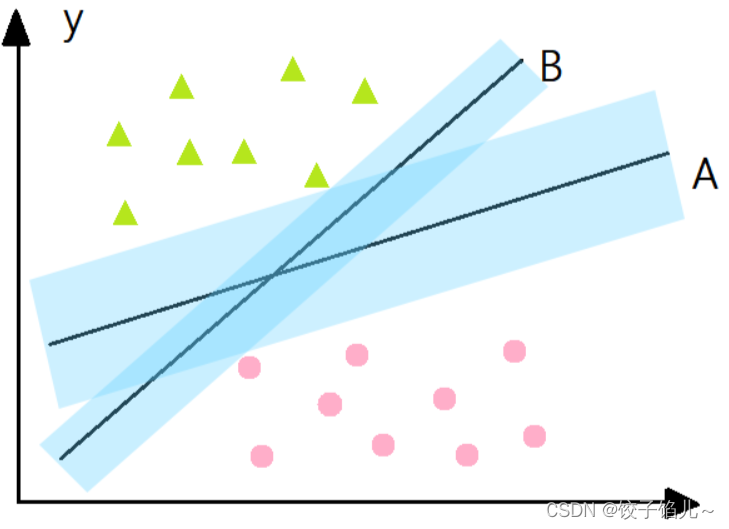
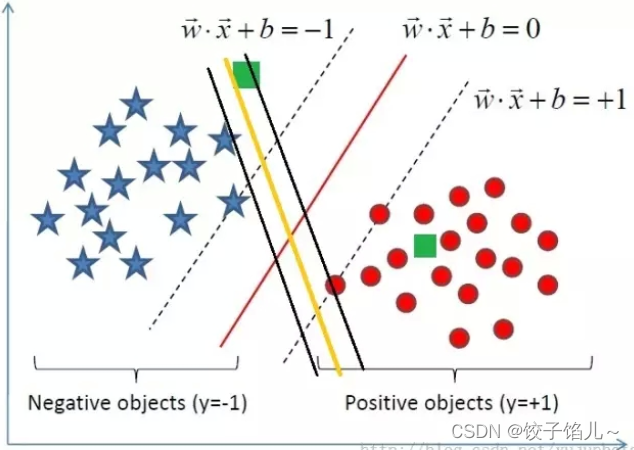
SVM划分的超平面：f(x) = 0，w为法向量，决定超平面方向，
假设超平面将样本正确划分
　　f(x) ≥ 1，y = +1
　　f(x) ≤ −1，y = −1
间隔：d=2/|w|

最大化间隔也就是寻找参数w和b , 使得下述公式最大：

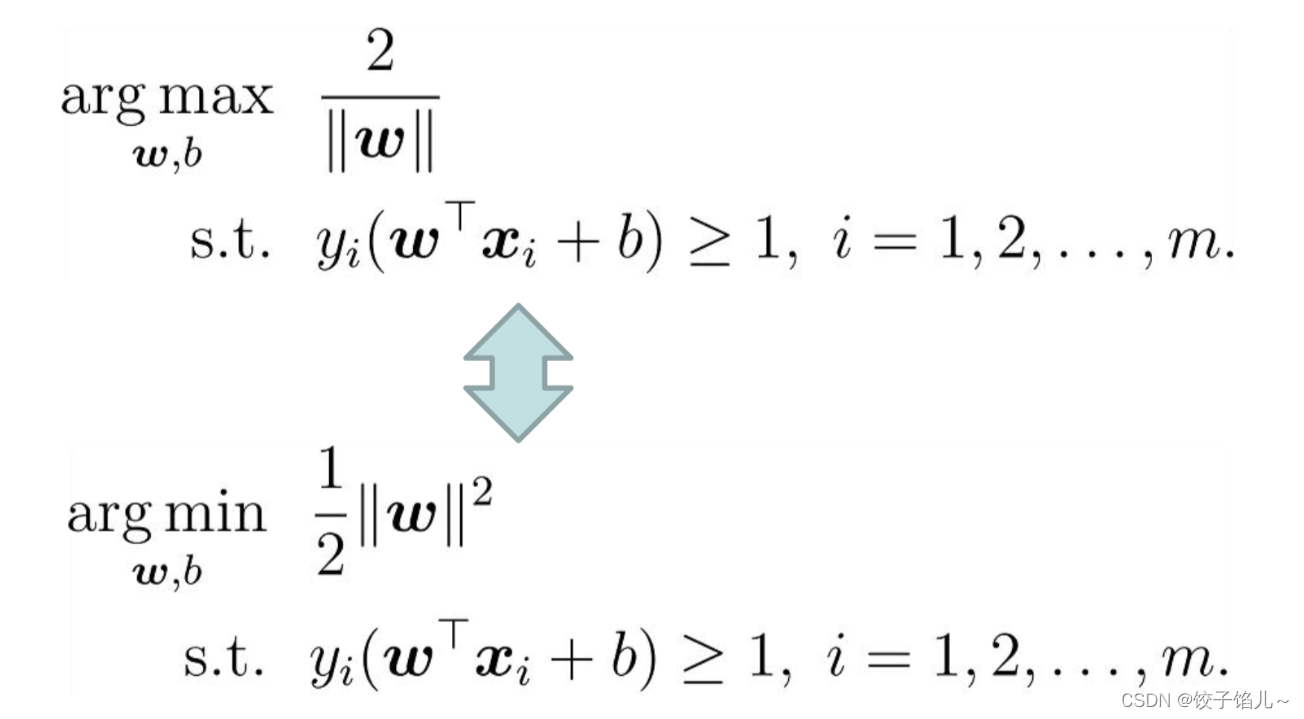
四、对偶问题

4.1KKT条件

KKT条件（Karush-Kuhn-Tucker Conditions）是在优化问题中，特别是在具有约束条件的优化问题中，一个非常重要的概念。

KKT条件主要包括三个部分：
1. 原问题的约束条件：包括等式约束和不等式约束。
2. 拉格朗日函数的梯度为零：即∇_xL(x, λ, ν) = 0，其中L(x, λ, ν)是拉格朗日函数，λ和ν是拉格朗日乘子。
3. 拉格朗日乘子的非负性：对于不等式约束，对应的拉格朗日乘子λ_i必须非负，即λ_i ≥ 0。
公式表示（示例）：
- 对于一个标准优化问题（原问题）：
  - min f_0(x)
  - s.t. f_i(x) ≤ 0, i = 1, ..., m
  - h_i(x) = 0, i = 1, ..., p
- 对应的拉格朗日函数为：
  - L(x, λ, ν) = f_0(x) + ∑_{i=1}m λ_i f_i(x) + ∑_{i=1}p ν_i h_i(x)
  - 其中，λ_i ≥ 0 是对应不等式约束的拉格朗日乘子，ν_i 是对应等式约束的拉格朗日乘子。

4.2拉格朗日乘法

支持向量机的目标函数与约束函数：

$\underset{w,b}{argmin}\frac{1}{2}\left \| w \right \|^{2}$

$s.t.$ $y_{i}(w^{T}x_{i}+b)\geq 1,i=1,2,...m$

第一步：引入拉格朗日乘子 $a_{i}$ ≥0得到拉格朗日函数
$L(w,b,\alpha )=\frac{1}{2}\left \| w \right \|^{2}-\sum_{i=1}^{m}\alpha _{i}(y_{i}(w^Tx_{i}+b)-1)$
第二步：令L(w,b,α)

$w=\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}$ ， $\sum_{i=1}^{m}\alpha _{i}y_{i}=0$

第三步：w,b回代到第一步

$\underset{\alpha }{min}\frac{1}{2}\sum_{i=1}^{j=1}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}^Tx_{j}-\sum_{i=1}^{m}\alpha _{i}$

$\sum_{i=1}^{m}\alpha _{i}y_{i}=0,\alpha _{i}\geq 0,i=1,2,...,m$

第四步：转换为对偶形式

$\underset{\alpha }{max}\frac{1}{2}\sum_{i=1}^{m}\alpha _{i}-\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}^Tx_{j}$

$\sum_{i=1}^{m}\alpha _{i}y_{i}=0$

第五步：最终模型

$f(x)=w^Tx+b=\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}^Tx+b$ ，其中未知数为 $a_{i}$

五、核函数

核函数（Kernel Function）是用于将输入空间中的数据点映射到特征空间中的函数。它通过某种非线性变换φ(x)，将原始数据映射到高维空间，使得在这个高维空间中数据点之间的关系可能更加明显，从而更容易被线性算法处理。

5.1常用核函数

1、线性核。就表示原空间内积，适用于线性可分问题。
$\kappa (x_{i},x_{j})=x_{i}^Tx_{j}$
2、高斯核。适用于没有先验经验的非线性分类。其中σ越小，使得映射的维度越高。
$\kappa (x_{i},x_{j})=exp(-\frac{\left \| x_{i}-x_{j} \right \|^2}{2\sigma ^2})$
3、多项式核。适用于没有先验经验的分类。其中d越越小，使得映射的维度越高。
$\kappa (x_{i},x_{j})=(\alpha x_{i}^Tx_{j}+c)^d$
4、Sigmoid核。此时SVM实现的就是一种多层感知器神经网络。
$\kappa (x_{i},x_{j})=tanh(\alpha x_{i}^Tx_{j}+c)$

5.2特点

线性核函数：简单，求解快，奥卡姆剃刀，可解释性强。

高斯核函数：可以映射到无限维，决策边界更多样，只有一个参数，更容易选择，特征多时会选用。但可解释性差，容易过拟合，计算速度较慢。

多项式核函数：可解决非线性问题，参数较多，对大数量级特征不适用。

Sigmoid核函数：主要用于神经网络。

六、SMO算法

主要用于解决SVM目标函数的最优化问题，特别是当数据集规模较大时，SMO算法能够高效地找到最优解。

6.1基本思路

选择两个变量：
- 根据某种启发式方法（如序列最小化原则）选择两个变量进行优化。
求解子问题：
- 在固定其他变量的前提下，对选定的两个变量进行求解，得到新的值。
迭代优化：
- 不断重复步骤1和步骤2，直到满足终止条件（如达到最大迭代次数或函数值收敛）。

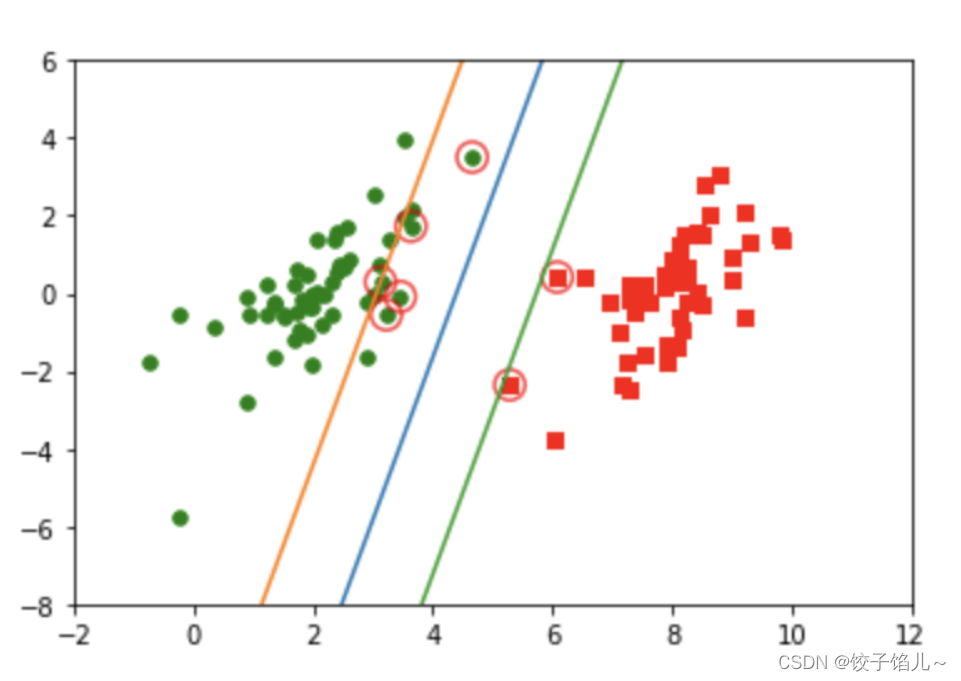
6.2应用简化版SMO算法结果图示

数据集：

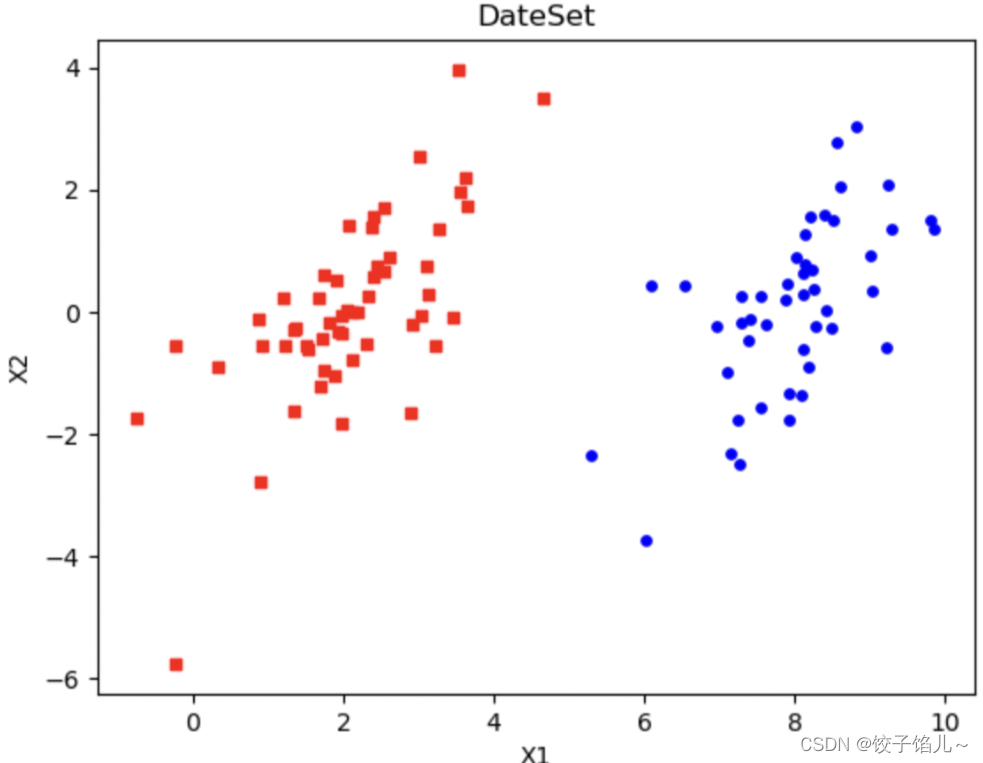
SMO算法进行求解：

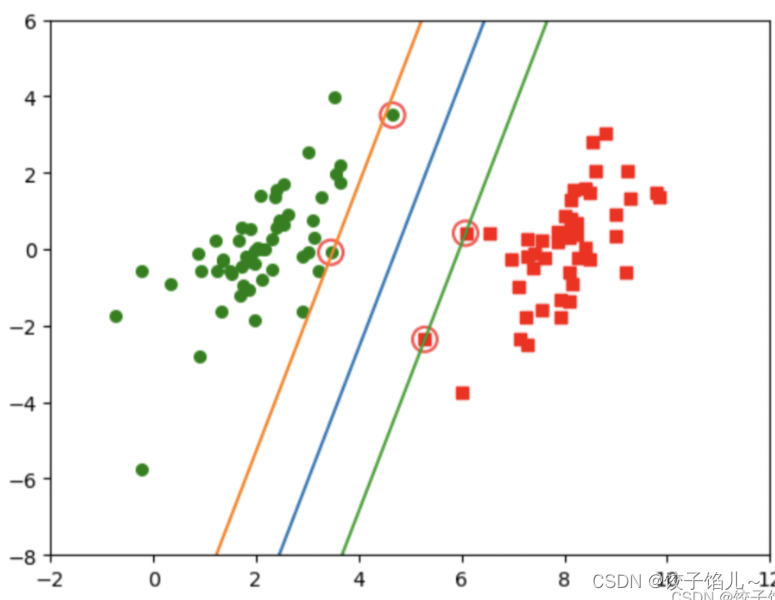
优化：

七、代码实例（鸢尾花分类测试）

7.1数据集介绍

鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例。数据集内包含 3 类共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）三种中的哪一品种。

#数据内容

     sepal_len  sepal_wid  petal_len  petal_wid  label
0          5.1        3.5        1.4        0.2      0
1          4.9        3.0        1.4        0.2      0
2          4.7        3.2        1.3        0.2      0
3          4.6        3.1        1.5        0.2      0
4          5.0        3.6        1.4        0.2      0
..         ...        ...        ...        ...    ...
145        6.7        3.0        5.2        2.3      2
146        6.3        2.5        5.0        1.9      2
147        6.5        3.0        5.2        2.0      2
148        6.2        3.4        5.4        2.3      2
149        5.9        3.0        5.1        1.8      2

7.2代码实现

1.源代码：

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
 
 
 
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
 
    df.columns = ['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'label']
    print(df)
 
    data = np.array(df.iloc[:100, [0, 1, -1]])
 
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
 
    return data[:,:2], data[:,-1]
 
 
class SVM:
    def __init__(self, max_iter=100, kernel='poly'):
        self.max_iter = max_iter
        self._kernel = kernel
 
    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
 
        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 松弛变量
        self.C = 1.0
 
    def _KKT(self, i):
        y_g = self._g(i)*self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1
 
    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j]*self.Y[j]*self.kernel(self.X[i], self.X[j])
        return r
 
    # 核函数
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k]*x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k]*x2[k] for k in range(self.n)]) + 1)**2
 
        return 0
 
    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]
 
    def _init_alpha(self):
        # 外层循环首先遍历所有满足0<a<C的样本点，检验是否满足KKT
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)
 
        for i in index_list:
            if self._KKT(i):
                continue
 
            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j
 
    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha
 
    def fit(self, features, labels):
        self.init_args(features, labels)
 
        for t in range(self.max_iter):
            # train
            i1, i2 = self._init_alpha()
 
            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1]+self.alpha[i2]-self.C)
                H = min(self.C, self.alpha[i1]+self.alpha[i2])
            else:
                L = max(0, self.alpha[i2]-self.alpha[i1])
                H = min(self.C, self.C+self.alpha[i2]-self.alpha[i1])
 
            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2*self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                # print('eta <= 0')
                continue
 
            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E2 - E1) / eta
            alpha2_new = self._compare(alpha2_new_unc, L, H)
 
            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
 
            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new-self.alpha[i2])+ self.b
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new-self.alpha[i2])+ self.b
 
            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2
 
            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new
 
            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
        return 'train done!'
 
    def predict(self, data):
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
 
        return 1 if r > 0 else -1
 
    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)
 
    def _weight(self):
        # linear model
        yx = self.Y.reshape(-1, 1)*self.X
        self.w = np.dot(yx.T, self.alpha)
        return self.w
 
 
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
 
 
svm = SVM(max_iter=800)
print(svm.fit(X_train, y_train))
print(svm.score(X_train, y_train))
print(svm.score(X_test, y_test))

2.基于sklearn的代码实现

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
 
 
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    return data[:,:2], data[:,-1]
 
 
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
 
 
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.show()
 
 
model = SVC()
model.fit(X_train, y_train)
 
SVC(C=1.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='scale', kernel='rbf',
    max_iter=-1, probability=False, random_state=None, shrinking=True,
    tol=0.001, verbose=False)
 
 
print('train accuracy: ' + str(model.score(X_train, y_train)))
print('test accuracy: ' + str(model.score(X_test, y_test)))

7.3运行结果

1.数据分布

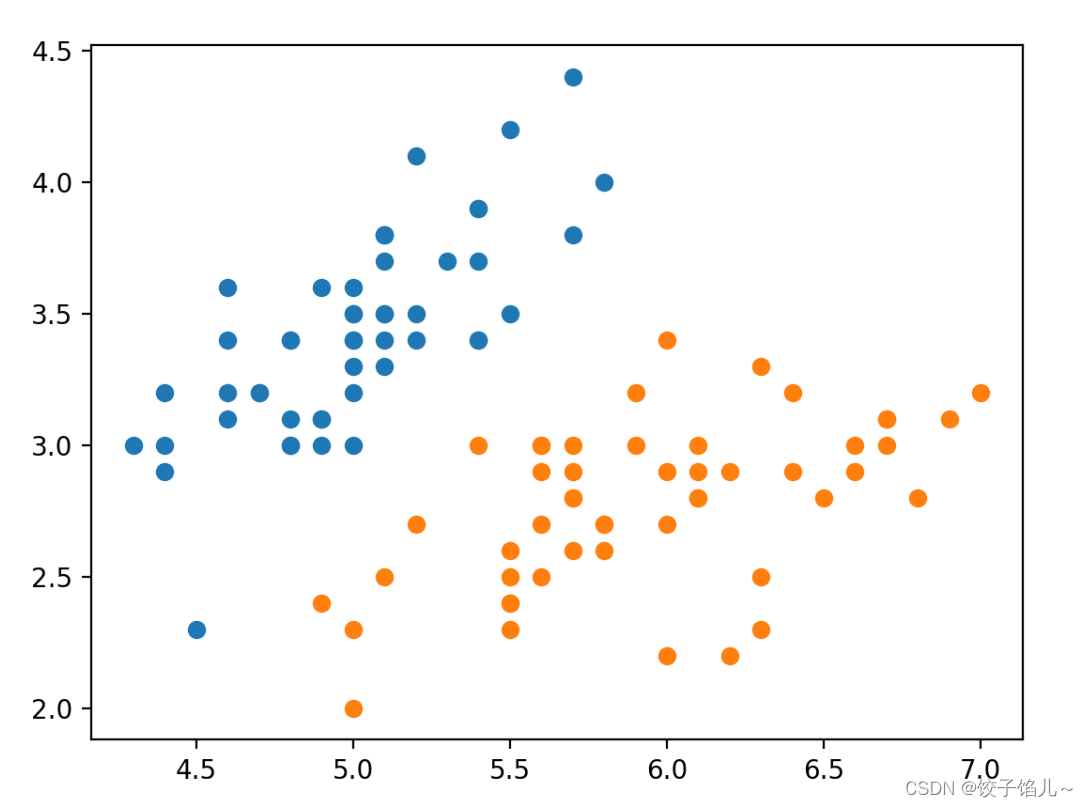
2.训练集和测试集上的准确性

train accuracy: 1.0
test accuracy: 0.96

八、问题及总结

8.1问题

运行时报错

ValueError：setting an array element with a sequence. The requested array has an inhomogeneous shape after 1 dimensions. The detected shape was (2,) + inhomogeneous part.

解决方法：降低numpy版本后成功运行。

8.2总结

支持向量机（SVM）是一种强大的监督学习算法，用于分类和回归分析。以下是关于SVM的总结：

目标：SVM的主要目标是找到一个最佳的超平面，能够将数据集中的不同类别分开，并且使得边界（或者称为间隔）尽可能地远离训练数据点，从而提高泛化能力。
核函数：SVM可以使用核函数来处理非线性可分的数据。常见的核函数包括线性核、多项式核和高斯径向基函数（RBF）核。
支持向量：在SVM中，支持向量是指离超平面最近的那些数据点，它们对于定义决策边界起着关键作用。由支持向量决定了最终的超平面位置。
软间隔与硬间隔：SVM可以通过软间隔来处理一些噪声数据或者存在一定程度重叠的情况，这时允许一些数据点落在间隔内部，但会引入惩罚项来控制错误分类的数量。
正则化参数：SVM中的正则化参数C用于平衡间隔的最大化和误分类的惩罚，较大的C会导致更严格地要求所有样本都正确分类，而较小的C会允许一些样本被错分。
多类别分类：SVM最初是为二元分类设计的，但可以通过一对一或一对其他的方法扩展到多类别分类问题。

总的来说，SVM是一种多功能的机器学习算法，它在处理小样本、非线性和高维数据上表现出色，并且具有很强的泛化能力。然而，SVM的计算复杂度随着训练集大小的增加而显著增加，因此在处理大规模数据时需要谨慎使用。

饺子馅儿～

关注

30
点赞
踩
24

收藏

觉得还不错? 一键收藏
1
评论
机器学习之支持向量机（SVM)

鸢尾花数据集是一个经典数据集，在统计学习和机器学习领域都经常被用作示例。数据集内包含 3 类共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica）三种中的哪一品种。#数据内容运行时报错解决方法：降低numpy版本后成功运行。支持向量机（SVM）是一种强大的监督学习算法，用于分类和回归分析。
复制链接

扫一扫