密度峰值聚类(DPC)算法的介绍

最新推荐文章于 2024-07-15 16:53:47 发布

木南木

最新推荐文章于 2024-07-15 16:53:47 发布

阅读量4.8k

点赞数 9

文章标签：算法聚类机器学习

本文链接：https://blog.csdn.net/m0_74086448/article/details/131635573

版权

DPC算法

密度峰值聚类算法（Density Peak Clustering Algorithm）是一种无监督的聚类算法，它能够自动发现数据中的密度峰值点，并根据这些峰值点将数据进行聚类。该算法由Alex Rodriguez和Alessandro Laio于2014年提出，其原理相对简单但非常有效。

密度峰值聚类算法基于两个重要的概念

局部密度（ $\rho$ ）：局部密度指的是一个数据点周围一定半径范围内的数据点数量，可以用来描述该点的密集程度。对于每个数据点，需要计算它的局部密度。
相对距离（ $\delta$ ）：相对距离指的是一个数据点与比它密度(ρ)更大的点之间的相对距离。一般采用欧式距离。

具体实现

有了这两个概念后，我们需要计算出所有数据点的局部密度 $\rho$ 与相对距离 $\delta$ ，当 $\rho$ 与 $\delta$ 都大时，我们即将该点定义为密度峰值(类簇中心)，然后将将剩余数据点分配给密度比它高的最近数据点所在类簇。

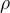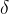$\rho$ 与 $\delta$ 的计算

局部密度（ $\rho$ ）表示一个数据点周围一定半径范围内的数据点数量，用来描述该点的密集程度。在密度峰值聚类算法中，局部密度的计算方法如下：

$\rho_{i}= \sum K(dist_{(i,j)})$

其中， $K(dist_{(i,j)})$ 是一个核函数，用来衡量数据点i和j之间的距离dist(i, j)的影响。常见的核函数有高斯核函数（Gaussian kernel）、截断核函数（Truncated kernel）、Epanechnikov核函数等。这里可以根据具体需求选择合适的核函数。

采用不同的核函数后局部密度( $\rho$ )可表示为：

高斯核函数（Gaussian kernel）

$\rho_{i}=\sum_{j}^{}e^{-(\frac{d_{ij}}{d_{c}})^{2}}$
截断核函数（Truncated kernel）

$\rho_{i}=\sum_{j} \chi (d_{ij}-d_{c}) \; \; \; \; \; \; \; \; \; \; \chi (x)=\begin{cases} 1 & \text{ if } x<0 \\ 0 & \text{ if } x\geq 0 \end{cases}$

一般来说对于较大规模的数据集，截断核函数的聚类效果较好

而对于小规模数据集，高斯核函数的聚类效果更好

相对距离（ $\delta$ ）：

$\delta _{i}=\underset{j:\rho_{j}>\rho_{i}}{min}(d_{ij})$

代码实现

import numpy as np
import matplotlib.pyplot as plt

def distance(x, y):
    return np.linalg.norm(x-y)

def getDistanceMatrix(data):
    # 计算距离矩阵
    N, D = data.shape
    dists = np.zeros([N, N])
    for i in range(N):
        for j in range(N):
            dists[i, j] = distance(data[i,:], data[j,:])
    return dists

def select_dc(dists):
    # 计算dc，也可以手动输入，此处没有实现手动输入
    # 不使用np.percentile()，是因为dists有部分重复值、0值
    N, D = dists.shape
    dists_flat = np.reshape(dists, N*N)
    dists_sort = np.sort(dists_flat)
    position = int(N*(N-1)*0.02)
    # 将距离矩阵排序后取第2%个，可以调整该百分比使聚类效果更加
    dc = dists_sort[position+N]
    return dc

def calculate_rho(dists, dc, method=None):
    """
    计算ρ
    :param method:
    选择方法，默认为截断核
    传入任意参数，即可选择高斯核
    建议小规模数据选择高斯核，因为该方法计算出来带小数，比较更准确
       大规模数据选择截断核，效率更高
    """
    N = dists.shape[0]
    rho = np.zeros(N)
    # 截断核:(适合大规模数据)在dc区域内有多少个点
    if method == None:
        for i in range(N):
            for j in range(N):
                if dists[i, j] < dc:
                    rho[i] += 1
            rho[i] -= 1
        rho = np.sum(dists < dc, axis=1) - 1
        # 以上可以用向量化代替，效率更高
        # rho[i] = np.where(dists[i,:]<dc)[0].shape[0]-1

    # 高斯核:(适合小规模数据)
    else:
        for i in range(N):
            rho[i] = np.sum(np.exp(-(dists[i, :] / dc) ** 2)) - 1
    return rho


def calculate_deltas(dists, rho):
    # 计算δ
    N = dists.shape[0]
    deltas = np.zeros(N)
    nerghbers = np.zeros(N)         # 密度更高，且距离最近的 点的 索引
    for i in range(N):
        deltas[i] = dists[i, 0]     # 相当于中间值(可用一个大值代替，但不严谨)
        for j in range(N):
            # 要求满足， ρ更大 且 距离最近
            if rho[j] > rho[i] and dists[i, j] < deltas[i]:
                deltas[i] = dists[i, j]
                nerghbers[i] = j
    return deltas, nerghbers

def clusters(dists, rho, deltas, nerghbers, k = 0):
    """
    找出中心点并进行聚类，可分步
    :param k: 默认为0，代表自动确定中心点
              若传入值则确定多少个k中心点
    """
    N, D = dists.shape
    labels = np.full(N, -1)
    cluster = 0

    if k==0:
        # 自动确定中心点，并对中心点进行聚类
        # 设置聚类参数,可以使用np.percentile()函数取中位数
        rho_threshold = (np.min(rho)+np.max(rho))/2
        deltas_threshold = (np.min(deltas)+np.max(deltas))/2
        # rho_threshold = np.percentile(rho, 50)
        # delta_threshold = np.percentile(deltas, 50)
        for i in range(N):
            if rho[i] > rho_threshold and deltas[i] > deltas_threshold:
                labels[i] = cluster
                cluster += 1
                # 画中心点
                # plt.scatter(data[i,0], data[i,1], color="k", marker="+", s = 200)

    else:
        # 手动输入聚类数k,选择ρ*δ最大的k个，作为中心点，并聚类
        rho_deltas = rho*deltas
        center = np.argsort(-rho_deltas)
        for i in range(k):
            labels[center[i]] = i
            # 画中心点
            # plt.scatter(data[center[i], 0], data[center[i], 1], color="k", marker="+", s=250)

    # 对非中心点进行聚类
    # 从密度最高开始，将他们分给比它们密度更高且距离最近的点的类
    rho_sort = np.argsort(-rho)
    for i in rho_sort:
        if labels[i] == -1:
            labels[i] = labels[int(nerghbers[i])]
    return labels

def DPC(data,k):
    dists = getDistanceMatrix(data)
    dc = select_dc(dists)
    rho = calculate_rho(dists, dc, "gasstion")
    deltas, nerghbers = calculate_deltas(dists, rho)
    labels = clusters(dists, rho, deltas, nerghbers, k)

    # 画出rho与deltas
    for i in range(np.shape(data)[0]):
        plt.scatter(rho[i], deltas[i], s=16., color=(0, 0, 0))
        plt.annotate(str(i), xy=(rho[i], deltas[i]), xytext=(rho[i], deltas[i]))
        plt.xlabel("rho")
        plt.ylabel("deltas")
    plt.show()
    return labels

导入数据

data = np.loadtxt(r"data\data.txt")
labels = DPC(data,7)

画出 $\rho$ 与 $\delta$ 图像：

我们取最大的k个点作为类簇中心，再将剩下的点进行分类

聚类结果

聚类结果十分完美

其它数据聚类结果展示：

算法改进

参数选择的自动化：密度峰值聚类算法中需要选择一些参数，例如半径参数ε和截断参数c。改进的方法可以通过自动化的方式来选择这些参数，例如使用基于数据特征的方法或通过优化算法来寻找最优参数。
聚类中心选择策略：原始的密度峰值聚类算法选择密度峰值点作为聚类中心，但在某些情况下可能存在一些峰值点不适合作为聚类中心的情况。改进的方法可以考虑引入其他策略来选择聚类中心，例如根据密度和距离的综合考虑来选择最具代表性的数据点作为聚类中心。
密度估计方法改进：原始的密度峰值聚类算法使用核函数方法来估计局部密度，但核函数的选择和参数设定可能对聚类结果产生影响。改进的方法可以尝试其他密度估计方法，例如基于距离的方法或基于概率模型的方法，以提高密度估计的准确性。
噪声处理策略：密度峰值聚类算法对于噪声点比较敏感，噪声点可能会干扰聚类结果。改进的方法可以引入噪声处理策略，例如通过设置密度阈值或使用噪声剔除算法来过滤掉噪声点，以提高聚类的准确性和鲁棒性。
并行化加速：密度峰值聚类算法的计算量较大，可以考虑使用并行计算来加速算法的执行，提高算法的效率和可扩展性。

这些是一些对密度峰值聚类算法进行改进的可能方向。具体的改进方法可以根据具体需求和数据特点来选择和调整。改进后的算法可以更好地适应不同类型的数据集，并提供更准确和稳定的聚类结果。