算法导论----最大子数组问题(分治算法)

     在分治策略中，我们要递归地求解一个问题，每层递归包含三个步骤:

1.分解(Divide)将问题划分为一些子问题，子问题的形式与原问题一样，只是规模更小

2.解决(Conquer)递归地求解出子问题。如果子问题的规模足够小，则停止递归，直接求解

3.合并(Combine)步骤将子问题的解组合成原问题的解

当子问题足够大，需要递归求解时，我们称之为递归情况（rescursive case）。当子问题变得足够小，不再需要递归时，我们说递归已经“触底”，进入了基本情况(base case)。有时，除了与原问题形式完全一样的规模更小的子问题外，还需要求解与原问题不完全一样的子问题。我们将这些子问题的求解看做合并步骤的一部分。

     递归式:递归式就是一个等式或者不等式，它通过更小的输入上的函数值来描述一个函数。

    递归算法可以将问题分为规模不等的子问题，如2/3对1/3的划分。如果分解和合并步骤都是线性时间的，这样算法会产生递归式而且。这里和分别表示把总问题分成2/3和1/3所需时间。表示分解和合并的总时间。总时间可解得为。一般地，子问题的规模不必是原问题规模的一个固定比例。

    主方法的通式:，其中a>=1,b>1,是一个给定的函数。这种形式的递归式很常见，它刻画了这样一个分治算法:生成a个子问题，每个子问题的规模是原问题规模的1/b,分解和合并步骤总共花费时间为。

   我们偶尔会遇到不是等式而是不等式的递归式，例如。因为这样一种递归式仅描述了的一个上界，因此可以用大符号而不是符号来描述其解。类似地，如果不等式为，则由于递归式只给出了的一个下界，我们应使用符号来描述。

   递归式技术细节

   在实际应用中，我们会忽略递归式声明和求解的一些技术细节。例如，如果对n个元素调用MERGE-SORT(归并排序)，当n为奇数时，两个子问题的规模分别为和，准确来说都不是n/2，因为当n为奇数时，n/2不是一个整数。技术上，描述MERGE-SORT最坏情况运行时间的准确的递归式为   边界条件是另一类我们通常忽略的细节。由于对于一个常量规模的输入，算法的运行时间为常量，因此对于足够小的n,表示算法运行时间的递归式一般为。因此，处于方便，我们一般忽略递归式的边界条件，假设对很小的n，为常量。例如，该递归式可表示为。去掉了n很小时函数值的显式描述。原因在于，虽然改变的值会改变递归式的精确解，但改变幅度不会超过一个常数因子，因而函数的增长阶不会变化。

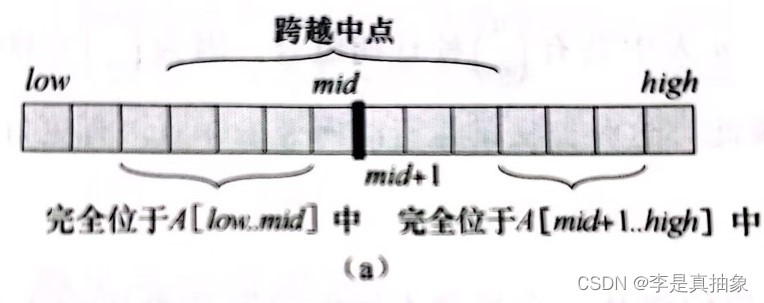
   我们来思考如何用分治技术来求解最大子数组问题。假定我们要寻找子数组A[low..high]的最大子数组。使用分治技术意味着我们要将子数组划分为两个规模尽量相等的子数组。也就是说，找到子数组的中央位置，比如mid，然后考虑求解两个子数组A[low..mid]和A[mid+1..high]。如图(a)所示，A[low..high]的任何连续子数组A[i..j]所处的位置必然是一下三种情况之一:

1.完全位于子数组A[low..mid]中，因此low<=i<=mid。

2.完全位于子数组A[mid+1..high]中，因此mid<i<=j<=high。

3.跨越了中点，因此low<=i<=mid<j<=high。

因此，A[low..high]的一个最大子数组所处的位置必然是这三种情况之一。实际上，A[low..high]的一个最大子数组必然是完全位于A[low..mid]中、完全位于A[mid+1..high]中或者跨越中点的所有子数组中和最大者。我们可以递归地求解A[low..mid]和A[mid+1..high]的最大子数组，因为这两个子问题仍是最大子数组问题，只是规模更小，因此，剩下的全部工作就是寻找跨越中点的最大子数组，然后在三种情况中选取和最大者。

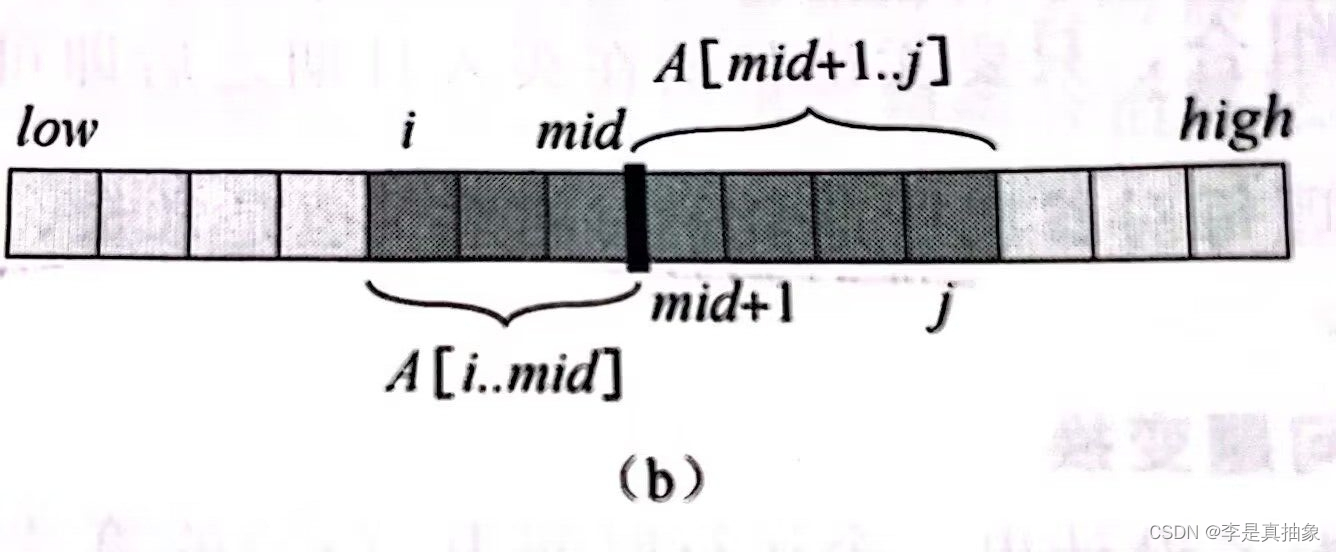
 如图(b)所示，任何跨越中点的子数组都有两个数组A[i..mid]和A[mid+1..j]组成。其中low<=i<=mid且mid<j<=high。因此，我们只需找出形如A[i..mid]和A[mid+1..j]的最大子数组，然后将其合并即可。过程FIND-MAX-CROSSING-SUVARRAY接收数组A和下表low、mid、和high为输入，返回一个下标元组划定跨越中点的最大数组的边界，并返回最大子数组中值的和。伪代码如下:

FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)

1 left_sum = 

2 sum=0

3 for i = mid downto low

4        sum = sum+A[i]

5         if sum>left_sum                           //这里是找到左半部分最大和，以及最大值所对应的数组                                                                      的最左边的数的索引，分别用left_sum和max_left记录

6                left_sum = sum

7                max_left = i

8 right_sum =

9 sum=0 

10 for j =mid +1 to high

11       sum = sum+A[j]

12       if sum>right_sum                         //这里是找到右半部分最大和，以及最大值所对应的数组                                                                      的最右边的数的索引，分别用right_sum和max_right记录

13              right_sum = sum

14              max_right = j

15 return (max_left,max_right,left_sum+right_sum)

      不难发现这里max_left和max_right没有初始化，其实它们在遍历过程中一定会被赋值。max_left最差与mid重合(mid值即为左子数组的最大子序列)，max_right最差与mid+1重合(mid+1值即为右子数组的最大子数组)。

      1-7行求出左半部分A[low..mid]的最大子数组。由于此子数组必须包含A[mid]，第3-7行的for循环的循环变量i是从mid开始，递减直至low，因此它所考察的每个子数组都具有A[i..mid]形式。10-14行同理。

     如果子数组A[low..high]包含n个元素(即n=high-low+1)，则调用FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)花费(n)时间。由于两个for循环的每次迭代花费(1)时间，我们只需统计一共执行了多少次迭代。第3-7行的for循环执行了mid-low+1次迭代，第10-14行的for循环执行了high-mid次迭代，因此总循环迭代次数为

             

分治算法伪代码如下:

FIND-MAXIMUM-SUBARRAY(A,low,high)

1 if high==low

2 return (low,high,A[low])

3 else mid=

4        (left_low, left_high,left_sum)=FIND-MAXIMUM-SUBARRAY(A,low,mid)

5        (right_low,right_high,right_sum)=FIND-MAXIMUM-SUBARRAY(A,mid+1,high)

6        (cross_low,cross_high,cross_sum)=FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)

7        if left_sum>=right_sum and left_sum>=cross_sum

8               return (left_low,left_high,left_sum)

9        elseif right_sum>=left_sum and right_sum>=cross_sum

10                return (right_low,right_high,right_sum)

11      else return (cross_low,cross_high,cross_sum)

具体C语言代码如下

#include<stdio.h>
#include<stdbool.h>
int Max(int a, int b, int c)
{
	if (a > b && a > c)return a;
	else if (b > a && b > c)return b; //求三个数的最大值
	else return c;
}
int FIND_MAX_CROSSING_SUBARRAY(int A[], int low, int high) //某个子问题的解决步骤
{
	int mid = (low + high) / 2;
	int sum = 0;
	int left_sum = -0x7fffffff;
	int right_sum = -0x7fffffff;
	int max_left;
	int max_right;
	for (int i = mid; i >= 0; i--)
	{
		sum += A[i];
		if (sum > left_sum)
		{
			left_sum = sum;
			max_left = i;
		}
	}
	sum = 0;
	for (int j = mid + 1; j <= high; j++)
	{
		sum += A[j];
		if (sum > right_sum)
		{
			right_sum = sum;
			max_right = j;
		}
	}
	return left_sum + right_sum;
}
int FIND_MAXIMUM_SUBARRAY(int A[],int low, int high)
{
	if (high == low)return A[low];
	int mid = (low + high) / 2;          //递归，将数组分成两半，求左半部分、右半部分最大值
	int max_left = FIND_MAXIMUM_SUBARRAY(A,low, mid);          //递归分治
	int max_right = FIND_MAXIMUM_SUBARRAY(A, mid + 1, high);   //递归分治
	int max_bordersum = FIND_MAX_CROSSING_SUBARRAY(A, low, high); //合并的步骤
	return Max(max_left, max_right, max_bordersum);//左边，右边，合并后，三者取最大值
}

该递归式为:其解为