【一】【动态规划NEW】1137. 第 N 个泰波那契数,面试题 08.01. 三步问题,使用最小花费爬楼梯

1137. 第 N 个泰波那契数

泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

示例 1：

输入：n = 4 输出：4 解释： T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4 示例 2：

输入：n = 25 输出：1389537

提示：

0 <= n <= 37 答案保证是一个 32 位整数，即 answer <= 2^31 - 1。

第$n$个泰波那契数等于第$n-1$个泰波那契数$+$第$n-2$个泰波那契数$+$第$n-3$个泰波那契数.
2.
用$dp[n]$表示第$n$个泰波那契数,$dp[i]$表示第 $i$ 个泰波那契数.
3.
当求解第$i$个泰波那契数即$dp[i]$的时候,很容易得到状态转移方程$dp[i]=dp[i-1]+dp[i-2]+dp[i-3]$.
4.
我们需要得到$dp[n]$的值.
5.
由状态转移方程,填写$i$位置状态,需要用到$i-1,i-2,i-3$位置状态,填表顺序应该是从小到大.
6.
特判,当$n==0$时,$dp[0]=0,n==1$时,$dp[1]=1,n==2$时,$dp[2]=1$.
也叫做初始化操作.

动态规划

class Solution {
public:
    int n; // 定义一个整数 n，用于存储目标的索引
    vector<int> dp; // 定义一个整型向量 dp，用于存储中间计算结果
    int ret; // 定义一个整数 ret，用于存储最终的结果
    void solve() { // 定义一个求解函数 solve
        dp.assign(n + 3, -1); // 初始化 dp 向量，大小为 n+3，初始值均为 -1
        ret = -1; // 初始化 ret 为 -1
        dp[0] = 0, dp[1] = 1, dp[2] = 1; // 初始化 dp 的前三个元素，分别为 0，1，1
        for (int i = 3; i <= n; i++) { // 从第 3 个元素开始，计算到第 n 个元素
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]; // 三数相加，得到当前元素的值
        }
        ret = dp[n]; // 最终结果赋值给 ret
    }

    int tribonacci(int _n) { // 定义函数 tribonacci，参数为 _n
        ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 输入输出加速
        n = _n; // 将 _n 赋值给成员变量 n
        solve(); // 调用 solve 函数进行计算
        return ret; // 返回结果 ret
    }
};

递归

class Solution {
public:
    int tribonacci(int i) { // 定义函数 tribonacci，参数为整数 i
        if (i == 0) return 0; // 如果 i 等于 0，返回 0
        if (i == 1) return 1; // 如果 i 等于 1，返回 1
        if (i == 2) return 1; // 如果 i 等于 2，返回 1
        if (i == 3) return 2; // 如果 i 等于 3，返回 2
        // 否则递归计算 i-1, i-2 和 i-3 位置的 tribonacci 值，并返回三者之和
        return tribonacci(i-1) + tribonacci(i-2) + tribonacci(i-3);
    }
};

面试题 08.01. 三步问题

三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

示例1:

输入：n = 3 输出：4 说明: 有四种走法 示例2:

输入：n = 5 输出：13 提示:

n范围在[1, 1000000]之间

状态表示,$dp[i]$表示上第$i$阶台阶有多少种上楼梯的方式.

状态转移方程,$dp[i]=dp[i-1]+dp[i-2]+dp[i-3]$.

填表顺序,从小到大,填写$i$位置状态需要用到$i-1,i-2,i-3$位置的状态.

初始化,特判,$dp[1]=1,dp[2]=2,dp[3]=4$.

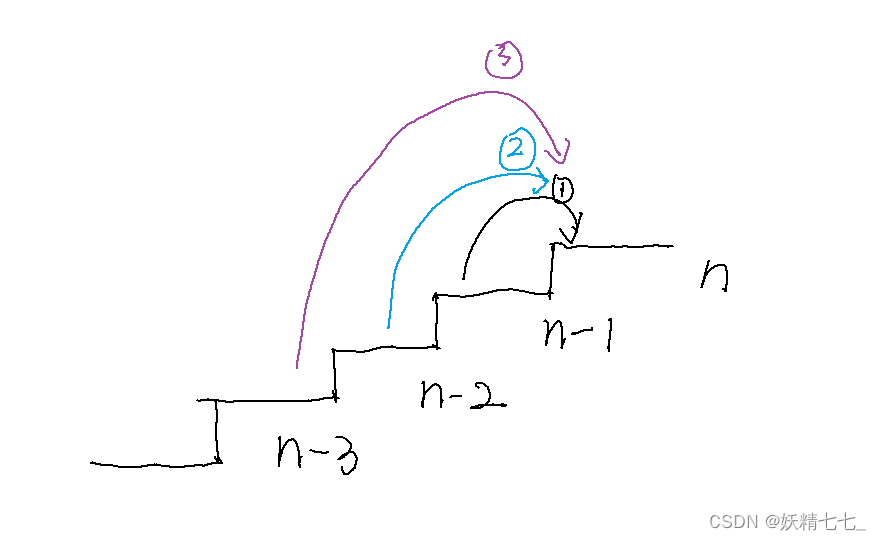
到达第$n$阶台阶,要么从$n-1$阶台阶向上走一步,要么从$n-2$阶台阶向上走两步,要么从$n-3$阶台阶向上走三步.
到达第$n$阶台阶的方法数等于到达第$n-1$阶台阶的方法数加上到达第$n-2$阶台阶的方法数加上到达第$n-3$阶台阶的方法数.

6.
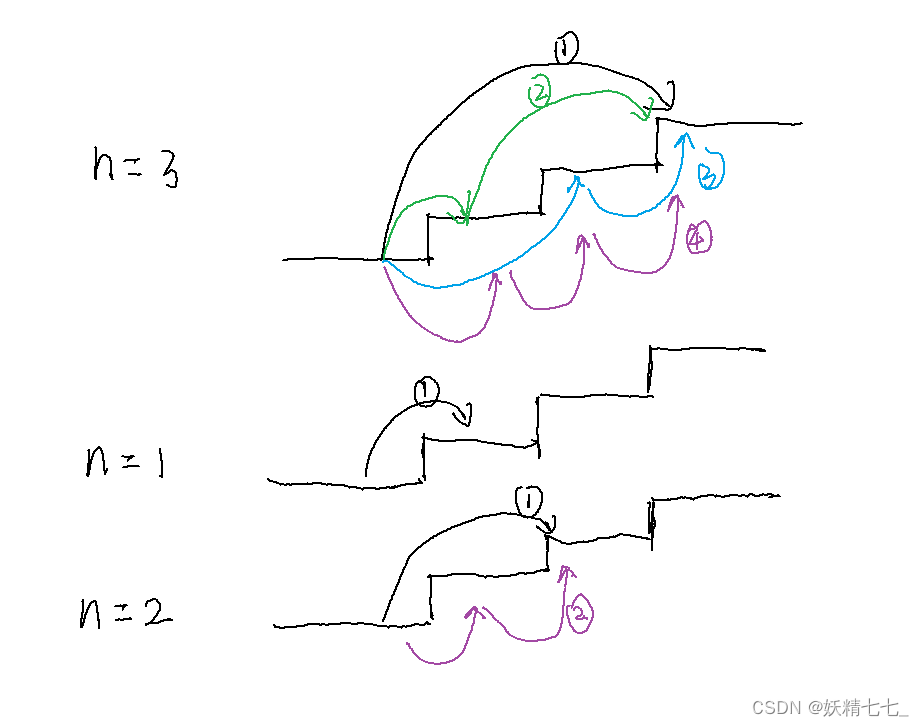
特判第一阶台阶,第二阶台阶,第三阶台阶.

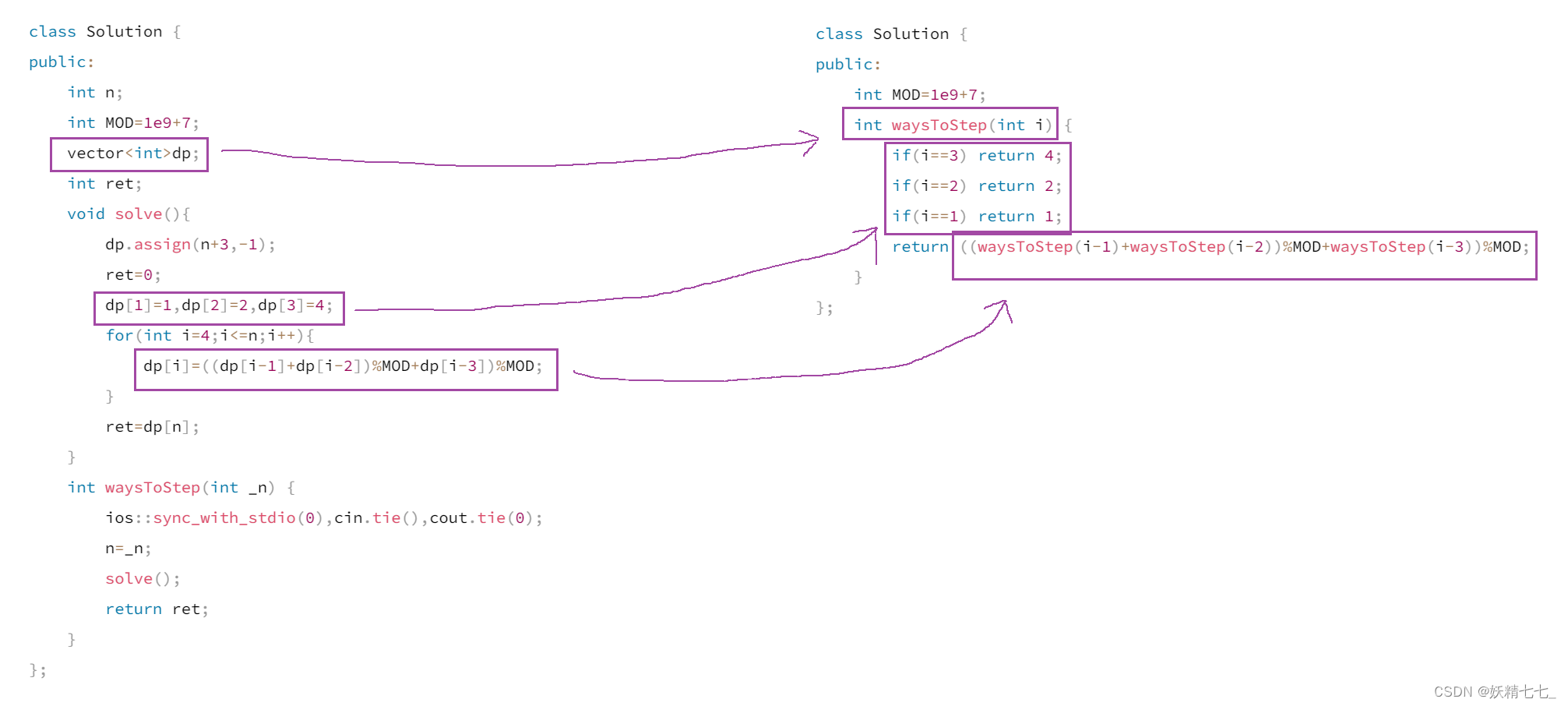
动态规划

class Solution {
public:
    int n; // 定义一个整数 n，用于存储目标的索引
    vector<int> dp; // 定义一个整型向量 dp，用于存储中间计算结果
    int ret; // 定义一个整数 ret，用于存储最终的结果
    void solve(){ // 定义一个求解函数 solve
        dp.assign(n+3, -1); // 初始化 dp 向量，大小为 n+3，初始值均为 -1
        ret = -1; // 初始化 ret 为 -1
        dp[0] = 0, dp[1] = 1, dp[2] = 1; // 初始化 dp 的前三个元素，分别为 0，1，1
        for (int i = 3; i <= n; i++) { // 从第 3 个元素开始，计算到第 n 个元素
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3]; // 三数相加，得到当前元素的值
        }
        ret = dp[n]; // 最终结果赋值给 ret
    }

    int tribonacci(int _n) { // 定义函数 tribonacci，参数为 _n
        ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 输入输出加速
        n = _n; // 将 _n 赋值给成员变量 n
        solve(); // 调用 solve 函数进行计算
        return ret; // 返回结果 ret
    }
};

递归

class Solution {
public:
    int MOD=1e9+7; // 定义常量 MOD，值为 1e9+7，用于取模运算
    int waysToStep(int i) { // 定义函数 waysToStep，参数为整数 i
        if (i == 3) return 4; // 如果 i 等于 3，返回 4
        if (i == 2) return 2; // 如果 i 等于 2，返回 2
        if (i == 1) return 1; // 如果 i 等于 1，返回 1
        // 否则递归计算 i-1, i-2 和 i-3 位置的 waysToStep 值，并进行取模运算后返回结果
        return ((waysToStep(i-1) + waysToStep(i-2)) % MOD + waysToStep(i-3)) % MOD;
    }
};

使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i
个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20] 输出：15 解释：你将从下标为 1 的台阶开始。

• 支付 15 ，向上爬两个台阶，到达楼梯顶部。 总花费为 15 。 示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1] 输出：6 解释：你将从下标为 0 的台阶开始。

• 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
• 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
• 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
• 支付 1 ，向上爬一个台阶，到达楼梯顶部。 总花费为 6 。

提示：

2 <= cost.length <= 1000 0 <= cost[i] <= 999

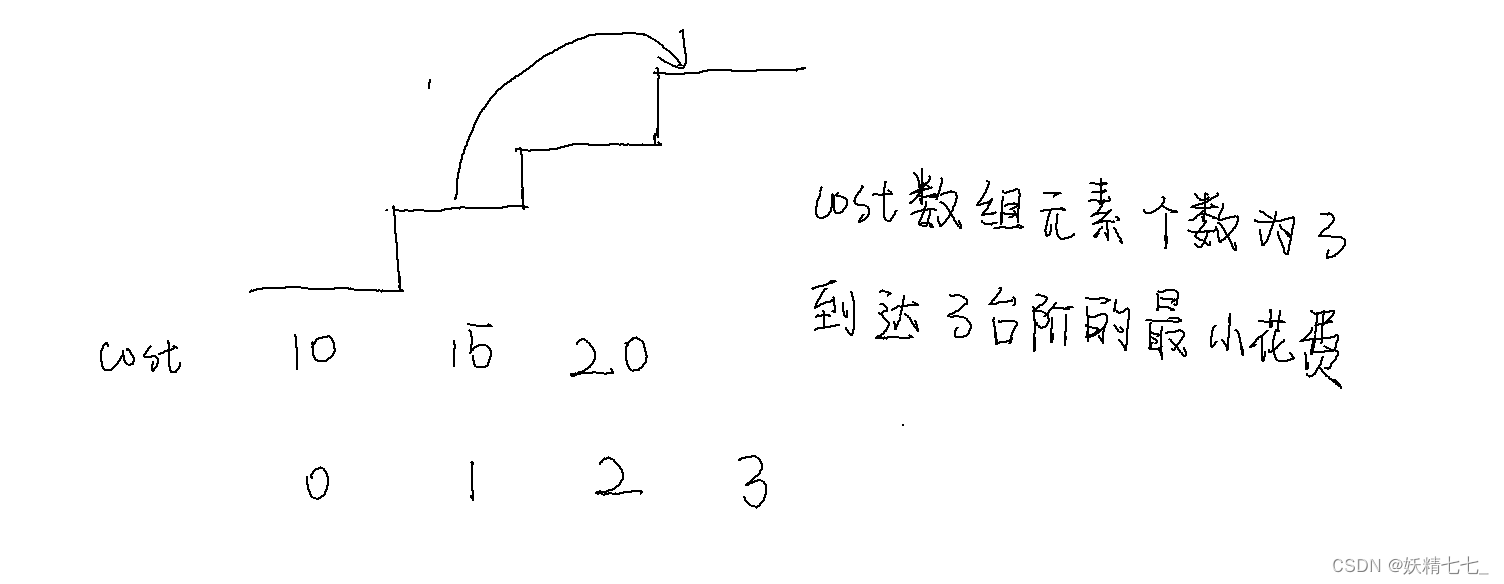
状态表示,$dp[i]$表示从最开始爬到第$i$个台阶花费的最小费用.

状态转移方程,$dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])$.

填表顺序,从小到大,填写$i$位置的状态需要用到$i-1,i-2,i-3$位置的状态.

初始化,特判,$dp[0]==dp[1]==0$.

动态规划

class Solution {
public:
    vector<int> cost; // 定义一个整型向量 cost，用于存储每一级台阶的花费
    int ret; // 定义一个整数 ret，用于存储最终的结果
    vector<int> dp; // 定义一个整型向量 dp，用于存储动态规划的中间结果
    void solve(){ // 定义一个求解函数 solve
        ret = 0; // 初始化 ret 为 0
        dp.assign(cost.size() + 1, -1); // 初始化 dp 向量，大小为 cost.size() + 1，初始值均为 -1
        dp[0] = 0, dp[1] = 0; // 初始化 dp 的前两个元素，均为 0
        for (int i = 2; i <= dp.size() - 1; i++) { // 从第 2 个元素开始，计算到第 dp.size() - 1 个元素
            // 当前元素的值为前一个元素加前一个台阶的花费和前两个元素加前两个台阶的花费的较小值
            dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);
        }
        ret = dp[dp.size() - 1]; // 最终结果赋值给 ret
    }
    int minCostClimbingStairs(vector<int>& _cost) { // 定义函数 minCostClimbingStairs，参数为整型向量 _cost
        ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 输入输出加速
        cost = _cost; // 将 _cost 赋值给成员变量 cost
        solve(); // 调用 solve 函数进行计算
        return ret; // 返回结果 ret
    }
};

递归

class Solution {
public:
    vector<int> arr; // 定义一个整型向量 arr，用于存储每一级台阶的花费

    int dfs(int i){ // 定义一个深度优先搜索函数 dfs，参数为整数 i
        if (i == 0) return 0; // 如果 i 等于 0，返回 0
        if (i == 1) return 0; // 如果 i 等于 1，返回 0

        // 否则递归计算前一个台阶和前两个台阶的最小花费
        return min(dfs(i-1) + arr[i-1], dfs(i-2) + arr[i-2]);
    }

    int minCostClimbingStairs(vector<int>& cost) { // 定义函数 minCostClimbingStairs，参数为整型向量 cost
        arr = cost; // 将 cost 赋值给成员变量 arr
        return dfs(arr.size()); // 调用 dfs 函数，传入台阶的总数，并返回结果
    }
};

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。
同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。
谢谢您的支持，期待与您在下一篇文章中再次相遇！