深度学习（一）

最新推荐文章于 2024-10-28 16:11:34 发布

是shallow吖

最新推荐文章于 2024-10-28 16:11:34 发布

阅读量214

点赞数

分类专栏：深度学习文章标签：深度学习人工智能

本文链接：https://blog.csdn.net/m0_74347510/article/details/132884066

版权

深度学习专栏收录该内容

2 篇文章

订阅专栏

本文介绍了深度学习的基本流程，包括数据预处理、模型构建（涉及损失函数、隐藏层、激活函数等）、训练与验证（训练集、开发集、过拟合预防）、测试和推理，以及关键概念如梯度清零、计算图、Mini-Batch和超参数调整。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

深度学习基本流程

数据集

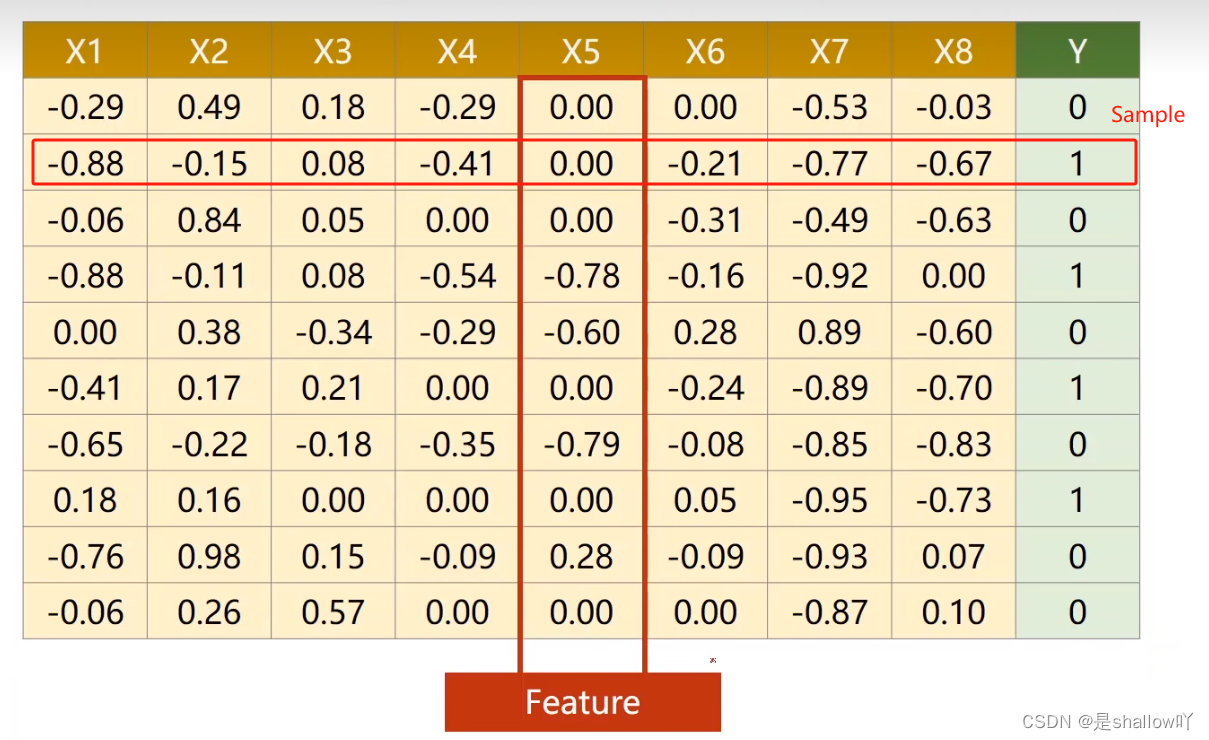
模型

评估模型靠的是损失函数，平均损失越低，模型越好

真实模型一定有损失

目标就是使损失尽可能的小，如何使损失最小

常见损失函数

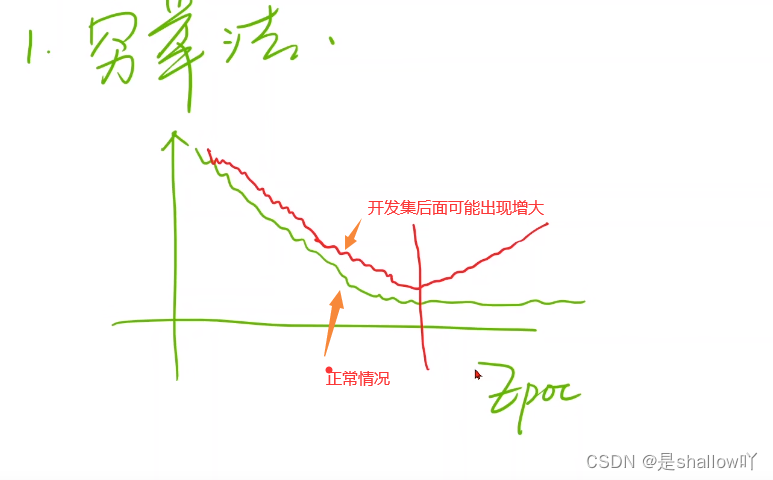
损失函数图像，横坐标一般是训练轮数

深度学习过程中要存盘，以免训练一半程序崩溃

可视化工具Visdom

MSE：（平均平方误差）

训练

训练又可以分为训练集和开发集，开发集就是测试集，使得模型有更好的泛化能力

训练过好容易出现过拟合，要提供泛化能力

测试

测试可以看到x，y用来测试模型是否好用

推理

线性回归

神经网络

隐藏层：

在一个神经网络中，当你使用监督学习训练它的时候，训练集包含了输入𝑥 也包含了目标输出 𝑦 ，所以术语隐藏层的含义是在训练集中，这些中间结点的准确值我们是不知道到的，也就是说你看不见它们在训练集中应具有的值。你能看见输入的值，你也能看见输出的值，但是隐藏层中的东西，在训练集中你是无法看到的。所以这也解释了词语隐藏层，只是表示你无法在训练集中看到他们。

这里的隐藏层将拥有两个参数𝑊 和 𝑏 ，给它们加上上标 [1] ( 𝑊 [1] , 𝑏 [1] ) ，表示这些参数是和第一层这个隐藏层有关系的。之后在这个例子中会看到𝑊 是一个 4x3 的矩阵，而 𝑏 是一个 4x1 的向量，第一个数字 4 源自于我们有四个结点或隐藏层单元，然后数字 3 源自于这里有三个输入特征，我们之后会更加详细地讨论这些矩阵的维数，到那时可能就更加清楚了。

隐藏层计算，在代码中实际上W就是个4x3的矩阵，B就是4x1的矩阵。

self.linear = torch.nn.Linear(3, 4) #3表示三个输入，因为第一层有四个神经元，所以输出是4
self.linear = torch.nn.Linear(4, 1)

函数内部实现如图所示

注：在编程过程中Wx需要转置

激活函数

Q:为什么需要激活函数？

A:引入非线性性：如果没有激活函数，整个神经网络就会变成一个线性模型，无法学习复杂的非线性关系。激活函数引入了非线性，使得神经网络能够逼近各种复杂的函数。

使用一个神经网络时，需要决定使用哪种激活函数用隐藏层上，哪种用在输出节点上。

这有一些选择激活函数的经验法则：

如果输出是 0 、 1 值（二分类问题），则输出层选择 sigmoid 函数，然后其它的所有单

元都选择 Relu 函数。这是很多激活函数的默认选择，如果在隐藏层上不确定使用哪个激活函数，那么通常会使用 Relu 激活函数。有时，也会使用 tanh 激活函数，但 Relu 的一个优点是：当 𝑧 是负值的时候，导数等于 0 。

sigmoid 函数： $f(x) = \frac{1}{1 + e^{-x}}$

在讨论优化算法时，有一点要说明：基本已经不用 sigmoid 激活函数了， tanh 函数在

所有场合都优于 sigmoid 函数。

但有一个例外：在二分类的问题中，对于输出层，因为 𝑦 的值是 0 或 1，所以想让ŷ 的数值介于 0 和 1 之间，而不是在 -1 和 +1 之间。所以需要使用 sigmoid 激活函数。

随机初始化

当你训练神经网络时,权重随机初始化是很重要的。对于逻辑回归，把权重初始化为0当然也是可以的。但是对于一个神经网络，如果你把权重或者参数都初始化为0那么梯度下降将不会起作用。

这个问题的解决方法就是随机初始化参数。你应该这么做：把[1]np.random.randn(2,2)(生成高斯分布)，通常再乘上一个小的数，比如 0.01（我们希望它们是随机的，但又不能太大，以免在前向传播时产生过大的值，从而导致激活函数饱和，这可能会降低网络的学习速度。），这样把它初始化为很小的随机数。然后没有这个对称的问题（叫做symmetry breaking problem），所以可以把初始化为 0，因为只要随机初始化你就有不同的隐含单元计算不同的东西，因此不会有 symmetry breaking 问题了。相似的，对于[2]你可以随机初始化，[2]可以初始化为 0。

深层神经网络（Deep L-layer neural network）

Q：为什么使用深层？举个例子理解。

A：深度模型可以从数据中学习到多层次、抽象的特征表达。通过逐层的计算，每一层可以将前一层的输出作为输入，进而学习到更高级别的特征，使模型能够从数据中提取更加复杂的信息。

例子：

首先，深度网络在计算的过程中，每一层可以看作是对图像的不同抽象层次的表示，从较低级的特征（如边缘）逐步到更高级的特征（如面部部位）。

举个例子，假设我们要建立一个人脸识别系统。当我们输入一张脸部的照片时，深度神经网络的第一层可以被视作一个特征探测器或边缘探测器。每个隐藏单元（神经元）在图像中会寻找特定方向的边缘，比如竖直方向或水平方向的边缘。

然后，第二层将会进一步组合这些边缘特征，比如将一些竖直边缘和水平边缘结合起来，以便检测到眼睛、鼻子等面部部位。

接着，更高层次的层将会将这些面部部位的特征结合在一起，识别出不同人脸的整体特征。

总的来说，深度网络的前几层可以被看作是探测简单的特征，如边缘，然后将它们结合起来，从而学习到更复杂的函数。这种层级化的处理方式也可以应用于图像以外的其他数据，比如语音识别。

Q:为什么需要计算图？

A:线性神经网络规模庞大且复杂，因此不好做梯度计算直接计算结果，因此引入了计算图

计算图：实现自动求导的基础。通过构建计算图，系统可以跟踪每个变量的计算历史，从而能够计算出相对于某个变量的导数（梯度）。这使得在训练神经网络时，可以自动地计算和更新模型参数，以最小化损失函数。

Q:为什么需要激活函数

A:激活函数引入了非线性变换，这对于模型的表达能力非常重要。如果没有激活函数，多层神经网络将仅仅是一系列线性变换的叠加，无法表示复杂的非线性关系。激活函数一般指的是sigomid函数

反向传播过程：

从输出层开始，计算损失对于网络中每个参数的梯度（导数）。
使用链式法则，将梯度从输出层逐层向后传播，更新每一层的参数。

Q:为什么要梯度清零

梯度累积：在训练过程中，梯度是累积的。如果不清零，每个迭代的梯度将会累积到之前的梯度中，导致更新的方向和幅度不受控制。
防止梯度爆炸：在深度神经网络中，梯度可能会变得非常大，导致参数更新过大，从而使模型的表现变得不稳定。通过清零梯度，可以避免这种情况。

Loss值必须是一个标量，所以当Loss值不为标量时，需要求和

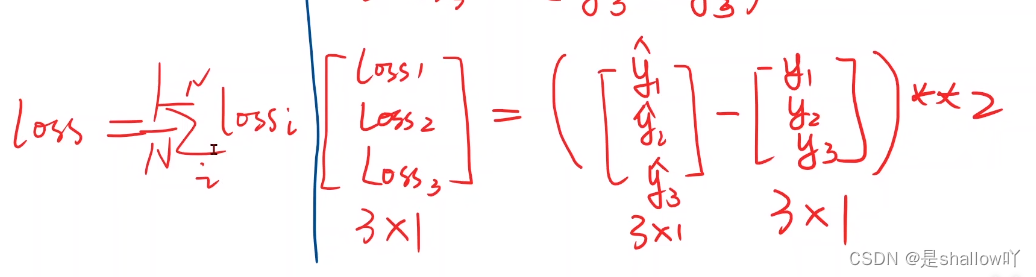
处理多维特征的输入

多维度数据集：

此时只要将线性模型改一下：

import numpy as np
import torch
"""model"""
class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid() # 这是一个模块，一个层

    def forward(self, x):
        x = self.sigmoid(self.linear1(x)) # 比较好的写法
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x

model = LinearModel()
"""构建加载数据集"""
"""dilimiter表示以，为分隔符， dtype表示数据类型，float32一般够用，double类型需要更高配置的显卡"""
xy = np.loadtxt('dataset/diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1]) # 用于将一个NumPy数组（numpy.ndarray）转换为对应的PyTorch张量（torch.Tensor）
y_data = torch.from_numpy(xy[:, [-1]]) # xy[:, [-1]]结果将是一个二维数组，其中包含了 xy 中所有行的最后一个元素。xy[:, -1]这将返回一个一维数组，其中包含了 xy 中所有行的最后一个元素。
print('x_data:', x_data) #.size()可以查看形状
print('y_data', y_data)
criterion = torch.nn.BCELoss(reduction='mean') # size_average=True已被移除
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print('epoch', epoch, ' loss:', loss.item())

    optimizer.zero_grad()
    loss.backward()

    optimizer.step()

Mini-Batch的使用

Q：为什么需要使用Mini-Batch？

A:

避免陷入局部极小值：

在深度学习中，模型的损失函数通常是非凸的，可能存在许多局部极小值。Mini-Batch 通过在每一步更新中引入一些随机性，可以使模型跳出局部极小值点，更有可能找到全局最优解。

减少训练时间：

使用 Mini-Batch 允许模型在每个训练步骤中只考虑一部分样本，从而减少了每个训练步骤的计算开销，加速了训练过程。

内存效率：

训练神经网络需要大量的数据，而且现实中的数据集可能非常大，无法一次性加载到内存中。使用 Mini-Batch 可以将数据集分成小块，每次只加载一小部分样本，从而节省内存空间。

import torch
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader


# prepare dataset
class DiabetesDataset(Dataset):
    def __init__(self, filepath):
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
        self.input = torch.from_numpy(xy[:, :-1])
        self.label = torch.from_numpy(xy[:, [-1]])
        self.len = xy.shape[0]  # xy.shape[0]表示第一个维度的大小，xy.shape[1]表示第二个维度的大小

    def __getitem__(self, item):
        return self.input[item], self.label[item]

    def __len__(self):
        return self.len


dataset = DiabetesDataset('dataset/diabetes.csv.gz')
train_loader = DataLoader(dataset=dataset, batch_size=16, shuffle=True, num_workers=0)  # num_workers 多线程


# design model using class
class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid() # 这是一个模块，一个层

    def forward(self, x):
        x = self.sigmoid(self.linear1(x)) # 比较好的写法
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x


model = LinearModel()

# construct loss and optimizer
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

for epoch in range(100):
    for i, data in enumerate(train_loader, 0): # enumerate(dataset, 0) 表示对 dataset 进行枚举操作，同时设置起始索引为 0。
        input, label = data
        label_pred = model(input)
        loss = criterion(label_pred, label)
        print(epoch, i, loss.item())

        optimizer.zero_grad()
        loss.backward()

        optimizer.step()

参数VS超参数

经验规律：经常试试不同的超参数，勤于检查结果，看看有没有更好的超参数取值，你将会得到设定超参数的直觉。

题外话：

函数传递未知个数的参数时，可以如此定义

def func(*args, **kwargs):#args为元组，kwargs为字典
    pass

func(1, 2, 3, 4, x=3, y=5)

线性回归代码示例：

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

X = torch.tensor([[1.0], [2.0], [3.0]])# 列代表特征个数，行代表数据个数
Y = torch.tensor([[2.5], [4.5], [6.5]])

class LinearModel(torch.nn.Module):
    """为什么没有backward？
       因为 torch.nn.Module 中已经提供了自动求导的功能
    """
    def __init__(self):
        super(LinearModel, self).__init__() #调用父类的构造
        self.linear = torch.nn.Linear(1, 1) #创建一个对象，这里的 (2, 1) 表示了输入特征的维度和输出特征的维度
        """线性单元实际上为y = x*w + b，但一般书写时是y = w^t*x + b， 所以要做个转置
           如果你将一个大小为 (batch_size, 2) 的张量传递给这个线性层，
           它将返回一个大小为 (batch_size, 1) 的张量。
           知道输入和输出，权重是自动计算维度的
        """
        
    def forward(self, x):
        y_pred = self.linear(x) #可调用对象，也继承至Module，因此也可以实现自动求导，此处实现y = x*w + b
        return y_pred


model = LinearModel()

#构造损失函数和优化器
criterion = torch.nn.MSELoss(size_average=False)#也继承至nn.Module，因此也会构建计算图，此处不求均值
"""reduce = True 表示是否求和降维"""
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)# model.parameters() 返回了神经网络模型中所有需要训练的参数（比如权重和偏置）的迭代器。

for epoch in range(1000):
    """前馈"""
    y_pred = model(X)
    loss = criterion(y_pred, Y)
    print(epoch, loss)#loss调用__str__函数，所以不会计算梯度
    
    optimizer.zero_grad()#梯度清零
    """反馈"""
    loss.backward()
    """更新"""
    optimizer.step()
    
print('w=', model.linear.weight.item())
print('b=', model.linear.bias.item())

# 测试
x_text = torch.Tensor([[4.0]])
y_text = model(x_text)
print('y_pred = ', y_text.data)

逻辑回归（二分类）

类别特征，不能简单用线性回归的输出值来做大小比较

Logistic Function: $f(x) = \frac{1}{1 + e^{-x}}$

在分类问题中使用 Logistic 函数的主要原因是它可以将输入的实数映射到一个在 0 到 1 之间的概率值，这正好符合了概率的定义。

Sigmoid functions：饱和函数，导数图像类似正态分布

交叉熵损失函数： $J(\theta) = - \frac{1}{m} \sum_{i=1}^{m} \left( y^{(i)} \log(\hat{y}^{(i)}) + (1-y^{(i)}) \log(1-\hat{y}^{(i)}) \right)$

反映的是两个概率的差异程度

二分类实现（此代码中使用的是线性回归，因此数据应该是有单调的特性）：

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
import torch.nn.functional as F

x_data = torch.Tensor([[1.0], [2.0], [3.0], [4.0], [5.0], [6.0]])
y_data = torch.Tensor([[0], [0], [0], [1], [1], [1]])

class LogisticRegressionModel(torch.nn.Module):
    """为什么没有backward？
       因为 torch.nn.Module 中已经提供了自动求导的功能
    """
    def __init__(self):
        super(LogisticRegressionModel, self).__init__() #调用父类的构造
        self.linear = torch.nn.Linear(1, 1) #创建一个对象，这里的 (2, 1) 表示了输入特征的维度和输出特征的维度
        """线性单元实际上为y = x*w + b，但一般书写时是y = w^t*x + b， 所以要做个转置
           如果你将一个大小为 (batch_size, 2) 的张量传递给这个线性层，
           它将返回一个大小为 (batch_size, 1) 的张量。
           知道输入和输出，权重是自动计算维度的
        """
        
    def forward(self, x):
        """F.sigmoid(self.linear(x))会引发warning，此处更改为torch.sigmoid(self.linear(x))
        torch.nn.Sigmoid() 在模型中作为一个层来使用，可以包含在神经网络的结构中，而不是对单个张量进行操作。
        torch.sigmoid() 是一个数学函数，它接受一个张量作为输入，并返回元素级别的Sigmoid函数的计算结果。
        """
        y_pred = F.sigmoid(self.linear(x)) #使分布在0，1之间
        return y_pred
model = LogisticRegressionModel()

criterion = torch.nn.BCELoss(size_average = False) #交叉熵损失
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

# 测试
x_text = torch.Tensor([[3.0]])
y_text = model(x_text)
print('y_pred = ', y_text.data)

多分类问题：