一、大气运动的基本特征
前言
本课程使用教材为《天气学原理和方法(第四版)》(气象出版社),文章根据课堂笔记和教材内容整理订正编写,文章内容如有错误,请指正。
系列文章链接如下:
大气运动基本特征
气团与锋
气旋与反气旋
天气形势与天气要素预报
大气环流
文章目录
旋转坐标系中的真实力
气压梯度力
气压梯度存在形成气压梯度力,促使大气运动
使用立方体气块模型分三个方向分析,单位质量气块受到的净压力称为气压梯度力,用矢量表示为
G
⃗
=
−
1
ρ
∇
p
\vec{G}=-\frac{1}{\rho} \nabla p
G=−ρ1∇p
其中
−
∇
p
- \nabla p
−∇p 表示气压梯度力是由高压指向低压
地心引力
根据牛顿万有引力公式的矢量形式得到
F
⃗
=
−
G
M
m
r
2
⋅
r
⃗
r
\vec{F} = - \frac{GMm}{r^2} \cdot \frac{\vec{r}}{r}
F=−r2GMm⋅rr
摩擦力
流体摩擦力理解为单位质量流体所受到的净粘滞力
从微观上看,粘滞力的产生是由于分子无规则运动引起的动量交换
粘滞力与风速垂直切变成正比
假设大气沿着
x
x
x 正方向运动且速度
u
u
u 随高度增加而增加
f
z
x
=
μ
A
∂
u
∂
z
=
A
τ
z
x
f_{zx} = \mu A \frac{\partial u}{\partial z} = A \tau_{zx}
fzx=μA∂z∂u=Aτzx
其中
A
A
A 为面积,去除面积可得到单位面积的切应力
τ
z
x
\tau_{zx}
τzx
对于一个空气块,若速度 u u u 随高度线性变化,根据以上公式得气块上界面与下界面的粘滞力抵消,净粘滞力为0
由此可得摩擦力主要是由风在垂直方向上非线性变化引起,而对于实际问题,水平方向上的非线性变化可以忽略,因此可做近似
F
⃗
=
μ
ρ
∇
2
V
⃗
≈
ν
(
∂
2
u
∂
z
2
i
⃗
+
∂
2
v
∂
z
2
j
⃗
+
∂
2
w
∂
z
2
k
⃗
)
\vec{F} = \frac{\mu}{\rho} \nabla ^2 \vec{V} \approx \nu(\frac{\partial ^2 u}{\partial z^2} \vec{i}+\frac{\partial ^2 v}{\partial z^2} \vec{j}+\frac{\partial ^2 w}{\partial z^2} \vec{k})
F=ρμ∇2V≈ν(∂z2∂2ui+∂z2∂2vj+∂z2∂2wk)
旋转坐标系中的非真实力
惯性离心力
物体旋转时的向心加速度为
d
V
⃗
d
t
=
−
Ω
2
R
⃗
\frac{d\vec{V}}{dt} = - \Omega ^2 \vec{R}
dtdV=−Ω2R
可得到旋转坐标系下的惯性离心力(Centrifugal Force)
C
⃗
=
Ω
2
R
⃗
\vec{C} = \Omega^2 \vec{R}
C=Ω2R
重力
将地心引力与惯性离心力矢量相加可得到重力,地球为椭球体,重力垂直于地球表面
地转偏向力
物体在旋转坐标系中运动发生偏向,为了描述这样的偏向,在旋转坐标系中引入地转偏向力
设有一物体在地球纬度为
ϕ
\phi
ϕ 的位置
A
⃗
=
−
2
Ω
⃗
×
V
⃗
=
−
2
∣
i
⃗
j
⃗
k
⃗
0
Ω
cos
ϕ
Ω
sin
ϕ
u
v
w
∣
\vec{A} = -2 \vec{\Omega } \times \vec{V}=-2 \left | \begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ 0 & \Omega \cos \phi & \Omega \sin \phi \\ u & v & w \\ \end{matrix} \right |
A=−2Ω×V=−2
i0ujΩcosϕvkΩsinϕw
定义
f
=
2
Ω
sin
ϕ
f= 2 \Omega \sin \phi
f=2Ωsinϕ
用于计算水平方向地转偏向力
推导:动力气象学角动量守恒方法
设北半球中纬度某地区有一西风,风速为 u ⃗ \vec{u} u,可得该空气块角动量
L ⃗ = R ⃗ × ( u ⃗ + Ω × R ⃗ ) \vec{L} = \vec{R} \times ( \vec{u} + \Omega \times \vec{R}) L=R×(u+Ω×R)
若此时该向东运动的空气块受到一定的扰动,使其向南北偏移或向上偏移无穷小量,使得垂直地轴半径变为 R + δ R R+\delta R R+δR
( R ⃗ + δ R ⃗ ) × ( u ⃗ + δ u ⃗ ) + ( R ⃗ + δ R ⃗ ) × Ω ⃗ × ( R ⃗ + δ R ⃗ ) = R ⃗ × ( u ⃗ + Ω ⃗ × R ⃗ ) (\vec{R} + \delta \vec{R}) \times (\vec{u}+\delta \vec{u}) + (\vec{R} + \delta \vec{R}) \times \vec{\Omega} \times (\vec{R} +\delta \vec{R}) = \vec{R} \times (\vec{u} + \vec{\Omega} \times \vec{R}) (R+δR)×(u+δu)+(R+δR)×Ω×(R+δR)=R×(u+Ω×R)
假设初始 u = 0 u=0 u=0,对方程化简可得
Ω R 2 = ( Ω + δ u R + δ R ) ( R + δ R ) 2 \Omega R^2 = (\Omega + \frac{\delta u}{R+\delta R})(R+\delta R)^2 ΩR2=(Ω+R+δRδu)(R+δR)2
解此方程并忽略高阶无穷小得到
δ u = − 2 Ω δ R \delta u = -2\Omega \delta R δu=−2ΩδR
设该点纬度为 ϕ \phi ϕ
δ R = δ z cos ϕ − δ y sin ϕ \delta R = \delta z \cos \phi - \delta y\sin \phi δR=δzcosϕ−δysinϕ
代入得到地转偏向力 x x x 方向分量
δ u = − 2 Ω ( δ z cos ϕ − δ y sin ϕ ) \delta u = -2 \Omega (\delta z \cos \phi - \delta y \sin \phi) δu=−2Ω(δzcosϕ−δysinϕ)
d u d t = − 2 Ω ( w cos ϕ − v sin ϕ ) \frac{du}{dt} = -2 \Omega (w \cos \phi - v \sin \phi) dtdu=−2Ω(wcosϕ−vsinϕ)
当有相对运动 u u u 时,惯性离心力表达式
C ⃗ = ( Ω + u R ) 2 R ⃗ \vec{C} = (\Omega +\frac{u}{R})^2 \vec{R} C=(Ω+Ru)2R
展开忽略高阶无穷小(即第三项)可得
C ⃗ ≈ Ω 2 R ⃗ + 2 Ω u R ⃗ R \vec{C} \approx \Omega ^2 \vec{R} + 2 \Omega u \frac{\vec{R}}{R} C≈Ω2R+2ΩuRR
与没有相对运动时相比,增加的一部分惯性离心力表现为地转偏向力,可得到另外两个分量
d w d t = 2 Ω u cos ϕ \frac{dw}{dt} = 2\Omega u \cos \phi dtdw=2Ωucosϕ
d v d t = − 2 Ω u sin ϕ \frac{dv}{dt} = -2 \Omega u \sin \phi dtdv=−2Ωusinϕ
综上可得最终矢量表达式
大尺度大气运动是准水平的,垂直方向上运动速度很小(比水平方向少 1 0 2 10^{2} 102 量级)可以忽略
球坐标系与局地直角坐标系的坐标变换
设地球中纬度有一点,经纬度位置为
(
λ
,
ϕ
)
(\lambda , \phi)
(λ,ϕ), 地球半径为
r
r
r,在该点建立局地直角坐标系,向东为
x
x
x 正方向,向北为
y
y
y 正方向,垂直地表为
z
z
z 正方向,可得
{
d
x
=
r
cos
ϕ
d
λ
d
y
=
r
d
ϕ
d
z
=
d
r
\begin{cases} dx = r \cos \phi d \lambda \\ dy = r d \phi \\ dz = dr \\ \end{cases}
⎩
⎨
⎧dx=rcosϕdλdy=rdϕdz=dr
控制大气运动的基本规律
局地导数和全导数的关系
根据Lagrange参考系和欧拉参考系关系
d
(
□
)
d
t
=
∂
(
□
)
∂
t
+
(
V
⃗
⋅
∇
)
(
□
)
\frac{d(\square)}{dt} = \frac{\partial (\square)}{\partial t} +(\vec{V} \cdot \nabla ) (\square)
dtd(□)=∂t∂(□)+(V⋅∇)(□)
移项可得
∂
(
□
)
∂
t
=
d
(
□
)
d
t
−
(
V
⃗
⋅
∇
)
(
□
)
\frac{\partial (\square)}{\partial t} = \frac{d(\square)}{dt} - (\vec{V} \cdot \nabla ) (\square)
∂t∂(□)=dtd(□)−(V⋅∇)(□)
其中括号内可以是很多物理量,物理量的局地变化由个体变化和平流变化组成
大气运动方程的矢量形式
d
V
⃗
d
t
=
−
1
ρ
∇
p
−
2
Ω
⃗
×
V
⃗
+
g
⃗
+
F
⃗
\frac{d\vec{V}}{dt} = -\frac{1}{\rho} \nabla p -2 \vec{\Omega} \times \vec{V} + \vec{g} + \vec{F}
dtdV=−ρ1∇p−2Ω×V+g+F
右式分别是气压梯度力、地转偏向力、重力、摩擦力
大气运动方程在局地直角坐标系中的形式
{ d u d t = − 1 ρ ∂ p ∂ x + 2 Ω ( v sin ϕ − w cos ϕ ) + F x d v d t = − 1 ρ ∂ p ∂ y − 2 Ω u sin ϕ + F y d w d t = − 1 ρ ∂ p ∂ z + 2 Ω u cos ϕ − g + F z \begin{cases} \frac{du}{dt} = -\frac{1}{\rho} \frac{\partial p}{\partial x} + 2\Omega(v\sin \phi -w\cos \phi ) + F_x\\ \frac{dv}{dt} = -\frac{1}{\rho} \frac{\partial p}{\partial y} -2\Omega u \sin \phi + F_y \\ \frac{dw}{dt} = -\frac{1}{\rho} \frac{\partial p}{\partial z} +2\Omega u \cos \phi -g + F_z \\ \end{cases} ⎩ ⎨ ⎧dtdu=−ρ1∂x∂p+2Ω(vsinϕ−wcosϕ)+Fxdtdv=−ρ1∂y∂p−2Ωusinϕ+Fydtdw=−ρ1∂z∂p+2Ωucosϕ−g+Fz
大气运动方程在球坐标系中的形式
首先矢量求导
d
V
⃗
d
t
=
d
u
d
t
i
⃗
+
d
v
d
t
j
⃗
+
d
w
d
t
k
⃗
+
u
d
i
⃗
d
t
+
v
d
j
⃗
d
t
+
w
d
k
⃗
d
t
\frac{d\vec{V}}{dt} = \frac{du}{dt} \vec{i} + \frac{dv}{dt} \vec{j} + \frac{dw}{dt} \vec{k} + u \frac{d\vec{i}}{dt} +v \frac{d\vec{j}}{dt} + w \frac{d\vec{k}}{dt}
dtdV=dtdui+dtdvj+dtdwk+udtdi+vdtdj+wdtdk
其中在球坐标系下
d
i
⃗
d
t
=
∂
i
⃗
∂
t
+
∂
i
⃗
∂
λ
d
λ
d
t
+
∂
i
⃗
∂
ϕ
d
ϕ
d
t
+
∂
i
⃗
∂
r
d
r
d
t
\frac{d\vec{i}}{dt} = \frac{\partial \vec{i}}{\partial t} +\frac{\partial \vec{i}}{\partial \lambda}\frac{d\lambda}{dt} +\frac{\partial \vec{i}}{\partial \phi}\frac{d\phi}{dt} +\frac{\partial \vec{i}}{\partial r}\frac{dr}{dt}
dtdi=∂t∂i+∂λ∂idtdλ+∂ϕ∂idtdϕ+∂r∂idtdr
其余方向同理,根据球面上的几何特征可得(画图分析)
∂
i
⃗
∂
ϕ
=
∂
i
⃗
∂
r
=
∂
j
⃗
∂
r
=
∂
k
⃗
∂
r
=
0
\frac{\partial \vec{i}}{\partial \phi} = \frac{\partial \vec{i}}{\partial r} = \frac{\partial \vec{j}}{\partial r} = \frac{\partial \vec{k}}{\partial r} = 0
∂ϕ∂i=∂r∂i=∂r∂j=∂r∂k=0
∂
i
⃗
∂
t
=
∂
i
⃗
∂
t
=
∂
i
⃗
∂
t
=
0
\frac{\partial \vec{i}}{\partial t} = \frac{\partial \vec{i}}{\partial t} = \frac{\partial \vec{i}}{\partial t} = 0
∂t∂i=∂t∂i=∂t∂i=0
根据坐标变换可得
{
d
i
⃗
d
t
=
u
r
cos
ϕ
∂
i
⃗
∂
λ
d
j
⃗
d
t
=
u
r
cos
ϕ
∂
j
⃗
∂
λ
+
v
r
∂
j
⃗
∂
ϕ
d
k
⃗
d
t
=
u
r
cos
ϕ
∂
k
⃗
∂
λ
+
v
r
∂
k
⃗
∂
ϕ
\begin{cases} \frac{d\vec{i}}{dt} = \frac{u}{r \cos \phi} \frac{\partial \vec{i}}{\partial \lambda} \\ \frac{d\vec{j}}{dt} = \frac{u}{r \cos \phi} \frac{\partial \vec{j}}{\partial \lambda} + \frac{v}{r} \frac{\partial \vec{j}}{\partial \phi} \\ \frac{d\vec{k}}{dt} = \frac{u}{r \cos \phi} \frac{\partial \vec{k}}{\partial \lambda} + \frac{v}{r} \frac{\partial \vec{k}}{\partial \phi} \\ \end{cases}
⎩
⎨
⎧dtdi=rcosϕu∂λ∂idtdj=rcosϕu∂λ∂j+rv∂ϕ∂jdtdk=rcosϕu∂λ∂k+rv∂ϕ∂k
在球面上根据几何关系及其弦和切线的近似可得
∂
i
⃗
∂
λ
=
j
⃗
sin
ϕ
−
k
⃗
cos
ϕ
\frac{\partial \vec{i}}{\partial \lambda} = \vec{j} \sin \phi - \vec{k} \cos \phi
∂λ∂i=jsinϕ−kcosϕ
∂
j
⃗
∂
λ
=
−
sin
ϕ
i
⃗
\frac{\partial \vec{j}}{\partial \lambda} = - \sin \phi \vec{i}
∂λ∂j=−sinϕi
∂
j
⃗
∂
ϕ
=
−
k
⃗
\frac{\partial \vec{j}}{\partial \phi} = - \vec{k}
∂ϕ∂j=−k
k
k
k 方向类似,代入上式可得球坐标系加速度分解
d
V
⃗
d
t
=
(
d
u
d
t
−
u
v
tan
ϕ
r
+
u
v
r
)
i
⃗
+
(
d
v
d
t
+
u
2
tan
ϕ
r
+
v
w
r
)
j
⃗
+
(
d
w
d
t
−
u
2
+
v
2
r
)
k
⃗
\frac{d\vec{V}}{dt} = (\frac{du}{dt} - \frac{uv \tan \phi}{r} + \frac{uv}{r}) \vec{i} +(\frac{dv}{dt} + \frac{u^2 \tan \phi}{r} + \frac{vw}{r}) \vec{j} + (\frac{dw}{dt} - \frac{u^2+v^2}{r}) \vec{k}
dtdV=(dtdu−ruvtanϕ+ruv)i+(dtdv+ru2tanϕ+rvw)j+(dtdw−ru2+v2)k
对气压梯度力进行分解
−
1
ρ
∇
p
=
−
1
ρ
(
∂
p
r
cos
ϕ
∂
λ
)
i
⃗
+
∂
p
r
∂
ϕ
j
⃗
+
∂
p
∂
r
k
⃗
-\frac{1}{\rho} \nabla p = -\frac{1}{\rho} (\frac{\partial p}{r \cos \phi \partial \lambda})\vec{i} + \frac{\partial p}{r\partial \phi} \vec{j} + \frac{\partial p}{\partial r} \vec{k}
−ρ1∇p=−ρ1(rcosϕ∂λ∂p)i+r∂ϕ∂pj+∂r∂pk
同理对地转偏向力和摩擦力分解,重力只在
k
k
k 方向有分量,最终得到球坐标系下大气运动方程
{
d
u
d
t
−
u
v
tan
ϕ
r
+
u
v
r
=
−
1
ρ
(
∂
p
r
cos
ϕ
∂
λ
)
+
2
Ω
v
sin
ϕ
−
2
Ω
w
cos
ϕ
+
F
λ
d
v
d
t
+
u
2
tan
ϕ
r
+
v
w
r
=
−
1
ρ
∂
p
r
∂
ϕ
−
2
Ω
u
sin
ϕ
+
F
ϕ
d
w
d
t
−
u
2
+
v
2
r
=
−
1
ρ
∂
p
∂
r
−
g
+
2
Ω
u
cos
ϕ
+
F
r
\begin{cases} \frac{du}{dt} - \frac{uv \tan \phi}{r} + \frac{uv}{r} = -\frac{1}{\rho} (\frac{\partial p}{r \cos \phi \partial \lambda}) + 2\Omega v \sin \phi - 2\Omega w \cos \phi +F_{\lambda} \\ \frac{dv}{dt} + \frac{u^2 \tan \phi}{r} + \frac{vw}{r} = -\frac{1}{\rho} \frac{\partial p}{r\partial \phi} -2\Omega u \sin \phi +F_{\phi} \\ \frac{dw}{dt} - \frac{u^2+v^2}{r} = - \frac{1}{\rho} \frac{\partial p}{\partial r}-g +2\Omega u \cos \phi + F_r \\ \end{cases}
⎩
⎨
⎧dtdu−ruvtanϕ+ruv=−ρ1(rcosϕ∂λ∂p)+2Ωvsinϕ−2Ωwcosϕ+Fλdtdv+ru2tanϕ+rvw=−ρ1r∂ϕ∂p−2Ωusinϕ+Fϕdtdw−ru2+v2=−ρ1∂r∂p−g+2Ωucosϕ+Fr
状态方程
对于单位质量理想气体
p
=
ρ
R
T
p = \rho RT
p=ρRT
质量守恒与连续方程
- Lagrange观点:
d ρ d t = − ρ ∇ ⋅ V ⃗ \frac{d\rho}{dt} = - \rho \nabla \cdot \vec{V} dtdρ=−ρ∇⋅V
其中 ∇ ⋅ V ⃗ \nabla \cdot \vec{V} ∇⋅V 为速度散度 - Eular观点:
∂ ρ ∂ t = − ∇ ⋅ ( ρ V ⃗ ) \frac{\partial \rho}{\partial t} = - \nabla \cdot (\rho \vec{V}) ∂t∂ρ=−∇⋅(ρV)
其中 ∇ ⋅ ρ V ⃗ \nabla \cdot \rho \vec{V} ∇⋅ρV 可以理解为质量散度
能量方程
机械能方程为球坐标系中运动方程分别乘上
u
,
v
,
w
u,v,w
u,v,w 得到
d
d
t
[
u
2
+
v
2
+
w
2
2
+
ϕ
]
=
−
1
ρ
V
⃗
⋅
∇
p
+
V
⃗
⋅
F
⃗
\frac{d}{dt}[\frac{u^2+v^2+w^2}{2} +\phi]= -\frac{1}{\rho} \vec{V} \cdot \nabla p + \vec{V} \cdot \vec{F}
dtd[2u2+v2+w2+ϕ]=−ρ1V⋅∇p+V⋅F
热力学第一定律
c
v
d
T
d
t
+
p
d
α
d
t
=
d
Q
d
t
c_v \frac{dT}{dt} + p \frac{d \alpha}{dt} = \frac{dQ}{dt}
cvdtdT+pdtdα=dtdQ
其中
α
\alpha
α 为单位质量对应的体积,即比体积
根据理想气体状态方程的微分形式,可以变形方程
c
p
d
T
d
t
−
α
d
p
d
t
=
d
Q
d
t
c_p \frac{dT}{dt} - \alpha \frac{dp}{dt} =\frac{dQ}{dt}
cpdtdT−αdtdp=dtdQ
反映了热能与机械能的转换,不同下垫面长波辐射不同,以及水汽潜热释放不同,大气获取的热量不同,因此会有不同的动能,使得大气运动。
绝热过程与位温
θ
T
=
(
1000
p
)
R
d
c
p
\frac{\theta }{T}=(\frac{1000}{p})^{\frac{R_d}{c_p}}
Tθ=(p1000)cpRd
其中
θ
\theta
θ 为位温,
R
d
R_d
Rd 为干空气气体常数
大气热力学稳定度
T
∂
θ
θ
∂
z
=
∂
T
∂
z
+
g
c
p
=
−
Γ
+
Γ
d
\frac{T\partial \theta}{\theta \partial z} = \frac{\partial T}{\partial z} + \frac{g}{c_p} =-\Gamma +\Gamma_d
θ∂zT∂θ=∂z∂T+cpg=−Γ+Γd
机械能方程与热力学第一定律结合得到总能量方程
d
Q
d
t
=
d
d
t
[
u
2
+
v
2
+
w
2
2
+
ϕ
+
c
v
T
+
p
α
]
−
α
∂
p
∂
t
−
V
⃗
⋅
F
⃗
\frac{dQ}{dt} = \frac{d}{dt}[\frac{u^2+v^2+w^2}{2} + \phi + c_vT +p\alpha] -\alpha \frac{\partial p}{\partial t} -\vec{V} \cdot \vec{F}
dtdQ=dtd[2u2+v2+w2+ϕ+cvT+pα]−α∂t∂p−V⋅F
大尺度运动系统的控制方程
尺度分析
针对不同类型的运动估计基本方程各项量级的一种简便方法
对基本方程进行简化,忽略小项,从而得到大尺度系统(一般空间尺度大于1000km为大尺度)控制方程
大尺度系统的性质:准定常,准水平、准静态,地转平衡、无辐散
中纬度大尺度系统常见特征值
L
∼
1
0
6
m
,
H
∼
1
0
4
m
,
V
(
u
,
v
)
∼
10
m
/
s
,
w
∼
1
0
−
2
m
/
s
,
t
∼
1
0
5
s
L \sim 10^6m,H \sim 10^4m,V(u,v) \sim 10 m/s, w \sim 10^{-2} m/s, t \sim 10^5 s
L∼106m,H∼104m,V(u,v)∼10m/s,w∼10−2m/s,t∼105s
自左向右分别为水平位移、地面到对流层顶的高度、水平风速、垂直风速、水平运动
L
L
L 所需要的时间
基本方程的简化
- 零级简化:保留方程中数量级最大的各项
- 一级简化:保留方程中数量级最大和比它小一个数量级的各项(注意不是指第二大)
例:对于垂直方向上的运动方程
d w d t = − 1 ρ ∂ p ∂ z + 2 Ω u cos ϕ − g + F z \frac{dw}{dt} = -\frac{1}{\rho} \frac{\partial p}{\partial z} +2\Omega u \cos \phi -g + F_z dtdw=−ρ1∂z∂p+2Ωucosϕ−g+Fz
数量级最大的项为 − 1 ρ ∂ p ∂ z , g -\frac{1}{\rho} \frac{\partial p}{\partial z},g −ρ1∂z∂p,g,由此可得到静力平衡方程
− 1 ρ ∂ p ∂ z − g = 0 -\frac{1}{\rho} \frac{\partial p}{\partial z} - g = 0 −ρ1∂z∂p−g=0
气压坐标系中的基本方程组
位势高度与海拔高度
位势:单位质量空气从海平面上升到高度z时克服重力做的功
ϕ
=
∫
0
z
g
d
z
\phi = \int^{z}_0 gdz
ϕ=∫0zgdz
假设重力加速度为
9.8
m
/
s
2
9.8 m/s^2
9.8m/s2 常量,根据位势可定义位势高度
H
=
1
9.8
∫
0
z
g
d
z
=
1
9.8
ϕ
H = \frac{1}{9.8} \int^{z}_0 g dz = \frac{1}{9.8} \phi
H=9.81∫0zgdz=9.81ϕ
单位为位势米
g
p
m
gpm
gpm,位势十米
10
g
p
m
10gpm
10gpm 或
d
a
g
p
m
dagpm
dagpm
因为不同地点重力加速度并不一定相等,因此某一地点,位势高度与海拔高度并不一定相等,但很接近,等位势面与地球表面平行(把地球看作是椭球)
气压坐标系与高度坐标系的转换
等压面上气压固定
d
p
=
∂
p
∂
x
d
x
+
∂
p
∂
y
d
y
+
∂
p
∂
z
d
z
=
0
dp = \frac{\partial p}{\partial x} dx + \frac{\partial p}{\partial y} dy + \frac{\partial p}{\partial z} dz = 0
dp=∂x∂pdx+∂y∂pdy+∂z∂pdz=0
再对高度
z
z
z 进行全微分
d
z
=
∂
z
∂
x
d
x
+
∂
z
∂
y
d
y
dz = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy
dz=∂x∂zdx+∂y∂zdy
将两个全微分结果联立,可得到
∂
p
∂
x
+
∂
p
∂
z
∂
z
∂
x
=
0
∂
p
∂
y
+
∂
p
∂
z
∂
z
∂
y
=
0
\begin{align*} \frac{\partial p}{\partial x} + \frac{\partial p}{\partial z}\frac{\partial z}{\partial x} = 0 \\ \frac{\partial p}{\partial y} + \frac{\partial p}{\partial z}\frac{\partial z}{\partial y} = 0 \\ \end{align*}
∂x∂p+∂z∂p∂x∂z=0∂y∂p+∂z∂p∂y∂z=0
结合静力方程(p坐标系使用的前提)
∂
p
∂
z
=
−
ρ
g
\frac{\partial p}{\partial z} = - \rho g
∂z∂p=−ρg
可得到气压梯度力为
−
1
ρ
∇
p
=
−
∇
ϕ
-\frac{1}{\rho} \nabla p = - \nabla \phi
−ρ1∇p=−∇ϕ
气压坐标系下的连续方程
∂
u
∂
x
+
∂
v
∂
y
+
∂
ω
∂
p
=
0
\frac{\partial u}{\partial x} + \frac{\partial v }{\partial y} +\frac{\partial \omega}{\partial p} = 0
∂x∂u+∂y∂v+∂p∂ω=0
其中
ω
=
∂
p
∂
t
\omega=\frac{\partial p}{\partial t}
ω=∂t∂p 为气压坐标系下垂直方向速度,向下运动为正
气压坐标系下的能量方程
∂
T
∂
t
+
V
h
⃗
⋅
∇
p
T
−
σ
p
ω
=
1
c
p
d
Q
d
t
\frac{\partial T}{\partial t} +\vec{V_h} \cdot \nabla_p T -\sigma_p \omega =\frac{1}{c_p} \frac{dQ}{dt}
∂t∂T+Vh⋅∇pT−σpω=cp1dtdQ
大气绝热,定常且稳定层结时,暖平流上升,冷平流下沉
风场与气压场的关系
自然坐标系
自然坐标为曲线坐标,一般水平轴方向会随时间和地点发生变化,自然坐标系分为两个方向,切向和法向
在自然坐标系下,北半球,气旋周围空气流动的曲率半径为正,反气旋为负,且得到 ∂ p ∂ n < 0 \frac{\partial p}{\partial n} < 0 ∂n∂p<0
自然坐标系下的加速度可以分解为两个方向
d
V
⃗
d
t
=
d
V
d
t
τ
⃗
+
V
2
R
T
n
⃗
\frac{d\vec{V}}{dt} = \frac{dV}{dt} \vec{\tau} + \frac{V^2}{R_T} \vec{n}
dtdV=dtdVτ+RTV2n
其中第一项为切向加速度,第二项为法向加速度
结合气压梯度力和地转偏向力
d
V
d
t
=
−
∂
ϕ
∂
s
V
2
R
T
=
−
∂
ϕ
∂
n
−
f
V
\begin{align} \frac{dV}{dt} &= - \frac{\partial \phi}{\partial s} \\ \frac{V^2}{R_T} &= -\frac{\partial \phi}{\partial n} - fV \\ \end{align}
dtdVRTV2=−∂s∂ϕ=−∂n∂ϕ−fV
地转风
地转偏向力与气压梯度力平衡,即地转平衡,风沿着等压线运动
−
∂
ϕ
∂
n
−
f
V
g
=
0
-\frac{\partial \phi}{\partial n} - fV_g = 0
−∂n∂ϕ−fVg=0
在p坐标系下地转风矢量表示
V
⃗
=
−
1
f
∇
ϕ
×
k
⃗
=
−
1
ρ
f
∇
p
×
k
⃗
\vec{V} = -\frac{1}{f} \nabla \phi \times \vec{k} = -\frac{1}{\rho f} \nabla p \times \vec{k}
V=−f1∇ϕ×k=−ρf1∇p×k
对于散度
∇
⋅
V
g
⃗
=
∇
⋅
(
1
f
k
⃗
×
∇
ϕ
)
=
∇
⋅
(
−
1
f
∂
ϕ
∂
y
i
⃗
+
1
f
∂
ϕ
∂
x
j
⃗
)
=
0
\nabla \cdot \vec{V_g} = \nabla \cdot (\frac{1}{f} \vec{k} \times \nabla \phi) = \nabla \cdot (-\frac{1}{f} \frac{\partial \phi}{\partial y} \vec{i} + \frac{1}{f} \frac{\partial \phi}{\partial x} \vec{j}) = 0
∇⋅Vg=∇⋅(f1k×∇ϕ)=∇⋅(−f1∂y∂ϕi+f1∂x∂ϕj)=0
可得地转风散度为0
一般用于中纬度地区大尺度天气系统,因为中纬度地区地转偏向力适中,对于低纬度地区,无法用地转风分析,需要借助其他方法如流函数
地转风不考虑摩擦力,加速度和垂直速度,对于曲率半径千公里量级可以近似为地转风
梯度风
上边提到的方程两端均考虑 − V 2 R T − ∂ ϕ ∂ n − f V = 0 -\frac{V^2}{R_T} - \frac{\partial \phi}{\partial n} - fV = 0 −RTV2−∂n∂ϕ−fV=0
解此一元二次方程
V
f
=
−
R
T
2
f
±
R
T
2
f
2
−
4
R
T
∂
ϕ
∂
n
V_f = \frac{-R_T}{2}f \pm \frac{R_T}{2} \sqrt{f^2 - \frac{4}{R_T} \frac{\partial \phi}{\partial n}}
Vf=2−RTf±2RTf2−RT4∂n∂ϕ
对气旋和反气旋分别分析,可得都应当取正号
高压中心附近气压梯度小,边缘气压梯度大(公式里根号内值为0),低压中心附近气压梯度力大
将梯度风方程与地转风方程联立可得
V
g
V
f
=
1
+
V
f
f
R
T
\frac{V_g}{V_f} = 1+ \frac{V_f}{fR_T}
VfVg=1+fRTVf
或
V
f
−
V
g
=
−
V
f
2
f
R
T
V_f - V_g = - \frac{V_f^2}{fR_T}
Vf−Vg=−fRTVf2
其中
V
g
V_g
Vg 为地转风,可得到中纬度气旋环流中,地转风比梯度风大,反气旋中,梯度风比地转风更大,两者相差并不大,但对于热带气旋,两者的差较大,因此地转关系不适用,改用梯度风分析
惯性流与旋衡流(选学)
惯性流:忽略气压梯度力,只考虑惯性离心力和地转偏向力的平衡
旋衡流:忽略地转偏向力,只考虑气压梯度力和惯性离心力的平衡,一般用于中小尺度天气系统如龙卷等
浅薄与深厚的高低压系统
- 深厚:热高压、冷低压
- 浅薄:热低压、冷高压
可以用静力平衡方程解释
∂
p
∂
z
=
−
ρ
g
\frac{\partial p}{\partial z} = -\rho g
∂z∂p=−ρg
暖空气膨胀,密度减小,相同的气压值减小量,对应高度的增量会更大,因此会形成暖高压
热成风
热成风并非为真实的风,而是指地转风随高度的变化
关于西风的形成:因为南北空气受热不匀,导致两等压面之间的厚度发生变化,南北形成气压梯度力,气压梯度力与地转偏向力平衡后,形成西风,且对流层内海拔越高,斜压性越强,气压梯度越大,西风越强,可以认为在对流层内有西风热成风
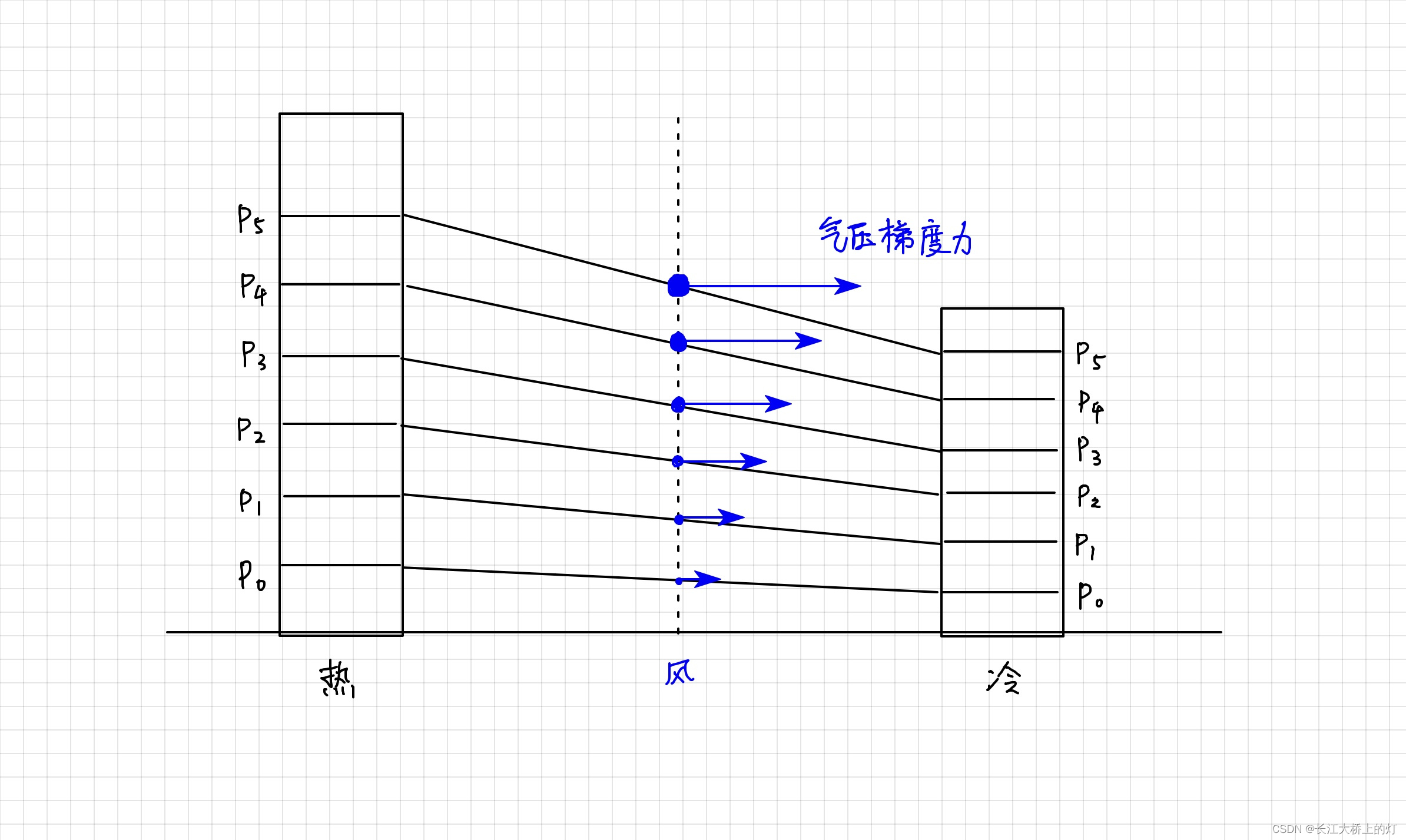
其中等压面厚度与温度的关系
h
=
z
1
−
z
0
=
−
∫
p
0
p
1
R
T
p
g
d
p
=
R
g
T
ˉ
ln
p
0
p
1
h = z_1 -z_0 = -\int_{p_0}^{p_1} \frac{RT}{pg} dp = \frac{R}{g} \bar{T} \ln \frac{p_0}{p_1}
h=z1−z0=−∫p0p1pgRTdp=gRTˉlnp1p0
其中
p
0
>
p
1
p_0 > p_1
p0>p1,
T
ˉ
\bar{T}
Tˉ 表示该气层的平均温度
可得热成风表达式
V
T
⃗
=
R
f
k
⃗
×
∇
h
=
R
f
ln
p
0
p
1
k
⃗
×
∇
T
ˉ
\vec{V_T} = \frac{R}{f} \vec{k} \times \nabla h = \frac{R}{f} \ln \frac{p_0}{p_1} \vec{k} \times \nabla \bar{T}
VT=fRk×∇h=fRlnp1p0k×∇Tˉ
借助热成风分析暖平流与冷平流的方法
- 风向随高度逆转为冷平流
- 风向随高度顺转为暖平流
可画图分析

当风向随高度逆转,热成风水平向东,可得到南边暖,北边冷,此时形成的平流为冷平流,暖平流同理
中纬度地区温压场
假设初始状态下,等温线平直,南暖北冷,近地面高度存在高低压中心,根据热成风原理,该场中的热成风应当为西风,则随着高度的增加,将热成风与近地面地转风叠加,可得高空地转风,原先的高低压中心会在高空转变为波状的脊、槽,且槽和脊之间的等压线不与等温线平行,形成暖平流或冷平流,导致原有平直的等温线不能维持,形成暖舌和冷舌
可见温度平流使得等温线(热成风)弯曲且变化落后于气压场变化
同时当等温线发生弯曲后,热成风方向发生变化,通过绘图分析可得,随高度增加,高空槽、脊会不断向西偏移

借助热成风也可以解释,暖性高压系统非常深厚(热成风与低层地转风同向),冷性高压系统比较浅薄(热成风与低层地转风反向),同理,冷低压非常深厚,暖低压比较浅薄
正压大气与斜压大气
- 正压大气:大气密度仅与气压有关,热成风等于0,等压面与等温面、等密度面平行
- 斜压大气:大气密度与气压和温度都有关,热成风不等于0,等压面与等温面相交
地转偏差
地转偏差描述实际风向与地转风之间的偏差
D
⃗
=
V
⃗
−
V
g
⃗
\vec{D} = \vec{V} - \vec{V_g}
D=V−Vg
摩擦层中的地转偏差
地转偏差方向在摩擦力方向的右侧,这使得低压系统低层辐合,高压系统低层辐散
D
⃗
=
V
⃗
−
V
g
⃗
=
−
1
f
k
⃗
×
F
⃗
\vec{D} = \vec{V} -\vec{V_g} = -\frac{1}{f}\vec{k} \times \vec{F}
D=V−Vg=−f1k×F
自由大气加速度引起的地转偏差
自由大气中的摩擦力很小,可以忽略,当气压梯度力与地转偏向力不平衡时,会产生加速度
d
V
⃗
d
t
=
f
k
⃗
×
V
g
⃗
−
f
k
⃗
×
V
⃗
=
−
f
k
⃗
×
D
⃗
\frac{d\vec{V}}{dt} = f\vec{k} \times \vec{V_g} - f\vec{k} \times \vec{V} = -f \vec{k} \times \vec{D}
dtdV=fk×Vg−fk×V=−fk×D
地转偏差指向加速度左侧
D
⃗
=
1
f
k
⃗
×
d
V
⃗
d
t
=
1
f
k
⃗
×
d
V
g
⃗
d
t
\vec{D} = \frac{1}{f} \vec{k} \times \frac{d\vec{V}}{dt} = \frac{1}{f} \vec{k} \times \frac{d\vec{V_g}}{dt}
D=f1k×dtdV=f1k×dtdVg
为了在天气图上定性分析地转偏差,将加速度在自然坐标系下展开为局地加速度和平流加速度
D
⃗
=
1
f
k
⃗
×
(
∂
V
g
⃗
∂
t
+
V
g
∂
V
g
⃗
∂
s
+
ω
∂
V
g
⃗
∂
p
)
=
D
1
⃗
+
D
2
⃗
+
D
3
⃗
\vec{D} = \frac{1}{f} \vec{k} \times (\frac{\partial \vec{V_g}}{\partial t} + V_g \frac{\partial \vec{V_g}}{\partial s} + \omega \frac{\partial \vec{V_g}}{\partial p}) = \vec{D_1}+\vec{D_2}+\vec{D_3}
D=f1k×(∂t∂Vg+Vg∂s∂Vg+ω∂p∂Vg)=D1+D2+D3
对于
D
1
D_1
D1 表示气压梯度力局地变化,导致气压梯度力与地转偏向力不平衡,引起的局地加速度
D
1
⃗
=
−
1
f
2
ρ
∇
(
∂
p
∂
t
)
=
−
9.8
f
2
∇
(
∂
H
∂
t
)
\vec{D_1} = -\frac{1}{f^2\rho} \nabla (\frac{\partial p}{\partial t}) = -\frac{9.8}{f^2} \nabla (\frac{\partial H}{\partial t})
D1=−f2ρ1∇(∂t∂p)=−f29.8∇(∂t∂H)
在地面天气分析中,使用三小时变压来分析,变压梯度正中心,地转偏差为辐散,对应下沉气流
对于
D
2
D_2
D2 可以分解为法向和切向加速度引起的偏差
D
2
⃗
=
1
f
k
⃗
×
(
V
g
∂
V
g
∂
s
τ
⃗
+
V
g
2
n
⃗
R
)
=
1
f
V
g
∂
V
g
∂
s
n
⃗
−
1
f
V
g
2
R
τ
⃗
=
D
2
n
⃗
+
D
2
s
⃗
\vec{D_2} = \frac{1}{f} \vec{k} \times (V_g \frac{\partial V_g}{\partial s} \vec{\tau} + V_g^2 \frac{\vec{n}}{R}) = \frac{1}{f} V_g \frac{\partial V_g}{\partial s} \vec{n} - \frac{1}{f} \frac{V_g^2}{R} \vec{\tau} = \vec{D_{2n}} + \vec{D_{2s}}
D2=f1k×(Vg∂s∂Vgτ+Vg2Rn)=f1Vg∂s∂Vgn−f1RVg2τ=D2n+D2s
在高空天气分析中
- 切向加速度:等压线汇合,地转风产生正向加速度,因为地转偏差指向加速度的左侧,非地转风法向穿过等压线指向低压,反之同理
- 法向加速度:槽区,运动加速度法向正向,地转偏差指向加速度的左侧,对应运动切向反向,非地转风与地转风反向,脊区,非地转风与地转风同向;槽前脊后,高空辐散,对应地面上升运动补偿,地面减压,槽后脊前,高空辐合,对应下沉运动,地面加压
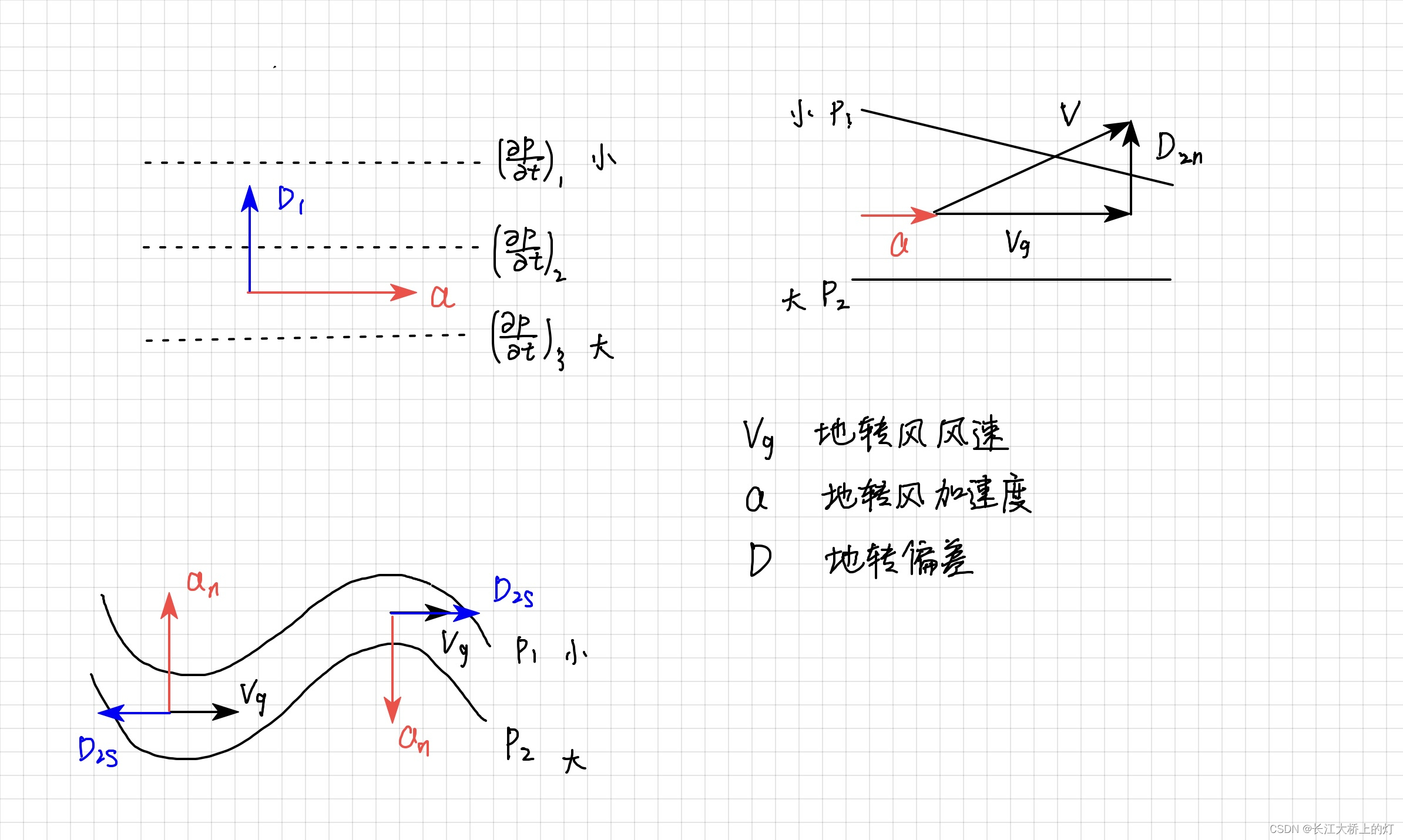
对流加速度表示的地转偏差,在大气垂直运动较强时考虑,将水平风场近似用地转风代入,同时代入热成风公式可得到
D
3
⃗
=
ω
R
f
2
p
∇
T
\vec{D_3} = \frac{\omega R}{f^2p} \nabla T
D3=f2pωR∇T
当大气盛行上升运动,
ω
<
0
\omega<0
ω<0 偏差指向温度下降的方向

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








