二、气团与锋
前言
本课程使用教材为《天气学原理和方法(第四版)》(气象出版社),文章根据课堂笔记和教材内容整理订正编写,文章内容如有错误,请指正。
系列文章链接如下:
大气运动基本特征
气团与锋
气旋与反气旋
天气形势与天气要素预报
大气环流
20世纪20年代挪威学派以温度变化(气团与锋的概念提出)总结出天气分析和预报的规则
文章目录
气团与锋基本概念
气团
气象要素分布比较均匀的大范围空气团
尺度上,水平方向数千公里,垂直范围再几公里到整个对流层
气团内控制的天气现象基本相同,温湿度分布均匀,逐日变化小但日变化很大
气团形成的基本条件:下垫面性质均匀广阔,环流稳定
气团会发生变性,即物理性质发生改变,一般来说,冷气团到达暖的地区变性较快(低层变暖容易发生对流),暖气团到达冷的地区变性较慢。潮湿气团变干缓慢而干燥气团变潮湿更快
气团分类:北极气团、极地气团(分为大陆性和海洋性)、热带气团(分为大陆性和海洋性)、赤道气团
锋
两气团相遇形成锋
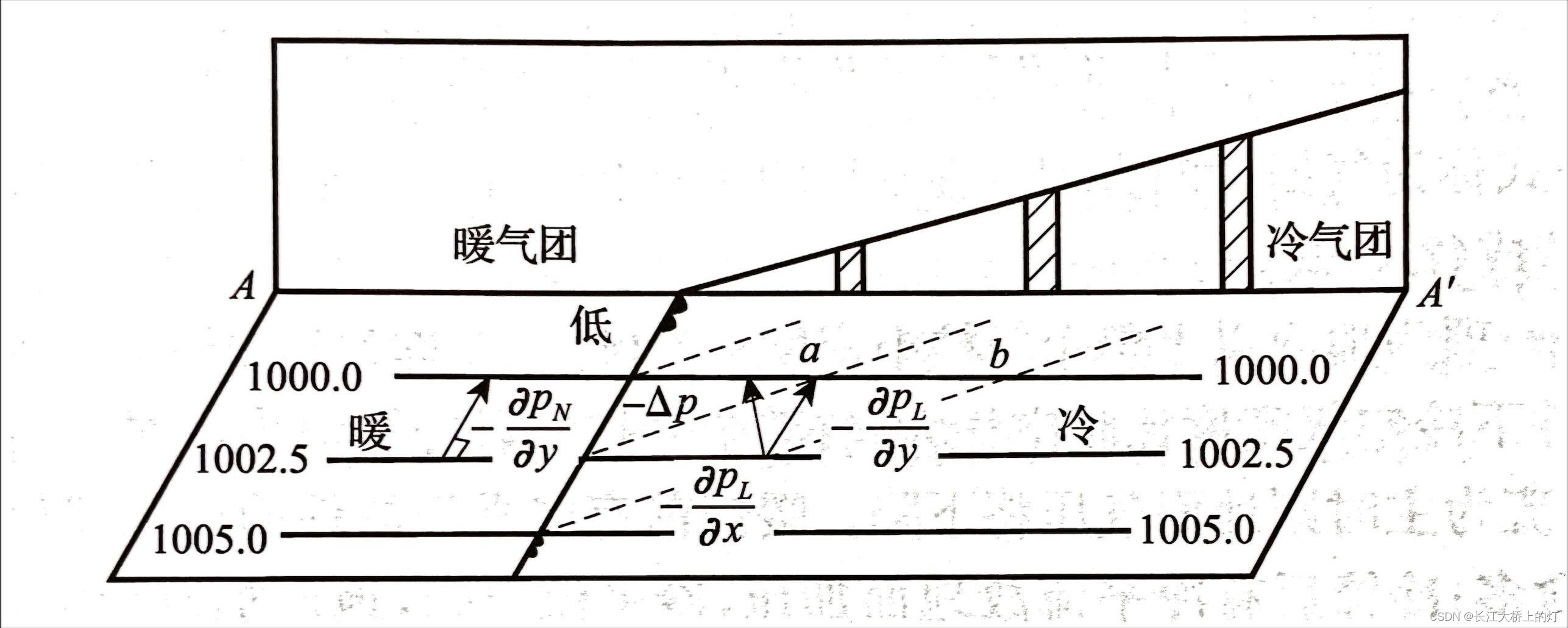
对锋进行零级近似可以看作锋面,进行一级近似可看作锋区(锋面与高空某一平面相交的区域,高空锋面宽度会增加,可以用质量守恒解释)
锋面坡度
零级近似的Margules公式
零级近似下,锋面上等压线连续,但等压线不光滑,发生转向(一级不连续),等温线在锋面上间断(零级不连续)
一级近似下,锋区内气压二级不连续,气温一级不连续
建立零级近似模型,设锋面与
y
y
y 轴平行,坡度为
α
\alpha
α,可以得到锋面处
p
l
=
p
n
p_l = p_n
pl=pn 可以进行全微分并相减
d
p
l
−
d
p
n
=
0
dp_l - dp_n = 0
dpl−dpn=0
得到
tan
α
=
d
z
d
x
=
−
∂
p
l
∂
x
−
∂
p
n
∂
x
∂
p
l
∂
z
−
∂
p
n
∂
z
\tan \alpha = \frac{dz}{dx} =- \frac{\frac{\partial p_l}{\partial x} - \frac{\partial p_n}{\partial x}}{\frac{\partial p_l}{\partial z}-\frac{\partial p_n}{\partial z}}
tanα=dxdz=−∂z∂pl−∂z∂pn∂x∂pl−∂x∂pn
将地转风公式与静力平衡方程、理想气体状态方程代入,得到Margules公式
tan
α
=
f
g
T
n
V
g
l
−
T
l
V
g
n
T
n
−
T
l
=
f
g
T
m
Δ
V
g
Δ
T
+
f
g
V
g
m
≈
f
g
T
m
Δ
V
g
Δ
T
\tan \alpha = \frac{f}{g} \frac{T_nV_{gl} - T_lV_{gn}}{T_n-T_l} = \frac{f}{g} T_m \frac{\Delta V_g}{\Delta T} + \frac{f}{g} V_{gm} \approx \frac{f}{g} T_m \frac{\Delta V_g}{\Delta T}
tanα=gfTn−TlTnVgl−TlVgn=gfTmΔTΔVg+gfVgm≈gfTmΔTΔVg
其中
T
m
=
T
n
+
T
l
2
,
V
g
m
=
V
g
n
+
V
g
l
2
,
Δ
V
g
=
V
g
l
−
V
g
n
,
Δ
T
=
T
n
−
T
l
T_m = \frac{T_n+T_l}{2}, V_{gm} = \frac{V_{gn}+V_{gl}}{2},\Delta V_g = V_{gl} - V_{gn},\Delta T =T_n - T_l
Tm=2Tn+Tl,Vgm=2Vgn+Vgl,ΔVg=Vgl−Vgn,ΔT=Tn−Tl , 注意
V
g
l
,
V
g
n
V_{gl},V_{gn}
Vgl,Vgn 分别表示冷暖气团中地转风速度在锋线上的分量
锋面两侧速度反向,速度差大于速度和,所以计算忽略第二项,进行近似
根据公式可以得到,锋面坡度与锋两侧温度差成反比,与风速差成正比,与锋面两侧平均温度成正比
当锋面附近气流曲率较大时,地转风公式将不适用,需要将锋面坡度公式与梯度风公式联立
tan
α
≈
(
f
+
2
k
T
V
f
ˉ
)
T
m
g
Δ
V
f
Δ
T
\tan \alpha \approx (f + 2k_T\bar{V_f}) \frac{T_m}{g} \frac{\Delta V_f}{\Delta T}
tanα≈(f+2kTVfˉ)gTmΔTΔVf
其中
k
T
=
1
R
T
k_T = \frac{1}{R_T}
kT=RT1
V
f
ˉ
\bar{V_f}
Vfˉ 锋线两侧梯度风的平均值,
Δ
V
f
\Delta V_f
ΔVf 为锋线两侧梯度风差值
一级近似
锋区宽度在不同高度不同,因此锋区与暖空气和冷空气之间的夹角不同
对于锋区和冷空气部分
tan
α
=
−
∂
2
p
l
∂
x
2
−
∂
2
p
f
∂
x
2
∂
2
p
l
∂
x
∂
z
−
∂
2
p
f
∂
x
∂
z
\tan \alpha = -\frac{\frac{\partial^2 p_l}{\partial x^2}- \frac{\partial ^2 p_f}{\partial x^2}}{\frac{\partial ^2 p_l}{\partial x\partial z}- \frac{\partial ^2 p_f}{\partial x\partial z}}
tanα=−∂x∂z∂2pl−∂x∂z∂2pf∂x2∂2pl−∂x2∂2pf
与零级近似同理可用公式进行适当代入
锋区与暖空气部分同理
一级近似公式化简较难,一般一级近似使用比较少
锋的分类
- 根据移动分类:冷锋、暖锋、准静止锋、锢囚锋
关于锢囚锋:锢囚锋分为冷性锢囚锋、中性锢囚锋和暖性锢囚锋,形成锢囚锋主要原因是冷锋追上暖锋,导致中部暖气团被完全抬升至空中,若将高空等温线向水平面投影,可以看到暖舌结构,如图为冷式锢囚锋的示意图
- 根据高度分类:对流层锋、地面锋、高空锋
- 根据地理位置:冰洋锋、极锋、副热带锋
锋的运动学性质
以天气尺度为背景,锋的各种梯度表现为各种要素的不连续,大体上有以下规律
- 锋区附近温度梯度大
- 水平方向上分析,锋线附近等压线有明显弯曲并弯曲方向指向高压
如图为暖锋锋面模型,由于冷空气密度大于暖空气,所以冷区一侧地面气压比暖区一侧要大,这也是天气图上锋线附近等压线呈现明显弯曲的原因
- 冷锋锋后有明显正变压,暖锋锋前有明显负变压,借助上图动态分析也可得到
- 水平方向上分析,锋线附近有气旋性风切变,即正相对涡度(自然坐标系下 ζ = V R − ∂ V ∂ n > 0 \zeta = \frac{V}{R} - \frac{\partial V}{\partial n}>0 ζ=RV−∂n∂V>0),根据此规律可以分析在气压场中是否具有形成锋的条件,简单来说,锋面可以形成于两高压之间,高压和低压之间(靠近高压处风大),不能形成于两低压之间。
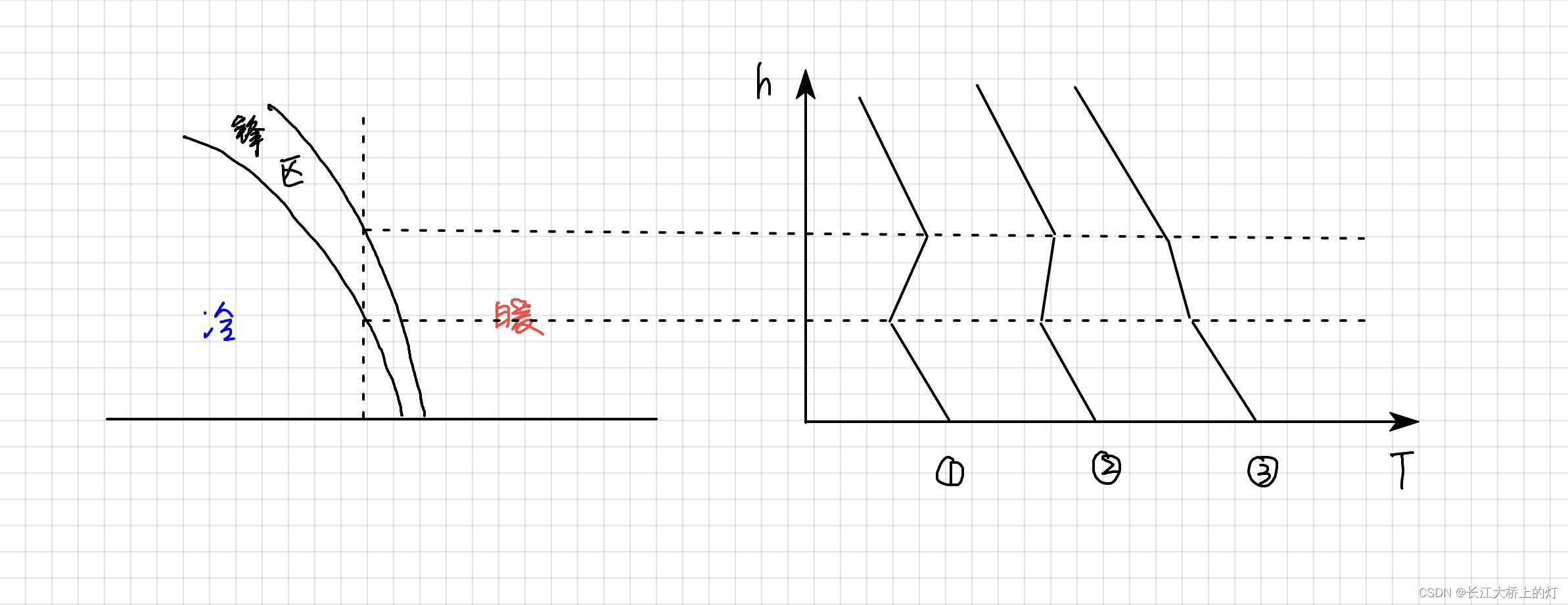
- 垂直方向上分析,锋区内温度递减率减少,位温递增率增加,大气稳定度增大,可能出现逆温
图中1、2、3分别表示锋区逆温,近似等温,温度递减率减小三种情况
- 锋区附近有明显的天气现象,对于中纬度较为湿润的地区,云覆盖增加,形成降水,对于干燥地区为阴天不一定形成降水,可能会有沙尘或吹雪天气
拓展:中纬度高空急流与锋区的关系
如图为一锋区,左侧为冷空气,右侧为暖空气,等温线高度不同,因此可得到锋区内温度垂直递减率减少,位温随高度增加而增加,锋区内大气更加稳定。根据热成风原理,右侧高温,左侧低温,会形成垂直平面向内的热成风。随着高度增加,垂直平面向内的地转风会增强,形成高空急流。当高度达到一定程度后,左侧进入平流层,温度随高度增加,右侧气柱膨胀,对流层顶高度更高,同一高度下还处于对流层,因此形成左热右冷的格局,热成风反向,高空急流随高度增加减弱。
锋面天气
引起锋附近垂直运动的因子
- 地面摩擦辐合上升
- 锋面移动产生的抬升
- 高空槽前后系统性上升和下降(结合第一章地转偏差)
- 冷暖平流引起的上升和下降
冷锋锋后坏天气——一型冷锋
高空槽在冷锋后,锋到达前天气晴好,锋后开始有降水,当700hpa高空槽经过后,降水减少,转为中云天气,500hpa高空槽经过后,逐渐转晴
冷锋锋前坏天气——二型冷锋
高空槽在冷锋前,高空槽后有下沉气流,高空冷平流强,抑制锋面附近云向锋面后发展,降水聚集在锋面附近或锋面前,且锋前暖空气强烈抬升,若暖空气不稳定,多形成积雨云和雷阵雨天气,若冷锋前后空气干燥,则锋前后均没有云,只有风沙或吹雪
两者区别在于降水区域不同,冷平流强度不同(二型更强),大气稳定性不同(一型更稳定)
暖锋降水分析
- 若暖锋低层辐合明显,700hpa高空有槽线,则暖锋前降水较大
- 若700hpa高空槽线在暖锋后很远,暖锋上空等高线有反气旋曲率,则降水在暖区发展
准静止锋降水分析
- 准静止锋降水较少的情况:多半在高压控制下,锋上暖空气较干燥,没有显著的云,锋下冷空气湿润并且沿着地形抬升形成层积云,在我国常见的有天山准静止锋
- 准静止锋降水较多的情况:锋上暖空气有较强的上升运动,雨区北界往往与700hpa切变线一致,我国常见的有江淮准静止锋
锢囚锋降水分析
锢囚锋的云由两个锋面的云合并形成,因此天气最恶劣的区域在锢囚锋附近。随着时间的推移,暖空气被抬升更高,云底高度变得更高,云也会变得更薄,锋下锢囚锋面上会有新的云发展起来。
锋面分析方法
前面提到的,锋面两侧气象要素的变化,可以作为分析锋面的依据
温度
锋面两侧会有一定的温差,但是近地面大气温度会受到辐射、水汽凝结、空气垂直运动、地形、海陆等多方面影响,会存在锋面两侧温差不明显的情况,即温度资料失去代表性,因此,只从有明显温差这一情况,也不能一定说明有锋面存在
露点
一般来说我国暖空气来自海上,较为湿润,冷空气较为干燥,在没有降水发生的条件下,露点能反映气团属性,能够分析锋面
气压与风
等压线通过锋面会有折角,且折角指向高压,锋面两侧有风向的气旋式切变,但是气旋式风切变并不能完全一定反映有锋面存在,需要结合具体情况综合考虑
变压
三小时变压分析:冷锋后有较强的正变压,暖锋前有较强的负变压,根据政府变压中心区域分布确定锋面
卫星云图分析
一般情况简单来说,锋面附近会有明显带状云系,长度可以达到数千公里,但宽度差异较大,具体问题需要分情况讨论,此处不展开
探空资料
锋面经过时,探空曲线上可以看到锋面逆温或温度递减率显著减小(用锋面结构很容易解释)
湿度上看,一般来说锋面逆温,上层湿润,下层干燥,可以借助湿度资料分析。
不过如果有降水,逆温层下湿度也较大;如果暖空气干燥,逆温层上方湿度较小,锋面逆温与下沉逆温不易区分,需要前面时次的探空曲线资料,若逆温层下降温,逆温层上升温、等温或降温不大,可以初步分析为锋面逆温
高空测风资料
高空测风资料,一般用单站风廓线(profile)数据,其分析规律是
- 热成风方向大致代表锋的走向
- 最大热成风位置确定锋的高度
- 根据风随高度变化确定锋的性质
- 原点与代表锋面的热成风的垂线代表锋的移向和速度
在填图后的高空天气图上分析,等温线密集处为高空锋区,锋的走向与等温线平行,地面锋面在高空锋区偏暖的一侧
单站测风图阅读:
类似极坐标,坐标平面上一点表示风的去向,其中该点距离原点的距离表示风的大小,两个高度的风的连线表示热成风详见如下实例分析
实例分析:单站测风结果分析高空锋面与降水
对于图中第一个测风图,在较低高度范围内,随着高度的增加,风向逐渐逆转,根据热成风和冷暖平流的规律,可得低空冷平流。当到达一定高度后,风向随高度顺转,可得高空为暖平流。因此,低空温度会降低,而高空温度会升高。因此,大气稳定度增加,不容易发生降水。第二个测风图则相反,更容易发生降水。对于图中第一个测风图,在2.5km到3km的高度区间内,热成风最大,风向明显逆转,为冷平流,因此该区间内对应冷锋的高度,且锋面向东南方向移动。(仅为初步分析,此案例在锋面分析上并不具有代表性,但规律类似)
综合实例分析:美国麦迪逊(Madison)某次冷锋过境天气过程
根据左上方的图,可得到,天气系统经过前,温度较高,温度露点差较大(气团干燥);经过后,温度显著下降且温度露点差减少(气团湿润),表明干热气团由湿冷气团替代,即冷锋过境,同时还能观察到明显的风切变
根据右上方的图,图中实线为等位温线,虚线为等风速线,阴影区为等位温线密集区,其中高处等位温线密集区为平流层,可以发现图中等位温线密集区向低海拔处延申,可以确定该区域温度递减率相较于同高度的其他区域更小,为冷锋锋区,且锋前有明显的急流。
在近似绝热过程中,空气沿着等位温线运动,会发现平流层空气会沿着等位温线进入对流层,此类现象带来的影响为对流层臭氧污染(平流层臭氧沿着等位温线进入到对流层)。
锋生与锋消
锋生:密度不连续的形成过程或已有锋面之后温度与位温的水平梯度增大
锋消:与锋生相反
锋生与锋消的运动学特征
定义
n
⃗
\vec{n}
n 方向上的温度梯度
T
n
=
∂
T
∂
n
T_n = \frac{\partial T}{\partial n}
Tn=∂n∂T
定义锋生函数
F
=
d
d
t
T
n
F = \frac{d}{dt} T_n
F=dtdTn
锋生线上温度梯度加大且加大得最快,即
F
>
0
,
∂
F
∂
n
=
0
,
∂
2
F
∂
n
2
<
0
F > 0 ,\frac{\partial F}{\partial n} = 0,\frac{\partial ^2 F }{\partial n^2} < 0
F>0,∂n∂F=0,∂n2∂2F<0
对锋生函数进行分析,水平方向上只考虑温度增加的方向,即水平一维
应用局地变化与平流变化的关系分析
F
=
∂
T
n
∂
t
+
V
∂
T
n
∂
n
+
ω
∂
T
n
∂
p
=
∂
∂
n
(
d
T
d
t
−
V
n
∂
T
∂
n
−
ω
∂
T
∂
p
)
+
V
n
∂
∂
n
∂
T
∂
n
+
ω
∂
∂
p
∂
T
∂
n
\begin{align*} F &= \frac{\partial T_n}{\partial t} + V \frac{\partial T_n}{\partial n} + \omega \frac{\partial T_n}{\partial p}\\ &= \frac{\partial }{\partial n} (\frac{dT}{dt} -V_n \frac{\partial T}{\partial n} -\omega \frac{\partial T}{\partial p}) + V_n \frac{\partial }{\partial n}\frac{\partial T}{\partial n} +\omega \frac{\partial }{\partial p}\frac{\partial T}{\partial n} \\ \end{align*}
F=∂t∂Tn+V∂n∂Tn+ω∂p∂Tn=∂n∂(dtdT−Vn∂n∂T−ω∂p∂T)+Vn∂n∂∂n∂T+ω∂p∂∂n∂T
将表达式展开,部分项抵消
应用能量守恒方程
d
Q
=
c
p
d
T
−
R
T
p
d
p
dQ = c_pdT - \frac{RT}{p} dp
dQ=cpdT−pRTdp 代入得到
F
=
∂
∂
n
(
1
c
p
d
Q
d
t
+
α
c
p
ω
)
−
∂
V
n
∂
n
∂
T
∂
n
−
∂
ω
∂
n
∂
T
∂
p
F = \frac{\partial }{\partial n} (\frac{1}{c_p} \frac{dQ}{dt} + \frac{\alpha}{c_p} \omega) -\frac{\partial V_n}{\partial n} \frac{\partial T}{\partial n} -\frac{\partial \omega}{\partial n}\frac{\partial T}{\partial p}
F=∂n∂(cp1dtdQ+cpαω)−∂n∂Vn∂n∂T−∂n∂ω∂p∂T
最终化简可得到三项
F
=
1
c
p
∂
∂
n
(
d
Q
d
t
)
−
∂
V
n
∂
n
∂
T
∂
n
+
σ
p
∂
ω
∂
n
F = \frac{1}{c_p} \frac{\partial }{\partial n}(\frac{dQ}{dt}) - \frac{\partial V_n}{\partial n} \frac{\partial T}{\partial n} + \sigma_p \frac{\partial \omega}{\partial n}
F=cp1∂n∂(dtdQ)−∂n∂Vn∂n∂T+σp∂n∂ω
其中
σ
p
=
α
c
p
−
∂
T
∂
p
\sigma_p = \frac{\alpha}{c_p} - \frac{\partial T}{\partial p}
σp=cpα−∂p∂T 表示大气稳定度
分别分析可得
- 非绝热加热项:冷空气变暖或暖空气变冷,使得锋面两侧温度梯度减小,锋消
- 水平辐合辐散项:沿着温度梯度正方向(温度上升的方向),空气速度辐合,等温线更密集,温度梯度增加,锋生,反之锋消。
- 稳定度与垂直运动项:对于稳定大气(空气抬升过程中没有发生水汽的相变, σ p > 0 \sigma_p > 0 σp>0 ),冷锋上山,暖空气一侧抬升冷却,冷空气一侧没有很大变化( ∂ ω ∂ n < 0 \frac{\partial \omega}{\partial n} < 0 ∂n∂ω<0 ),因此水平方向温度梯度减小,锋消;冷锋下山,冷空气一侧下沉增温,暖空气一侧变化不大,温度梯度减小,锋消。对于不稳定大气,冷锋上山,暖空气一侧抬升凝结释放潜热,温度梯度增加,锋生;冷锋下山,冷暖空气快速交汇,形成强对流,雷暴云形成后形成下沉气流,下方为雷暴冷高压,导致温度梯度加大,锋生。即稳定大气冷锋上山下山均锋消,不稳定大气均锋生
在对流层低层,水平运动是锋生的主要因子,对流层中层水平运动和垂直运动同样重要,对流层高层,水平汇合是重要因子
我国主要锋生锋消带
锋生带:北方锋生带为河西走廊到东北地区(北纬40-50度),南方锋生带为华南到长江流域(北纬20-30度),我国的锋生带满足的锋生条件:
- 冷锋锋生:温度槽落后于高度槽,槽后有冷平流,地面上冷锋产生于低压槽内或冷高压前部
- 暖锋锋生:高空850hpa、700hpa有暖式风切变,有很强的暖平流,地面上有西南倒槽
锋消带:青藏高原以东北纬30~40度为主要锋消带,主要原因:
- 位于高原东侧,下沉气流
- 位于东亚大槽后,盛行下沉气流
- 夏季受到副热带高压控制
我国锋面活动特点
- 冷锋最多,全年都可以产生
- 暖锋不会单独产生,一般与冷锋一起产生于锋面气旋
- 主要准静止锋有江淮准静止锋和云贵准静止锋
- 锢囚锋主要有河套锢囚锋、大巴山锢囚锋和东北锢囚锋





























 8726
8726

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








